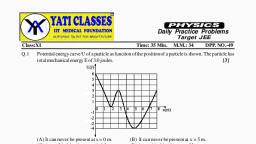
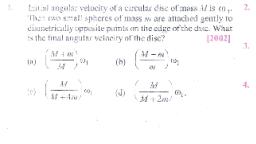Page 1 :
MATHEMATICS, , Daily Practice Problems, , Class:XI (Phase-1), Q.1, , Q.2, , Target JEE, Time: 24 Min. Discussion Date: 03-04/08/2015 M.M.: 28, Dpp. No.-51, , [SINGLE CORRECT CHOICE TYPE], [6 × 3 = 18], 2, 3, 10, Consider the ten numbers ar, ar , ar , .......... ar ., If their sum is 18 and the sum of their reciprocals is 6 then the product of these ten numbers, is, (A) 324, (B) 343, (C) 243, (D) 729, ,  1, 7 , , , If cos     = , where 0 <  <, then the value of tan     is equal to, 2, 18  3, 18 , , , , (A), , 2 2 3, 1 2 6, , (B), , 2 2 3, 1 3 6, , (C), , 2 2 3, 1 6 2, , (D), , 2 2 3, 1 2 6, , 1, , a  R – {0}, such that f (3) > 0 and f (2)  0. If  and  are the, a, roots of equation f (x) = 0 then the value of 2 + 2 is equal to, (A) greater than 11, (B) less than 5, (C) 5, (D) depends upon 'a' and 'a' can not be determined., , Q.3, , Consider f (x) = x2 – 3x + a +, , Q.4, ,  , Let f (x) = 2 cosec 2x + sec x + cosec x, then the minimum value of f (x) for x   0,  is,  2, , 1, 2 1, , (A), Q.5, , 2, 2 1, , (C), , 2, 2 1, , (D), , Consider the series r2 + r4 + r6 + r8 + r10 + ....... . The third term is 16 times the fifth term., The sum of the series is, (A), , Q.6, , 1, 2 1, , (B), , 1, 4, , (B), , 1, 3, , (C), , 1, 2, , (D), , 4, 3, , If the equations p x2 + q x + r = 0 and r x2 + q x + p = 0 (p  r  0), have a negative common root, then the value of (p – q + r) is equal to, (A) –1, (B) 0, (C) 1, (D) 2, , Q.7, , [INTEGER TYPE], [2 × 5 = 10], 2, If M and m are maximum and minimum value of f (x) = cos x – 4 cos x + 7, x  R, respectively then find (M – m)., , Q.8, , Find the sum of all possible values of x satisfying the equation, , , , x 2  4 x  4 = (log2 9) log3 5, ,  log, , , , 25 256, , PAGE # 1

Page 2 :
MATHEMATICS, , Daily Practice Problems, , Class:XI (Phase-1), , Target JEE, Time: 24 Min. Discussion Date: 05-06/08/2015 M.M.: 26, Dpp. No.-52, [SINGLE CORRECT CHOICE TYPE], , Q.1, , , , (B) 100, , (C) 5050, , (D) 10, , cot 25º  cot 55º cot 55º  cot 100º cot 100º  cot 25º, +, +, is equal to, tan 25º  tan 55º tan 55º  tan 100º tan 100º  tan 25º, (B) 1, (C) 2, (D) 3, , The value of expression, (A) 0, , Q.3, , , , z, If x = 500, y = 100 and z = 5050, then the value of log xyz x 1  log x yz  is equal to, , (A) 500, Q.2, , [7 × 3 = 21], , If ,  are the roots of the equation x2 + px – r = 0 and, , , , 3 are the roots of the equation, 3, , x2 + qx – r = 0, then r equals, (A), , 3, (p – 3q) (3p + q), 8, , (B), , 3, (p + 3q) (3p – q), 8, , (C), , 3, (3p – q) (p – 3q), 64, , (D), , 3, (3q – p) (p – q), 64, , Q.4, , Let M denotes the maximum value of f(x) = sin2x – 4sin x + 10 and m denotes the minimum value of, f(x) = 4sec2x + 36cosec2x – 14, then (m – M) equals, (A) 15, (B) 25, (C) 35, (D) 45, , Q.5, , A polynomial P(x) = x2 + ax + b yields a remainder 2 upon a division by x – 1 and a remainder of, 1 upon division by x – 2, then the value of P(3) is, (A) 0, (B) 2, (C) 3, (D) 4, , Q.6, , Let x, |x – 1| and |x + 1| be the first three terms of a G.P. then sum of the series, 1, 1, 1, , , + ……  is equal to, x | x 1 | | x  1 |, (A) 9, , Q.7, , (B), , (C) 3, , (D) 6, , If roots of equation 8x3 – 14x2 + 7x – 1 = 0 are in geometric progression, then roots are, (A) 3, 6, 8, , Q.8, , 9, 2, , (B) 1, 2, 4, ,  , , If N = antilog7 log3 antilog, , (C) 2, 4, 8, , [INTEGER TYPE], 3, , log3 81 , then log3N, , (D) 1,, , 1 1, ,, 2 4, , [1 × 5 = 5], lies between two successive integers, , a and b. Find (a + b)., , PAGE # 2