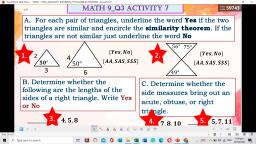
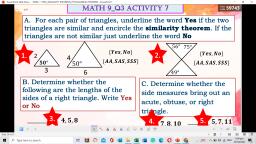
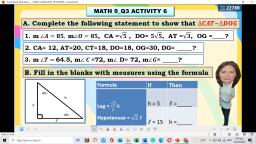
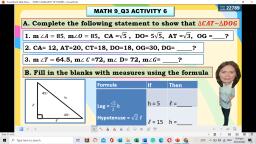
Page 2 :
Introductory Message, For the facilitator:, This module was collaboratively designed, developed and evaluated by the, Development and Quality Assurance Teams of SDO TAPAT to assist you in helping, the learners meet the standards set by the K to 12 Curriculum while overcoming, their personal, social, and economic constraints in schooling., As a facilitator, you are expected to orient the learners on how to use this module., You also need to keep track of the learners' progress while allowing them to manage, their own learning. Furthermore, you are expected to encourage and assist the, learners as they do the tasks included in the module., For the learner:, This module was designed to provide you with fun and meaningful opportunities for, guided and independent learning at your own pace and time. You will be enabled to, process the contents of the learning resource while being an active learner., The following are some reminders in using this module:, 1. Use the module with care. Do not put unnecessary mark/s on any part of the, module. Use a separate sheet of paper in answering the exercises., 2. Don’t forget to answer Let’s Try before moving on to the other activities, included in the module., 3. Read the instruction carefully before doing each task., 4. Observe honesty and integrity in doing the tasks and checking your answers., 5. Finish the task at hand before proceeding to the next., 6. Return this module to your teacher/facilitator once you are through with it., If you encounter any difficulty in answering the tasks in this module, do not, hesitate to consult your teacher or facilitator. Always bear in mind that you are, not alone., We hope that through this material, you will experience meaningful learning and, gain deep understanding of the relevant competencies. You can do it!
Page 3 :
Let’s Learn, This module was designed and written with you in mind. It is here to help you master, concepts about parallelogram. The scope of this module permits it to be used in many, different learning situations. The language used recognizes the diverse vocabulary, level of students. The lessons are arranged to follow the standard sequence of the, course. But the order in which you read them can be changed to correspond with, the textbook you are now using., The module contains lesson about properties of parallelogram., After going through this module, you are expected to:, 1. determine the conditions that make a quadrilateral a parallelogram;, 2. use properties to find measures of angles, sides and other quantities, involving parallelogram., , Let’s Try, Directions: Read each question carefully and solve if necessary. Choose the letter, of the correct answer and write it before the number., , 1. Two opposite angles of a parallelogram are _________., A. Supplementary, , B. Complementary, , C. Congruent, , D. Both right angles, , 2. Two opposite sides of a parallelogram are _________., A. Complementary, , B. Bisects each other C. Supplementary D. Congruent, , 3. Two consecutive angles of a parallelogram are __________., A. Supplementary, , B. Complementary, , C. Congruent, , D. Both right angles, , C. Congruent, , D. Both right angles, , 4. It bisects each other in a parallelogram., A. Supplementary, , B. Diagonals, , 5. When a diagonal bisects a parallelogram, it produces two __________ triangles., A. Congruent, , B. Complementary, , C. Right, , D. Supplementary
Page 4 :
Use the figure below to answer the following questions., , Given parallelogram WXYZ., 6. Find the measure of, A. 450, , Y., B. 550, , 7. Find the measure of, A. 450, , C. 650, , D. 1150, , C. 650, , D. 1150, , X., B. 550, , For items 8-10, find the value of x and y for which, , LOVE is a parallelogram., , 8., , A. 2, , B.6, , C. 8, , D. 12, , A. 𝑥 = 11, 𝑦 = 23, , B.𝑥 = 22, 𝑦 = 53, , C. 𝑥 = 23, 𝑦 = 11, , D. 𝑥 = 53, 𝑦 = 22, , A. 8, , B.9, , C. 10, , D. 11, , 9., , 10., , Alternatively, you may answer these questions online!, Scan the QR Code or use this link on your cellphone, laptop or desktop:, , https://forms.gle/8Cnmfzjz83fnUwEv9, Use proper capitalization to activate the link. You will see your score after, completing the test. Make sure to screenshot your work as a proof to your, teacher then write your score in the box. Make sure you are connected to, the internet!, , Put your, score here
Page 5 :
Lesson, , 1, , Properties of Parallelogram, , Let’s Recall, What Am I?, 1. I am a quadrilateral with one pair of parallel sides. What am I?, A. Square, , B. Trapezoid, , C. Rhombus, , D. Rectangle, , 2. I am a quadrilateral with two pairs of parallel sides. I have four right angles. I, have two pairs of opposite sides that are equal in length. What am I?, A. Rhombus, , B. Trapezoid, , C. Triangle, , D. Rectangle, , 3. I am a quadrilateral with two pairs of parallel sides. I have four right angles and, four equal side lengths. What am I?, A. Square, , B. Trapezoid, , C. Rhombus, , D. Rectangle, , 4. I am a quadrilateral with two pairs of parallel sides. I have four equal sides., What am I?, A. Kite, , B. Trapezoid, , C. Rhombus, , D. Rectangle, , 5. I am a quadrilateral with two pairs of equal adjacent sides. What am I?, A. Square, , B. Trapezoid, , C. Kite, , D. Rectangle, , Let’s Explore, PLOT, CONNECT, IDENTIFY, Given the following sets of ordered pair, plot it in a Cartesian plane. Connect the, points consecutively to form a quadrilateral. Identify the figure if it is a, parallelogram or not, then answer the questions that follows., , 1., 2., 3., 4., 5., , (0, 6), (0, 4), (4, 4), (4, 6), (-3, 3), (3, 3), (5, -4), (-5, -4), (-4, 1), (-4, 4), (-1, 3), (-1, 0), (0, 3), (-2, 0), (0, -5), (2, 0), (-3, 3), (-3, -3), (3, -3), (3, 3)
Page 6 :
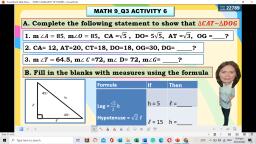
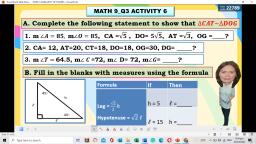
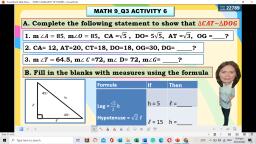
Processing questions:, , 1. In the figure formed, which are parallelograms? Why?, 2. In the figure formed, which are not parallelograms? Why?, , Let’s Elaborate, How will you determine if the figure is a parallelogram or not? By definition, a, parallelogram is a quadrilateral with two pairs of parallel sides. It has diagonals, that bisect a parallelogram into two equal triangles. The diagonals also bisect each, other. The opposite sides of parallelogram are parallel and congruent. The opposite, angles are congruent. The consecutive angles are supplementary., Example 1: Consider parallelogram DOVE., , Properties of Parallelogram, , Figure, For diagonal DV,, DEV ≅, VOD, , A. Each diagonal bisects the, parallelogram into two, congruent triangles., , B. The diagonals bisect each, other., , C. The opposite sides are, parallel and congruent., , D. The opposite angles are, congruent., , For diagonal EO, ODE ≅ EVO, , Diagonal DV bisects OE,, It means that EK ≅ OK, Diagonal OE bisects DV,, It means that DK ≅ VK, , DO ≅ EV, and, DE ≅ OV, , D≅ V, and, E≅ O
Page 7 :
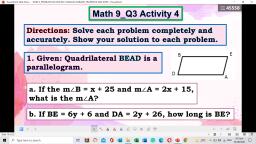
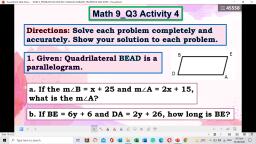
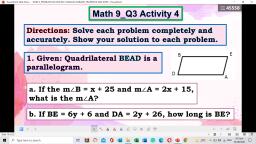
E. The consecutive angles are, supplementary., , m, m, m, m, , D+m, O+m, V+m, E+m, , O = 1800, V = 1800, E = 1800, D = 1800, , Use the properties of parallelogram in solving the following., Given: The diagonals of parallelogram CUTE intersect at G., , Example 2, If CU = 8 cm and CE = 5 cm, how long are sides ET and UT?, Solution:, Take note that CU and ET are opposite sides of parallelogram CUTE, so they have, equal length: CU = ET. Similarly, CE = UT., Thus, UT = 5 cm and ET = 8 cm., , Example 3, If EG = 6 cm and CG = 5.5 cm, how long are diagonals EU and CT?, Solution:, Since diagonals of parallelogram CUTE bisects each other, EU = 2(EG). Similarly,, CT = 2(CG)., Can you give the lengths of the diagonals?, EU = 2(EG), , CT = 2(CG), , EU = 2(6) cm, , CT = 2(5.5) cm, , EU = 12 cm, , CT = 11 cm, , Example 4, Find the value of x and y for which, , A., , MATH is a parallelogram., , B.
Page 8 :
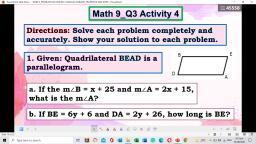
Solutions:, , A. The diagonals bisect each other., 6x – 12 = 3x, 3x – 12 = 0, Subtract 3x to each side, 3x = 12, Add 12 to each side, x=4, Divide each side by 3, 8y + 2 = 2y + 8, 6y + 2 = 8, 6y = 6, y=1, , Subtract 2y to each side, Subtract 2 to each side, Divide each side by 6, , B. For a quadrilateral to be a parallelogram, two pairs of opposite sides must, be congruent and parallel., 9y – 6 = 5y + 18, 4y – 6 = 18, 4y = 24, y=6, , Opposite sides are congruent, Subtract 5y to each side, Add 6 to each side, Divide each side by 4, , Example 5:, Find the value of x and y in parallelogram CURE., , A., , B., , Solutions:, , A. For a quadrilateral to be parallelogram, a pair of opposite angles must be, congruent., 5y – 15 = 3y + 45, 2y – 15 = 45, 2y = 60, y = 30, , Subtract 3y to each side, Add 15 to each side, Divide each side by 2, , B. The consecutive angles of a parallelogram are supplementary., 3x + 5 + 2x = 180, 5x + 5 = 180, 5x = 175, Subtract 5 to each side, x = 35, , Divide each side by 5, , Substitute the value of x to get the measure of two angles., C = 3x0 + 50, = 3(35)0 + 50, = 1050 + 50, = 1100, , U = 2x0, = 2(35)0, = 700
Page 9 :
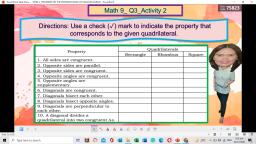
To find the measure of R, consider that R and U are supplementary angles., Thus,, R + U = 180, R + 70 = 180, Substitute the measure of U, R = 1100, Subtract 70 to each side, Note that, , C and, , R are congruent base on the properties of parallelogram., , To watch a video tutorial on Properties of Parallelogram,, by The Organic Chemistry Tutor,, visit this link: https://www.youtube.com/watch?v=t42sLuns4Qs, , Let’s Dig In, A. Determine whether the quadrilateral is a parallelogram based on the, following conditions. Put a √ beside each number if you agree with the, condition and × you disagree., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., , Both pairs of opposite sides are congruent., The diagonals are congruent., The consecutive angles are complementary., The opposite angles are congruent., All sides are congruent., Diagonals bisect each other., All angles are congruent., The diagonals are perpendicular., The opposite sides are parallel., The diagonal divides the quadrilateral into two congruent triangles., , B. Find the value of x and y that will make each quadrilateral a parallelogram., , 1., , 2., , 4., , 5., , 3.
Page 10 :
Let’s Remember, A parallelogram is a quadrilateral with two pairs of parallel sides., These are the properties of parallelogram:, 1., 2., 3., 4., 5., , Each diagonal divides the parallelogram into two congruent triangles., The diagonals bisect each other, The opposite sides of parallelogram are parallel and congruent., The opposite angles are congruent., Any two consecutive angles are supplementary., , Let’s Apply, Answer the following problems by applying the properties of parallelogram. Show, your solution., , 1. In the diagram above, TI and ME represent adjustable supports of a, basketball hoop. For what value of x is quadrilateral TIME a, parallelogram? What are the measures of both sides?, , 2. Using the same figure, if E is congruent to, x? What are the measures of both angles?, , I , what is the value of
Page 11 :
Let’s Evaluate, Directions: Read each question carefully and solve if necessary. Choose the letter, of the correct answer and write it before the number., , 1. The ________ of a parallelogram bisect each other., A. sides, , B. lines, , C. diagonals, , D. angles, , 2. A parallelogram has two consecutive angles that are __________., A. congruent, , B. both right angles, , C. supplementary D. complementary, , 3. A parallelogram has two pairs of _________ angles that are congruent., A. parallel, , B. opposite, , C. consecutive, , D. non consecutive, , 4. The pair of opposite sides of a parallelogram must be _________., A. congruent & parallel, , C. congruent & diagonal, , B. congruent & perpendicular, , D. congruent & intersecting, , 5. How many diagonals are there in a parallelogram?, A., , 2, , B., , 3, , C., , 4, , D., , 5, , Use the figure to answer the questions for nos. 6-10., , 6. If m E = 27x and m, parallelogram?, A., , I = 81, what is the value of x to make the quadrilateral a, , 2, , B., , 3, , C., , 4, , D., , 5, , D., , 9, , D., , 40, , 7. If EJ ≅ IJ, what is the value of y if EJ = 2y – 4 and IJ = y + 5?, A., , 1, , B., , 3, , C., , 7, , 8. In parallelogram MINE, MI ∥ EN, what is the measure of MI if EN = 20?, A., 9., , N and, , 10, , B., , C., , E are supplementary angles. The measure of, , E = (x – 6)0. What is the measure of, A., , 20, , 550, , B., , 650, , 550, , B., , 650, , N = (2x+3)0 and, , N?, C., , 10. Using the given in no. 9, what is the measure of, A., , 30, , C., , 1150, , D. 1250, , E?, 1150, , D. 1250
Page 12 :
Alternatively, you may answer these questions online!, Scan the QR Code or use this link on your cellphone, laptop or desktop:, , https://forms.gle/7tFBVjo6fuFcTTSS7, , Put your, score here, , Use proper capitalization to activate the link. You will see your score after, completing the test. Make sure to screenshot your work as a proof to your, teacher then write your score in the box. Make sure you are connected to, the internet!, , Let’s Extend, Directions: Find the value of x and y that will make each quadrilateral a, parallelogram hence find the measures of unknown angles/sides., , 1., , 2., , Alternatively, you may answer these questions online!, Scan the QR Code or use this link on your cellphone, laptop or desktop:, , https://forms.gle/49KKsTkMQNLM2Wy28, Use proper capitalization to activate the link. You will see your score after, completing the test. Make sure to screenshot your work as a proof to your, teacher then write your score in the box. Make sure you are connected to, the internet!, , Put your, score here
Page 13 :
References, Nivera, Gladys C., et. al., GRADE 9 MATHEMATICS (Patterns and Practicalities),, Salesiana Books, 2013, Oronce, Orlando A., et. al., E-MATH 9 (Work text in Mathematics), Rex Book Store,, 2015, MATHEMATICS GRADE 9, LEARNER’S MATERIAL, Department of Education, First, Edition, 2014