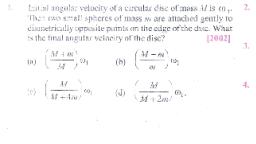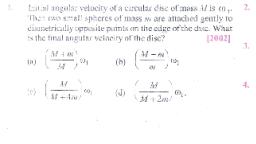Page 1 :
FOUNDATION QUESTIONS EXERCISE, 1 For a particle in a non-uniform accelerated circular, (a) velocity is radial and acceleration is transverse, , (b)velocity is transverse and acceleration is radial only, acceleration has both radial and, , transverse components, , (d) velocity is, , transverse and acceleration has both radial, , and transverse components, 2 An athlete, , completes, , one, , round of, , radius 10m and time period 40, by him in 2 min 20 s is, (a) 70 m, , (b) 140 m, , magnitude of the centripetal, , acceleration of, , the stone while in circular motion?, , motion correct statement is, , (c) velocity is radial and, , What is the, , s., , a, , circular track of, , The distance covered, , (c) 110 m, , (b) 64 ms-, , (a) 163 ms2, (c)15.63 ms2, , (d) 125 ms2, , 9 A particle moves in a circle of radius 5 cm with constant, speed and time period 0.2 t s. The acceleration of the, (a) 25 m/s, , CBSE AIPMT 2011, (b) 36 m/s2, , (c) 5 m/s, , (d) 15 m/s, , particle is, , 10 In the given figure, a = 15 m/s represents the total, , acceleration of a particle moving in the clockwise, (d) 220 m, , 3 A car wheel is rotated to uniform angular acceleration, , direction in a circle of radius R = 2.5 m at a given instant, , of time. The speed of the particle is, , NEET 2016, , about its axis. Initially its angular velocity is zero. It, rotates through an angle 6, in the first 2s, in the next 2s, it, , rotates through an additional angle 0, the ratio of 2 is, , R, , 30, a, , (a) 1, (c) 3, , (b) 2, , (d) 5, , 4 Which of the following statements is false for a particle, moving in a circle with a constant angular speed., , (a) The velocity vector is tangent to the circle, (b) The acceleration vector is tangent to the circle., , (c) The acceleration vector point to the centre of the circle, , (d) The velocity and acceleration vectors are perpendicular, to each other., , 5 A particle moves along a circle of radius, , m with, , (a) 4.5 m/s, , (b) 5.0 m/s, , (c) 5.7 m/s, , 11 A uniform circular disc of radius 50 cm at rest is free to, , turn about an axis which is perpendicular to its plane and, passes through its centre. It is subjected to a torque, which produces a constant angular acceleration of, , 2.0 rad s . Its net acceleration a in msat the end of, NEET 2016, , 2.0 s is a approximately, , constant tangential acceleration. If the velocity of the, particle is 80 m/s at the end of the second revolution, after motion has begain, the tangential acceleration is, , (a) 160R m/s (b) 40 m/s2, , (c) 40m m/s, , (d) 640T m/s?, , 6 An electric fan has blades of length 30 cm measured, , from the axis of rotation. If the fan is rotating at 120, rev/min, the acceleration of a point on the tip of the, blade is, , (a) 1600 m/s (b) 47.4 m/s, , (c) 23.7 m/s, , (d) 50.55 m/s, , 7 An aircraft executes a horizontal loop of radius 1 km with, , a speed of 900 kmh. Ratio of centripetal acceleration to, acceleration due to gravity is, (a) 12.3, , (c) 6.4, , (b) 3.3, (d) None of these, , 8 A boy whirls a stone in a horizontal circle of radius 1.5 m, , and at height 2.0 m above level ground. The string, , breaks and the stone flies off tangentially and strikes the, ground after travelling a horizontal distance of 10 m., , (d) 6.2 m/s, , (a) 7:0, , (b) 6.0, , (c) 3.0, , (d) 8.0, , 12 A particle of mass 100 g tied to a string is rotated along, a circle of radius 0.5 m. The breaking tension of string is, 10 N. The maximum speed with which particle can be, rotated without breaking the string is, , (a) 10 ms-1, (c) 7.7 ms, , (b) 9.8 ms, (d) 7.07 ms, , 13 A proton of mass 1.66 x10, , kg goes round in a circular, , órbit of radius 0.10 m under a centripetal force of, , 4x10, , N, then the frequency of revolution of the proton, , is about, , (a) 008 x10 cycle/s, , (b) 4 x 10° cycle/s, , (c) 8x 10°cycle/s, , (d) 12 x 10° cycle/s, , 14 If the radius of curvature of the path of two particle of, same masses are in the ratio 1:2, then in order to have, , constant centripetal force, their velocity should be in the, ratio of, , (a)1:4, , (b)4: 1, , (c) 4:2, , (d) 1 2

Page 2 :
15 One end of the string of length /is connected to, , a, , particle of, , and the other end is connected to a small peg on a, smooth horizontal table. If the particle moves in circle with, speed v, the net force on the particle (directed towards center), NEET 2017, will be (7 represents the tension in the string), mass m, , (a) T, , (b)T+mV (c)7mv, , (d) Zero, , (a) 1 cmn, , on a, , rotating, , (b) 2 cm, , turn table, , (c) 4 cm, , (d) 8 cm, road turn, , 17 What will be the maximum speed of a car on a, of radius 30 m, if the coefficient of friction between, the, tyres and the road is 0.4?, , (Take. g= 9.8 m/s*), (a) 10.84 m/s, , (b) 9.84 m/s, , (c) 8.84 m/s, , (d) 6.84 m/s, , velocity with which a car driver must, traverse a flat curve of radius 150 m and coefficient of, friction 0.6 to avoid skidding?, , 18 The maximum, , (a) 60, , (b) 30, , (c) 15, , (d) 25, , (b) tan (064), (d) None of these, , (a)sin (064), (c)cos (064), 20 A, , car, , of, , mass, , radius 90, , just slips, if it is, centre. If angular, the, from, cm, placed at a distance of 8, at a, velocity of the turn table is doubled, it will just slip, distanceof, , 16 A coin placed, , 400 m in, 19 A cyclist goes round a circular path of length, from, vertical in, 20 s. The angle through which he bends, is, balance, the, order to maintain, , m, , 1000, , on a, , kg negotiates, , frictionless road. If the banking, , 45°, the speed of the, , (a) 20 ms, , banked curve of, , a, , car, , (b) 30 ms, , angle is, , CBSE AIPMT 2012, , is, , (c) 5 ms, , (d) 10 ms, , 21 Find the maximum velocity with which a train can be, moved on a circular track of radius 200m. The banking of, AFMC 2011, O.1), the track is 5.71° (Given, tan 5.71°, =, , (a), , 1.4 m/s, , (b) 14 m/s, , (c), , 140 m/s, , (d) 0.14 m/s, , 22 A cyclist riding the bicycle at a speed of 14/3 m/s takes, a turn a circular road of radius 20V3 m without skidding, What is his inclination to the vertical?, (c) 48°, (b) 90°, (a) 30, , (d) 60, , m forms an arc of radius 15 m, its, m, 2, is, higher than its inner edge. For what, edge, banked?, is, road, the, velocity, , 23 A road of width 20, outer, , (a)v10ms, , (b)14.7 ms, , (c)V98 ms, , (d), , None of these