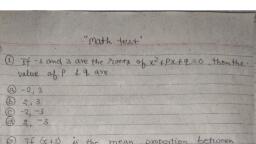Page 1 :
Complete Ters+ @, , 0 If x = 4 (mod 7), then positive values of x are, , (a) (4,11, 18, ...} (b) (11, 18, 25, ...} (c) (4,8, 12, ...) (a) (1,8, 15, ...}, , @ In what ratio must water be mixed with milk to gain 162% on selling the mixture at cost, price?, (a) 1:6 (b) 6:1 (c) 3:2 (d) 2:3, , Amerchant has 1000 kg of sugar. Part of which he sells at 8% profit and the rest at 18% profit., He gains 14% on the whole. The quantity sold at 18% profit is, (a) 400 kg (b) 600 kg (©) 560 kg (d) 640 kg, @ The speed of a boat in still water is 15 km/h and the rate of current is 3 km/h. The distance, travelled by boat downstream in 12 minutes is, (a) 1.2km (b) 1.8km (c) 24km (d) 3.6 km i, © A boat covers a certain distance downstream in 1 hour while it comes back in 1— hours. If, the speed of the stream be 3 km/h, what is the speed of boat in still water?, (a) 12km/h (6b) 13km/h (c) 14km/h (d) 15km/h, , © A and B invest in a business in the ratio 5 : 6. If 10% of the profit goes to charity and A get, % 4500 as his share in profit, the total profit is, , (a) %11000 (b) %12100 (c) %13200 (d) 79900, In a 300 m race, A beats B by 22.5 m or 6 seconds. B’s time over the race course is, (a) 80 see (b) 82 sec (c) 76 sec (d) 90 sec, ® Given that x, y and b are real numbers and x 2 y, b > 0, then, 23s estt r<% <2, © 55 Oo o Ee OF*;, O tex eR, |x| 2-7, then, (a) x € (-*,-7)U (7,0) (b) x € (-~,-7) U[7, »), (c) x € [-7,7] (d) rxEeR, , It |2v+3] <7,xe R, then, , (b) x € (-5, 2), (d) xe (-™, -5] U [2, wm), , (a) ve (-5, 2], (xe *, -5) U (2, ©), ® The solution set of 6 -3(2¥ = 4) < 12.0 a”, (@) (0.1) (b) [1.0, , @ 1/3 1, at = | (x ~6), x € R, then, Walger 4a) ese ), , (a) xe (-«, 120] (b) x € 11204), Given that x, y and b are real numbers and x 2 y, b > 0, then, , i) OD) (a) (0,1), , (c) ve (-®, 120) (d) x € (120, »), , sz zee Ser. Zed., @) 525 () >> (c) Ps M ><, Ifx eR, |x| <-3, then, , (a) 3<x<-3 (b) -3<x<3 (c) -3<xs3 (a) xeo

Page 2 :
The sum of two natural numbers is 25 and their difference is 7. The numbers are, , (a) 17 and 8 (b) 16 and 9 (c) 18 and 7 (d@) 15 and 10, The sum of the digits of a two digit number is 12. If the number is decreased by 18, its digits, get reversed. The number is, , (a) 48 (b) 84 (c) 57 (d) 75, The solution of the svstem of equations : + 5y=7 and is 4u =5is, , 1, , (a) x= —,y=-1 (b) r=-1y=1 (c) x=3,y=-1 (d) x=-3,y=1, , 3, , Father's age is six times his son’s age. Four years hence, the age of the father will be four, times his son's age. The present age in years of the son and the father are respectively, , , , (a) 4and 24 (hb) Sand 30 (ce) 6 and 36 (dl) Sand 24, @ WA : : J and! | ; , . then A? - 6A is equal to, -|, (a) 31 (b) -SI () 51 (d) none of these, 9) The number of all possible matrices of order 3 x 3 with each entry 0 or Lis, (a) 18 (b) 27 (e) 81 (d) 512, If Ais a square matrix such that A? = 1, then (A + D8 + (A= 13 = 7A is equal to, WA (b) A-1 (ce) Atl (d) 3A, QD risa square matrix such that A? = A, then (I~ A)" + A is equal to, (a) 1 (b) 0 (c) I-A (dy +A, 12, 3) liA= * | and A? — vA = 1,, then the value ot vis, qa) 4 (b) 2 («) -2 qi) -4, hi ey then A? is equal to, A» la, }oc> where +z A> is equa, It A® la,}yc9 where ay “{o it i<j ie “, wl (b) A «) O (d) none of these, It for matriv A, A* = Lthen A !&> (a) A (by) Ae (e) AS (d) none of these, 2, @® If A7-A+1=O, then A-! is equal to, (a) A+] (b) A-1 (, : c) A+2I (a) I-A, ‘ a square matrix of order 3 and |A, ye (b) 2 | = 2, then the value of |-AA'| is, 3 # Sin dea mist (d) -4, é : uare matrix ler3a ®, ~~ ie nd |A| =5, then the value of |2A°| is, @- (c) -40 (d) 40

Page 3 :
() yan? non-singular square matrix of order 3 such, , , , ® 3 that A2 = 3A, then the value of | A] is, , “= : () 9 (27, 6 The interval on which the function f(x) = 2x3 + 9x2 + 12x-1 is decreasing is, , anes © (-«,-2 (© (-2,-1] @{-1.11, ® The function f(x) = x? e* strictly increases on nee, , (a) (0,2) (b) -s @ Camune dems, , The minimum value of bee is, , (a) ¢ (b) i () 2 (d) 2e, @) The maximum slope of the curve y = —x3 + 3x2 + 9x - 27 is, , (a) 0 (b) 12 (c) 16 (d) 32, , 6) If the selling price of a commodity is fixed at 7 45 and the cost function is C(x) = 30x + 240,, , then the breakeven point is, ") ¥=30 (b) x= 12 (©) x=15 () 5-16, If the demand function is p(x) = 20 - = then the marginal revenue wnen x = O1s, (a) 25 (b) 710 () %15 (d) 7150, , ® The least value of the function f (x) = ax + ate >0,a>0,b>0) is, , (a) Jab (b) 2Vab (c) ab (d) 2ab, ® A dice is thrown twice, the probability of occurring of 5 atleast once is, nl 4%, x (d) none of these, (a) ry (b) IR (c) 36, (GB Fora binomial variate X, ifm = 3 and P(X = 1) = 12 P(X = 3), then the value of p is, 2 1 2, (a) 2 (b) 3 () 3 (d) :, © If X is a Poisson variable such that P(X = k) = P(X = k + 1), then variance of X is, (a) k-1 (b) k (c) k+1 (d) k+2, , (54) If X has a Poisson distribution such that P(X = 1) = P(X = 2) and ? = 0.1353, then P(X = 4), is, (a) 0.0213 (b) 0.9787 (c) 0.0902 ~ (d) 0.9098, Ina binomial distribution, the probability of getting a success is + and the standard deviation, is 3. Then its mean is ., (a) 6 (b) 8 (¢) 12 (a) 48