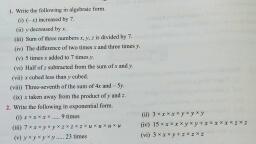Question 1 :
The smallest set $A$ such that $A\cup \left\{ 1,2 \right\} =\left\{ 1,2,3,5,9 \right\} $ is 
Question 3 :
If $M = \left\{ {x:x \geqslant 7\,\,{\text{and}}\,x \in N} \right\}$ for universal set of natural numbers, then $M'$ is
Question 4 :
Which of the following represents singleton set.<br/>$(i)A=\{x:x$ is an even prime number$\}$ <br/>$(ii)y:y$ is a whole number which is not a natural number.<br/>$(iii)x:x\in I, 1<x\le3$
Question 5 :
Find out the truth sets of the following open sentences replacement sets are given against them.<br/>$x+\dfrac{1}{x}=2; \{0, 1, 2, 3\}$
Question 6 :
Find out the number of elements in the following set:$A= \{ x| x \epsilon N, 2 < x <4 \}$.
Question 11 :
Out of 800 boys in a school, 224 played cricket, 240 played hockey and 336 played basketball. Of the total, 64 played both basketball and hockey ; 80 played cricket and basketball and 40 played cricket and hockey 24 player all the three games. The number of boys who did not play any game is
Question 12 :
If A={$x\in N$ : xis a multiple of 3} and<br>B={$x\in N$ : is a multiple of 6}, then A-B is equal to
Question 13 :
Let $ S=\left\{1,2,3,.....40\right\} $ and let $A$ be a subset of $S$ such that no two elements in $A$ have their sum divisible by $5$ What is the maximum number of elements possible in $A$?<br>
Question 14 :
Let $A=\{x:x\in R\  \&\ x^2+1=0\}$ then $A$ is a null set.
Question 15 :
The sets $\displaystyle S_{x}$ are defined to be $(x, x + 1, x + 2, x + 3, x + 4)$ where $x=1, 2, 3,.....80$. How many of these sets contain $6$ or its multiple? 
Question 16 :
If $A$ and $B$ are any two non-empty sets, then prove that $(A\cap B)'=$ 
Question 17 :
Identify the type of set$B = \{x : x\ is\  a\  composite\  number\  less\  than\ 5 \}$.
Question 18 :
Let $\displaystyle A= \left \{ 7,8,9,a,b,c \right \} $ and $\displaystyle B= \left \{ 1,2,3,4 \right \} $ then number of universal relation from the set $A$ to set $B$ and set $B$ to set $A$ are<br/>
Question 19 :
Find sets $A,B$ and $C$ such that $A\cap B,B\cap C$ and $C\cap A$ are non-empty sets and $A\cap B\cap C=\phi.$
Question 20 :
$A = \{x | x \in I, x^2$ is not positive$\}$<br/>Then $A$ is a <br/>