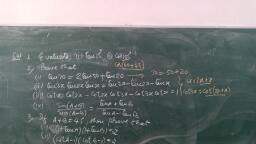Question 1 :
Given $P(A \cup B)=0.6, P(A\cap B)=0.2$, the probability of exactly one of the event occurs is

Question 2 :
Let $A$ is a finite set such that $n(A)=6$ then  $n[P(A)]$ is 

Question 3 :
Classify the following set as 'singleton' or 'empty': $A = \{ x | x$ is a negative natural number$\}$

Question 6 :
The value of c for which the set $\{(x, y)|x^2+y^2+2x\leq 1\}\cap \{(x, y)|x-y+c\geq 0\}$ contains only one point in common is?

Question 7 :
If n is a member of both set A$=\left\{\displaystyle\frac{4}{7}, 1, \frac{5}{2}, 4, \frac{1}{2}, 7\right\}$ and set B$=\left\{\displaystyle\frac{4}{7}, \frac{7}{4}, 4, 7\right\}$, which of the following must be true?<br>I. n is an integer.<br>II. $4n$ is an integer.<br>III. $n=4$

Question 9 :
Which of the following regarding null sets are correct.<br>$(i)$ Empty set is considered as subset of all sets.<br>$(ii)$ Union of an empty set $\phi$ with a set $X$ is an empty set.<br>$(iii)$ Intersection of an empty set with a set $X$ is X.

Question 11 :
If $R$ is a relation on the set $A=\left\{ 1,2,3,4,5,6,7,8,9 \right\} $ given by $xRy\Leftrightarrow y=3x$, then $R=$

Question 12 :
Let the number of elements of the sets $A$ and $B$ be $p$ and $q$ respectively. Then, the number of relations from the set $A$ to the set $B$ is

Question 13 :
If $A=\left \{x:x^2-3x+2=0\right \}$ and $B=\left \{x:x^2+4x-5=0\right \}$ then the value of A-B is

Question 14 :
Let R be the relation in the set N given by = {(a, b): a = b - 2, b &gt; 6}. Choose the correct answer

Question 15 :
The relation $R$ defined on the set $A=\left\{ 1,2,3,4,5 \right\} $ by $R=\left\{ \left( a,b \right) :\left| { a }^{ 2 }-{ b }^{ 2 } \right| &lt;16 \right\} $, is not given by

Question 16 :
The relation R define on the set of natural numbers as {(a, b) : a differs from b by 3} is given.

Question 17 :
Let $A$ and $B$ be two sets containing four and two elements respectively.Then the number of subset of the set $A \times B$, each having at least three elements is <br>

Question 18 :
If $\displaystyle :n(A)= m, $ then number of relations in $A$ are<br/>

Question 19 :
Let $A = \left\{ {a,\,b,\,c} \right\}$ and $B = \left\{ {4,\,5} \right\}$. Consider a relation defined from set A to set B, then R is equal to

Question 20 :
The domain of the relation R = $\displaystyle \left \{ \left ( x,y \right ):x,y\epsilon N \ and\ x+y\leq 3 \right \}$ is____

Question 21 :
Two complex numbers are represented by ordered pairs $z_1: (a,b)\ \&amp;\ z_2: (c,d)$, when these two complex numbers are equal?

Question 22 :
$i^n + i^{n + 1} + i^{n + 2}+ i^{n + 3} (n &#160;&#160;\in &#160;&#160;N) $ is equal to

Question 23 :
Find all complex numbers $z$ which satisfy the following equation<br>$z=-\bar { z }$<br>

Question 25 :
The real part of $(1 - \cos\theta + 2i \sin\theta)^{-1}$ is:

Question 28 :
Find the value of $\dfrac{sin (-660^o) tan (1050^o) sec (-420^o)}{cos (225^o ) cosec (315^o) cos(510^o)}$

Question 30 :
If $\theta$ is in the first quadrant and cos $\theta=\frac{3}{5}$, then the value of $\dfrac{5 tan \theta -4cosec \theta}{5 sec\theta-4cot \theta}$ is<br/><br/>

Question 31 :
The angle subtended at the centre of circle of radius $3$ metres by an arc of length $1$ metre is equal to

Question 34 :
$\tan\theta=-2, &#160;\theta \epsilon &#160;(0, \pi)$ then which of the following is correct

Question 35 :
If $a = \sin {170^ \circ } + \cos {170^ \circ }$, then

Question 36 :
The measure of an angle in degrees, grades and radians be D, G and C respectively, then relation between them $\displaystyle \frac{D}{90}=\frac{G}{100}=\frac{2C}{\pi }$ but $\displaystyle 1^{\circ}=\left ( \frac{180}{\pi } \right )^{\circ}\:\simeq 57^{\circ},17',44.{8}''$ and sum of interior angles of a $n$-sided regular polygon is $\displaystyle \left ( 2n-4 \right )\dfrac {\pi }2$. On the basis of above information, answer the following questions :Which of the following are correct<br/>

Question 37 :
If&#160;$\displaystyle \alpha \, and\, \beta $ are angles in the first quadrant&#160;$\displaystyle \tan \alpha =\frac{1}{7},\sin \beta =\frac{1}{\sqrt{10}}$ then using the formula&#160;$\displaystyle \sin (A+B)=\sin A\cos B+\cos A\sin B$ one can find the value of&#160;$\displaystyle (\alpha +2\beta )$ to be&#160;

Question 38 :
If $\displaystyle&#160;\frac { 3\pi &#160;}{ 4 } &lt;\alpha &lt;\pi $, then $\displaystyle&#160;\sqrt { 2\cot { \alpha &#160;} +\frac { 1 }{ \sin ^{ 2 }{ \alpha &#160;} &#160;} &#160;} $ is equal to

Question 39 :
The degree measure of 1 radian (taking $\pi =\dfrac { 22 }{ 7 }$ ) is