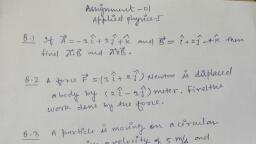Question 1 :
A particle is moving along a circular path of radius $5\ m$ with a uniform speed $5\ ms^{-1}$. What will be the average acceleration when the particle completes half revolution?
Question 2 :
A particle is moving along a circular path with a constant speed $30\,m/s$. What is change in velocity of particle, when it decreases an angle of ${90^ \circ }$ at the center of the circle ?
Question 3 :
A car starts from rest and accelerates uniformly over a time of $5.21$ seconds for a distance of $110$ m. Determine the acceleration of the car.<br/>
Question 4 :
A train is moving with a velocity of $90\  kmph$. When brakes are applied, the retardation produced is $0.5 m{s}^{-2}$. Find the time taken by the train to come to rest.
Question 5 :
Two cars A and B move such that car A moving with a uniform velocity of $15\ ms^{-1}$ overtakes car B starting from rest with an acceleration of $3\ ms^{-2}$. After how much time do they meet again?<br/>
Question 6 :
A block of mass 2 kg falls from the wall at height of 2.3 m. Calculate the velocity just before it hits the ground. ($g=-9.8 \frac{m}{s^2}$)<br/>
Question 7 :
Identical constant forces push two identical cars A and B continuously from a starting line to a finish line. The cars move on a frictionless horizontal surface. If car A is initially at rest and car-B is initially moving right with speed $Vo.$ Choose the correct statement
Question 8 :
A mass m rotates in a vertical circle of radius, R and has a circular speed $v_{c}$ at the top .- If the radius of the circle is increased by a factor of 4,, circular speed at the top will be
Question 9 :
Assertion: A negative acceleration of a body can be associated with a speeding up of the body.
Reason: Increase in speed of a moving body is independent of its direction of motion
Question 10 :
A boy sitting on the top most berth in the compartment of a train which is just going to stop on the railway station, drops an apple aiming at the open hand of his brother situated vertically below his hands at a distance of about 2 m. The apple will fall
Question 11 :
Two bodies, one held 30 cm directly above the other, are released simultaneously and allowed to fall freely under gravity. After 2 s their relative separation will be :<br/>
Question 12 :
A body travelling with uniform acceleration crosses two points $A$ and $B$ with velocities $20\ ms^{-1}$ and $30\ ms^{-1}$ respectively. The speed of the body at mid-point of $A$ and $B$ is:
Question 13 :
The velocity of a body which starts from rest with an acceleration $2\ ms^{-2}$ and covering a distance of $10\ m$ in $ms^{-1}$ is:<br/>
Question 14 :
A freely falling body takes $t$ second to travel first $(\dfrac{1}{x})^{th}$distance. Then, time of descent is
Question 15 :
A body starts with an initial velocity of $10 m s^{-1}$ and acceleration $5 m s^{-2}$. Find the distance covered by it in $5\  s$.
Question 16 :
If you were to throw a ball vertically upward with an initial velocity of $50 \; ms^{-1}$, approximately how long would it take for the ball to return to your hand? Assume air resistance is negligible. (Given $g=10\; ms^{-2}$)
Question 17 :
Assertion: A body with constant acceleration always moves along a straight line.
Reason: A body with constant magnitude of acceleration may not speed up.
Question 19 :
What should be the projection velocity for a body to reach the same height on the Moon as compared to that on the Earth?<br/>
Question 20 :
A stone projected vertically upwards reaches to the level of window 10 m from the ground. Find the magnitude of velocity of the stone at the time of its projection.
Question 21 :
A stone of mass $200\ g$ thrown up with a certainvelocity reaches a maximum height of $30 $ m.Another body of double the mass is thrown upwith half the velocity of the first. Maximum height reached by it is
Question 22 :
Gradient of line of velocity time graph is tells us the
Question 23 :
If a car at rest accelerates uniformly and attains a speed of 72 km/hr in 10 s, then it covers a distance of:
Question 24 :
A police party is chasing a dacoit in a jeep which is moving at a constant speed v. The dacoit is on a motorcycle. When he is at a distance $x$ from the jeep, he accelerates from rest at a constant rate? Which of the following relations is true if the police is able to catch the dacoit?
Question 25 :
A particle is moving in a circle in a radius $r$ with a constant speed $v$ . The change in velocity after the particle has traveled a distance equal to $(\dfrac{1}{8})^{th}$of the circumference of the circle is:
Question 26 :
A stone is thrown in vertically upward direction with a velocity of $5\ ms^{-1}$. If the acceleration of the stone during its motion is $10\ ms^{-2}$ in the downward direction, what will be the height attained by the stone and how much time will it take to reach there?<br/>
Question 27 :
When a body is projected vertically up from the ground its velocity is reduced to $\frac{1}{4}$th of its velocity at ground at height $h$. Then the maximum height reached by the body is<br/>
Question 28 :
The position is a particle along a straight line is denoted by the equation $x = 6 + 12 t - t^3$. (Here $x$ is in meter and $t$ is in second). The magnitude of acceleration of the particle when it is at rest is:-
Question 29 :
A car starts from rest and accelerates on a straight horizontal track at $5 {m}/{{s}^{2}}$. Find out the distance travel by the car in $8$ seconds?
Question 30 :
If a body is thrown up with an initial velocity u and covers a maximum height of h, then h is equal to<br>
Question 31 :
A body moving with uniform acceleration in a straight line is at points A, B, C, D after successive equal intervals of time. The distance AD is equal to:
Question 32 :
A body with an initial velocity of $18 kmph$ accelerates uniformly at $9 cm{s}^{-2}$ over a distance of $200 m$. Find its final velocity in $m{s}^{-1}$.
Question 33 :
If a ball is dropped from rest, it will fall 20m during the first two seconds. How far will it fall during the third and fourth seconds?
Question 34 :
Assertion: Two similar trains are moving along the equatorial line with the same speed but in opposite direction. They will exert equal pressure on the rails.
Reason: In uniform circular motion the magnitude of acceleration remains constant but the direction continuously changes.
Question 35 :
Assertion: Acceleration and displacement are in the opposite direction during retardation.
Reason: Acceleration is given as the change in velocity per unit time.
Question 36 :
When a bus driver travelling at a speed of 20m/sapplied brakes and brings the bus to rest in 10seconds, then retardation will be
Question 37 :
A particle moves along x-axis in such a way its coordinate (x) varies with time (t) according to the expression $x=2-5t+6t^2$. its intial velocity is<br>
Question 38 :
A stone thrown vertically upwards with a speed of $5{ m }/{ s }$ attains a height ${ H }_{ 1 }$. Another stone thrown upwards from the same point with a speed of $10{ m }/{ s }$ attains a height ${ H }_{ 2 }$. The correct relation between ${ H }_{ 1 }$ and ${ H }_{ 2 }$ is<br>
Question 39 :
The area under the velocity-time graph between any two instants  $t = t_{1}$ and $t =t_{2}$ gives the displacement in time $\delta t=t_{2}-t_1$ :
Question 40 :
A car was moving at $1m{s}^{-1}$ when brakes were applied. The brakes offered a retardation of $0.5m{s}^{-2}$. If the brakes are applied for $2 s$, after $2 s$
Question 41 :
A stone is dropped from a balloon at an altitude of $280$ m. If the balloon ascends with a velocity of $5\ ms^{-1}$ and descends with a velocity of $5\ ms^{-1}$, times taken by the stone to reach the ground in the two cases respectively are ($g=10\ ms^{-2}$):
Question 42 :
A body, projected vertically up with a velocity of $20\;ms^{-1}$, reaches a height of $20\;m$. If it is projected with a velocity of $40\;ms^{-1}$, then the maximum height reached by the body is:
Question 43 :
When the speed of a car is $v$, the minimum distance over which it can be stopped is $s$. If the speed becomes $nv$, what will be the minimum distance over which it can be stopped during the same time?<br>
Question 45 :
The distance covered by a body moving alone-X-axis with initial velocity 'u' and uniform acceleration 'a' is givenby $\displaystyle x=ut+\frac{1}{2}at^{2}$. This result is a consequence of
Question 46 :
A particle travels $10$m in first $5$ seconds $10$ cm in next $3$ seconds. Assuming constant acceleration what is the distance travelled in next $2$ second ?
Question 47 :
Is the policeman right in arresting the driver to break speed limit?<br>
Question 49 :
A plane has a takeoff speed of $88.3 m/s$ and requires $1365 m$ to reach that speed. Determine the acceleration of the plane.
Question 50 :
A ball is dropped downwards, after $1$ sec another ball is dropped downwards from the same point. What is the distance between them after $3$ sec? (Take $g=10ms^{-2}$)