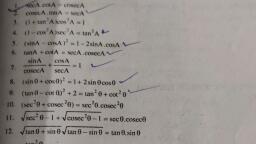Question 1 :
If $\displaystyle \frac { x\text{ cosec }^{ 2 }{ 30 }^{ o }{ \sec }^{ 2 }{ 45 }^{ o } }{ 8{ \cos }^{ 2 }{ 45 }^{ o }{ \sin }^{ 2 }{ 90 }^{ o } } ={ \tan }^{ 2 }{ 60 }^{ o }-{ \tan }^{ 2 }{ 45 }^{ o }$, then $x$ is :

Question 4 :
The value of $\cos 1^{\circ}. \cos 2^{\circ}. \cos 3^{\circ} ...\cos 179^{\circ}$ is equal to:

Question 5 :
The value of$\displaystyle \frac { \cos { \left( { 90 }^{ o }-A \right) } }{ 1+\sin { \left( { 90 }^{ o }-A \right) } } +\frac { 1+\sin { \left( { 90 }^{ o }-A \right) } }{ \cos { \left( { 90 }^{ o }-A \right) } }$ is equal to :

Question 6 :
If $\cos\theta = \dfrac{14}{4}$ and $\sin\theta$ $=$ $\dfrac{8}{3}$, what is the value of $\cot\theta$?<br/>

Question 9 :
If A and B are acute angles such that $sin &#160;A=\sin^{2}B, &#160;2 \cos^{2}A=3&#160; \cos^{2}B;$ then

Question 10 :
$\sin 84^{\circ} + \sec 84^{\circ}$ expressed in terms of angles between $0^{\circ}$ and $45^{\circ}$ becomes

Question 11 :
The value of $\displaystyle \csc (65^0+\theta )-\sec (25^0-\theta )-\tan (55^0-\theta )+\cot (35^0+\theta )$ is<br/>

Question 12 :
If $\displaystyle x=r\sin \theta \cdot \cos \phi,$ &#160;$y=r\sin \theta \cdot \sin \phi$ and $\displaystyle z= r\cos \theta$, then the value of $\displaystyle x^{2}+y^{2}+z^{2}$ is independent of&#160;

Question 14 :
Find the value of ${k}$ for which $(\cos x+\sin x)^{2}+k\sin x\cos x-1=0$ is an identity.<br/>

Question 15 :
The value of $\sec$ $(90^0 - \theta) \sin \theta$ is <br/><br/><br/>

Question 16 :
If $\sec \theta - \cos \theta = 1$, then $\tan^{2} \theta=$<br/>

Question 17 :
The value of ${ e }^{ \log _{ 10 }{ \tan { 1+ } } \log _{ 10 }{ \tan { 2+\log _{ 10 }{ \tan { 3+...+\log _{ 10 }{ \tan { 89 } } } } } } }$ is

Question 18 :
$\displaystyle &#160;cosec \ \theta =\frac{x^{2}-y^{2}}{x^{2}+y^{2}}$, where $x\in R, y \in R$ , gives real $\theta$ if and only if :

Question 19 :
The value of the expression$\displaystyle \frac {tan^2 20^0 - sin^2 20^0}{tan^2 20^0 . sin^2 20^0}$ is

Question 20 :
The value of&#160;$\displaystyle \sec { { 41 }^{ o } } \sin { { 49 }^{ o }+ } \cos { { 49 }^{ o } } \text{cosec }{ 41 }^{ o }$ is :

Question 22 :
<p>Suppose ABC is a triangle with 3 acute angles A, B, and C. The point whose coordinates are (cosB-sinA, sinB-cosA)can be in the-</p>

Question 24 :
If &#160;$\displaystyle \theta \in \left ( 0,\frac{\pi }{2} \right )$, then the value of $\displaystyle \cos \left ( \theta -\frac{\pi }{4} \right )$&#160;lies in the interval

Question 25 :
If $3\cot \theta = 4$ then $\dfrac {5 \sin&#160;\theta + 3 \cos&#160;\theta}{5 \sin&#160;\theta - 3 \cos \theta} = $_____

Question 27 :
Find the value of $\dfrac {\cos 75^{\circ} . \sin 12^{\circ}. \cos 18^{\circ}}{\sin 15^{\circ}. \cos 78^{\circ} . \sin 72^{\circ}}$

Question 28 :
Solve: $\sec 70^{\circ} \sin 20^{\circ} + \cos 20^{\circ} \text{cosec } 70^{\circ} $

Question 29 :
Write True or False and justify your answerin each of the following :<br>$ (tan \theta + 2)(2 \, tan \theta + 1) = 5 \, tan \theta + sec^2 \theta $<br>

Question 31 :
The value of $\cos { { 10 }^{ 0 } } -\sin { { 10 }^{ 0 } } $ is?<br/>

Question 32 :
Evaluate: $\cfrac { \sin { \theta &#160;} \cos { \theta &#160;} \sin { \left( { 90 }^{ o }-\theta &#160;\right) &#160;} &#160;}{ \cos { \left( { 90 }^{ o }-\theta &#160;\right) &#160;} &#160;} +\cfrac { \cos { \theta &#160;} \sin { \theta &#160;} \cos { \left( { 90 }^{ o }-\theta &#160;\right) &#160;} &#160;}{ \sin { \left( { 90 }^{ o }-\theta &#160;\right) &#160;} &#160;} +\cfrac { \sin ^{ 2 }{ { 27 }^{ o } } +\sin ^{ 2 }{ { 63 }^{ o } } &#160;}{ \cos ^{ 2 }{ { 40 }^{ o } } +\cos ^{ 2 }{ { 50 }^{ o } } &#160;} $

Question 33 :
Find the value of $\tan 10^{\circ} \tan 15^{\circ} \tan 75^{\circ} \tan 80^{\circ} $

Question 35 :
The value of&#160;$\displaystyle \sin^{3} \alpha \left ( 1+\cot \alpha &#160;\right )+\cos ^{3}\alpha \left ( 1+\tan \alpha &#160;\right )$ is equal to

Question 37 :
If $p=\sec\alpha-\tan\alpha , q = \text{cosec }\alpha+\cot\alpha$. Find $q$ in terms of $ p$.<br/>

Question 39 :
If $7 \theta $ and $2 \theta$ are measure of acute angles such that&#160; sin $7\theta$=cos $2 \theta$, then $2sin 3\theta-\sqrt3$ tan $3\theta$ is ________.

Question 40 :
$\tan 1^{\circ} \tan 2^{\circ} \tan 3^{\circ} ... \tan 89^{\circ} = $

Question 41 :
$\sin 81^{\circ} + \tan 81^{\circ}$, when expressed in terms of angles between $0^{\circ}$ and $45^{\circ}$, becomes

Question 42 :
$\cos 75^{\circ} + \cot 75^{\circ}$, when expressed in terms of angles between $0^{\circ}$ and $30^{\circ}$, becomes

Question 43 :
The value of$ \displaystyle \tan 1^{\circ}\tan 2^{\circ}\tan 3^{\circ}.....\tan 89^{\circ} $ is

Question 44 :
If $\sin A + \sin^{2}A + \sin^{3}A&#160;= 1$, then find the value of $\cos^{6}A-4\cos^{4}A + 8\cos^{2}A$ is:

Question 45 :
Match the following columns with the values obtained for the solution.<br/><table class="wysiwyg-table"><tbody><tr><td>$I.$<br/>$x\cos \theta+ y\sin \theta=a$,<br/>$x\sin \theta- y\cos \theta=b$<br/></td><td><br/>$a)$ $(x^{2}-y^{2})^{2}=16xy$ <br/><br/></td></tr><tr><td>$II.$<br/>$x= \sec \theta+\tan\theta$,<br/>$y=\sec\theta-\tan\theta$<br/></td><td>$b)$ $xy = 1$<br/></td></tr><tr><td>$III.$<br/>$x\sec \theta+ y\tan \theta=a$,<br/>$x\tan \theta+ y\sec \theta=b$<br/></td><td><br/>&#160;$c)$ $x^{2}-y^{2}=a^{2}-b^{2}$<br/><br/></td></tr><tr><td><br/>$IV.$&#160;<br/>$x=\cot\theta+\cos\theta$,<br/>$y=\cot\theta-\cos\theta$<br/></td><td><br/>&#160;$d)$ $x^{2}+y^{2}=a^{2}+b^{2}$<br/><br/></td></tr></tbody></table><br/>

Question 46 :
If $\sin \theta + \cos \theta = \sqrt {2}$, find the value of $\sin \theta \times \cos \theta$.

Question 47 :
If $\sin \theta, \cos \theta, \tan \theta$ are in $G.P$, then $\cos^{9}\theta+\cos^{6}\theta+3\cos^{5}\theta-1$ is equal to:<br/>