Question 1 :
Factorize ( 24 x<sup>2 </sup>+ 68 x y + 40 y<sup>2</sup> )
Question 2 :
A stream flows from A to B, a distance of 13.00 km. A man who can row in still water at 9.00 kmph, can row up and down in 3.60 hrs . What is the speed of the stream?
Question 3 :
The principal diagonal elements of the given matrix<br>{tex}\begin{bmatrix}-6 &2 \\-8 & 4\end{bmatrix} {/tex}are<br>
Question 4 :
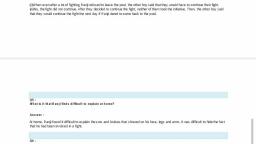
Find the number which is less than its square by 240
Question 5 :
Arun possesses 600 shares of ₹25 of a company. If the company announces a dividend of 8%, then Arun’s annual income is<br/>
Question 6 :
If the price of a commodity inclusive of sales tax is ₹11220.00 and the marked price is ₹11000.00, the rate of sales tax =
Question 7 :
If no of shares bought = 30 , face value = ₹20.00 , premium percent = 125.00%, rate of return = 3.11%, annual income on each share =
Question 8 :
A man invested ₹3150.00 in 5.00% ₹70.00 shares quoted at ₹90.00. When the market value of these shares rose to ₹130.00, he sold some shares, just enough to raise₹2210.00, find the dividend due to him on the remaining shares.
Question 9 :
If the price of a commodity inclusive of sales tax is ₹11897.60, the rate of sales tax is 4.00% and the rate of discount is 12.00%, the selling price =
Question 10 :
If the price of a commodity inclusive of sales tax is ₹6561.10, the marked price is ₹7000.00 and the rate of discount is 9.00%, the discount =
Question 11 :
Divide ₹195500.00 into two parts such that if one part is invested in 2.00%, ₹100.00 shares at ₹10.00 discount and the other in 4.00%, ₹100.00 shares at ₹50.00 discount , the annual incomes are equal.
Question 12 :
In the given figure, $CA$ and $C$. $B$ are tangent segments to the circle with centre $O$. Given {tex} \angle \mathrm{BCD}=22^{\circ} {/tex}, find {tex} \angle \mathrm{ABO} {/tex}<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e5bdba5935f6cc6ee57"><br>(i) Prove that {tex} \Delta \mathrm{ADF} \sim \Delta \mathrm{CEF} {/tex}.
Question 13 :
In the given figure, $ER \& FR$ are tangents to the circle with centre $O$. Given {tex} \angle \mathrm{EOF}=131^{\circ}, {/tex} find {tex} \angle \mathrm{ERF} {/tex}<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e6b2282923f071fae56"><br>
Question 14 :
If the two radii $OP$ and {tex} \mathrm{OQ} {/tex} of a circle are at right angles to each other, then the sector {tex} \mathrm{OPQ} {/tex} is called a<br>(iii) Find the ratio of the area of {tex} \Delta \mathrm{ADB} {/tex} is to area of {tex} \Delta {/tex}{tex}\mathrm{CDA}{/tex}.<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e4c2282923f071fae2e">
Question 15 :
In the given figure, two circles intersect at points {tex} D \& E{/tex} . A tangent is drawn at point $F$. From the same point, two lines are drawn passing through points {tex} \mathrm{D} \& \mathrm{E} {/tex}. They meet the other end of the second circle at {tex} \mathrm{C} \& \mathrm{B} {/tex}. Given {tex} \angle \mathrm{F}= {/tex} {tex} 82^{\circ}, {/tex} find {tex} \angle C D E {/tex}<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e68dba5935f6cc6ee69"><br>(ii) Find BC and CD.
Question 16 :
In the given figure, {tex} \mathrm{O} {/tex} is the centre of the circle and {tex} \mathrm{FH} {/tex} is the tangent at {tex} \mathrm{G} {/tex}. If {tex} \angle \mathrm{GHI}=45^{\circ}, \angle \mathrm{HGI}=34^{\circ}, {/tex} find {tex} \angle \mathrm{KGF} {/tex}<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e462282923f071fae22"><br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e46dba5935f6cc6ee3b">
Question 17 :
{tex} \mathrm{O} {/tex} is the centre of the circle. {tex} \mathrm{CD} {/tex} and {tex} \mathrm{ED} {/tex} are tangents to the circle. If {tex} \angle \mathrm{EFC}=30.5^{\circ}, {/tex} find {tex} \angle \mathrm{CDE} {/tex}<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e602282923f071fae43"><br>
Question 18 :
In the given figure, {tex} \mathrm{O} {/tex} is the centre of the circle and {tex} \mathrm{LM} {/tex} is the tangent at {tex} \mathrm{H} {/tex}. If {tex} \angle \mathrm{HKJ}=53^{\circ}, {/tex} find {tex} \angle \mathrm{MHJ} {/tex}<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e3d2282923f071fae0e"><br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e3ddba5935f6cc6ee2a">
Question 19 :
In the given figure, two circles intersect at points {tex} \mathrm{F} \& \mathrm{G} {/tex}. A tangent is drawn at point {tex} \mathrm{H} {/tex}. From the same point, two lines are drawn passing through points {tex} \mathrm{F} \& \mathrm{G} . {/tex} They meet the other end of the second circle at {tex} \mathrm{E} \& \mathrm{D} . {/tex} Given {tex} \angle \mathrm{H}= {/tex} {tex} 77^{\circ}, {/tex} find {tex} \angle \mathrm{EDG} {/tex}<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e65dba5935f6cc6ee65"><br>
Question 20 :
Two circles are of radii {tex} 3 \mathrm{~cm} {/tex} and {tex} 6 \mathrm{~cm} {/tex}. If the distance between their centres is {tex} 14 \mathrm{~cm} {/tex}, what is the length of their direct common tangent?<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e582282923f071fae38"><br>
Question 21 :
If two circles of radii {tex} 12 \mathrm{~cm} {/tex} and {tex} 5 \mathrm{~cm} {/tex} touch externally, the distance between their centres is
Question 22 :
In the given figure, {tex} \mathrm{O} {/tex} is the centre of the circle and {tex} \mathrm{FG} {/tex} is the tangent at {tex} \mathrm{B} {/tex}. If {tex} \angle \mathrm{BED}=42^{\circ}, {/tex} find {tex} \angle \mathrm{BCD} {/tex}<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e3c2282923f071fae0c"><br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e3cdba5935f6cc6ee28">
Question 23 :
Which of the following statements are true?<br>If two tangents to a circle intersect, their points of contact with the circle together with their point of a) intersection form an isosceles triangle b) If two tangents are parallel, the distance between them is equal to the diameter of the circle c) A line parallel to a tangent is a secant If two tangents are perpendicular, they form a right angled triangle with their points of contact with the circle d) and their point of intersection e) Two different tangents can meet at a point on the circle<br>
Question 24 :
In the given figure, FGHI is a cyclic quadrilateral such that HF bisects {tex} \angle \mathrm{IFG} {/tex} and {tex} \mathrm{JK} {/tex} is the tangent at {tex} \mathrm{H} . {/tex} If {tex} \angle \mathrm{HFG} {/tex} {tex} =58^{\circ}, {/tex} find {tex} \angle \mathrm{JHG} {/tex}<br /><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e59dba5935f6cc6ee53">
Question 25 :
The distance between the centres of two circles is {tex} d {/tex}. If the radii are {tex} r_{1} {/tex} and {tex} r_{2}, {/tex} the length of their direct common tangent is<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e31dba5935f6cc6ee16"><br>
Question 27 :
Which of the following statements are true?<br>a) If two circles touch each other externally, there is only one common tangent b) There exists four common tangents for any two non-intersecting circles c) If two circles intersect, then two common tangents can be drawn d) If two circles touch each other internally, there is only one common tangent<br>
Question 28 :
Which of the following statements are true?<br>a) An infinite number of chords may be drawn for a circle b) One and only one tangent can be drawn to a circle from a point outside it c) An infinite number of diameters may be drawn for a circle d) Every circle has a unique diameter e) Two semi-circles of a circle together make the whole circle<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/ICSE%20-%20Class%2010%20/5fb79e472282923f071fae24">
Question 29 :
Which of the following statements are true?<br>a) Atmost one common tangent can be drawn for any two concentric circles b) Atmost two common tangents can be drawn touching any two circles c) A maximum of four common tangents can be drawn touching any two circles d) Atmost three common tangents can be drawn touching two circles which touch each other<br>
Question 30 :
If two circles touch internally, the number of their common tangents is