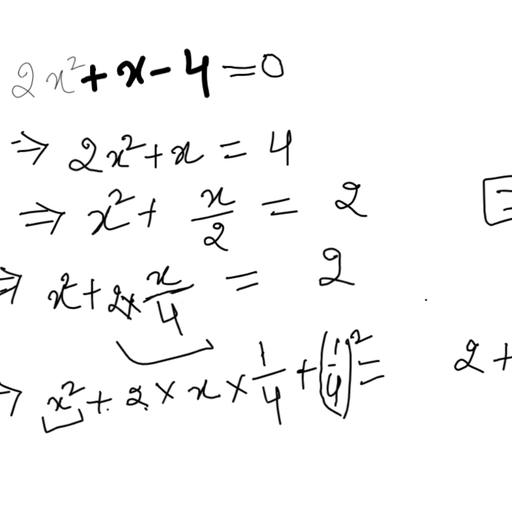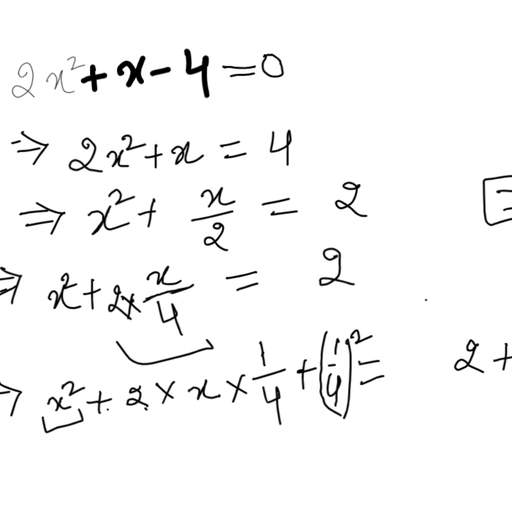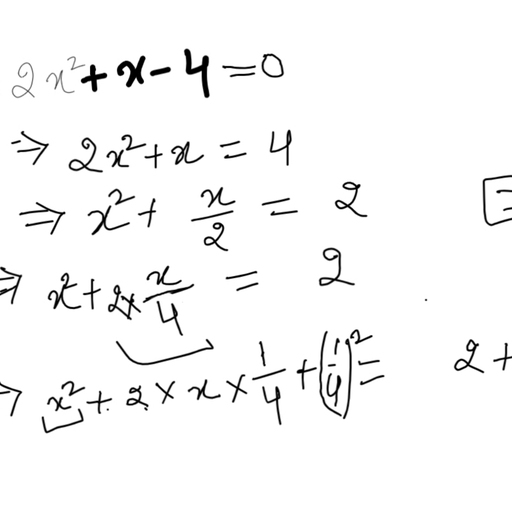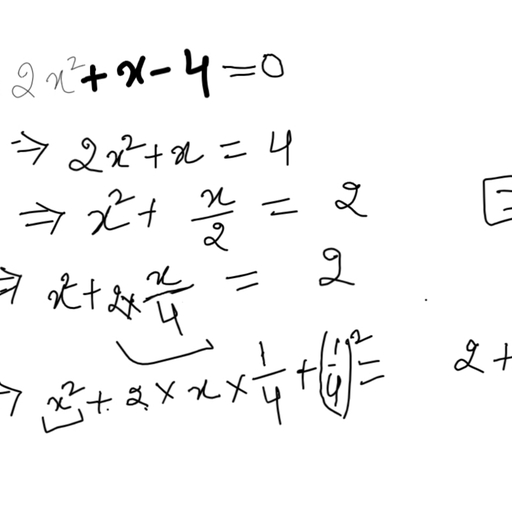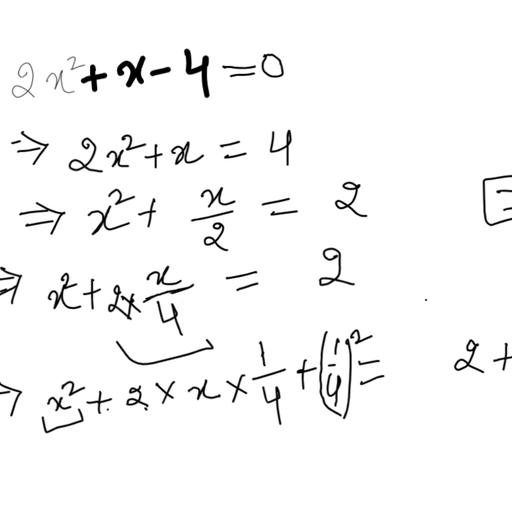Question 1 :
A fraction becomes $\frac{9}{11}$, if 2 is added to both the numerator and the denominator.If, 3 is added to both the numerator and the denominator it becomes $\frac{5}{6}$. Find the fraction.
Question 2 :
Solve the following pair of linear equations by the elimination method and the substitution method : $\frac{x}{2}+\frac{2y}{3}=-1 ~and~ x-\frac{y}{3}=3$
Question 3 :
On comparing the ratios $\frac{a_1}{a_2]$, $\frac{b_1}{b_2}$ and $\frac{c_1}{c_2}$, find out whether the lines representing a pair of linear equations are consistent or inconsistent: $\frac{3}{2}x + \frac{5}{3}y = 7 ; 9x – 10y = 14$
Question 4 :
In the following pair of equations: 2x + y = 6 and 2x – y + 2 = 1, find the ratio of the areas of the two triangles formed by the lines representing these equations with the x-axis and the lines with the y-axis.
Question 5 :
Solve the following pair of equations by reducing them to a pair of linear equations : $\frac{7x-2y}{xy} = 5 ; \frac{8x+7y}{xy} = 15$.
Question 6 :
State whether the following pair of linear equations has unique solution, no solution, or infinitely many solutions : $x – 3y – 3 = 0 ; 3x – 9y – 2 = 0$
Question 8 :
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” Which of these represent this situation algebraically?
Question 9 :
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Question 10 :
The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is Rs. 105 and for a journey of 15 km, the charge paid is Rs. 155. What are the fixed charges and the charge per km?
Question 11 :
Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Question 12 :
Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed are intersecting lines.
Question 13 :
Solve the following pair of equations by reducing them to a pair of linear equations : $6x + 3y = 6xy ; 2x + 4y = 5xy$.
Question 14 :
Solve the following pair of linear equations by the substitution method : $3x – y = 3 ; 9x - 3y = 9$
Question 15 :
If the lines are represented by the equation $a_1x + b_1y + c_1 =0$ and $a_2x + b_2y + c_2 =0$, then the lines are intersecting when _____________.
Question 16 :
A pair of linear equations which has no solution, is called an __________________ pair of linear equations.
Question 17 :
Solve the following pair of equations by reducing them to a pair of linear equations : $\frac{5}{x-1} + \frac{1}{y-2} = 2 ; \frac{6}{x-1} - \frac{3}{y-2} = 1$.
Question 18 :
Romila went to a stationery shop and purchased 2 pencils and 3 erasers for Rs. 9. Her friend Sonali saw the new variety of pencils and erasers with Romila, and she also bought 4 pencils and 6 erasers of the same kind for Rs. 18. Which of these represent this situation algebraically ?
Question 20 :
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid Rs. 27 for a book kept for seven days, while Susy paid Rs. 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Question 21 :
On comparing the ratios $\frac{a_1}{a_2]$, $\frac{b_1}{b_2}$ and $\frac{c_1}{c_2}$, find out whether the lines representing a pair of linear equations are consistent or inconsistent: $3x + 2y = 5 ; 2x – 3y = 7$
Question 22 :
State whether the following pair of linear equations has unique solution, no solution, or infinitely many solutions : $3x – 5y = 20 ; 6x – 10y = 40$
Question 23 :
Solve the following pair of equations by reducing them to a pair of linear equations : $\frac{1}{3x+y} + \frac{1}{3x-y} = \frac{3}{4} ; \frac{1}{2(3x+y)} - \frac{1}{2(3x-y)} = \frac{-1}{8}$.
Question 24 :
Meena went to a bank to withdraw Rs. 2000. She asked the cashier to give her Rs. 50 and Rs. 100 notes only. Meena got 25 notes in all. Find how many notes of Rs. 50 and Rs. 100 she received.
Question 25 :
For which value of k will the following pair of linear equations have no solution? $3x + y = 1; (2k – 1)x + (k – 1) y = 2k + 1$