Question 1 :
Represent the following situation in the form of quadratic equations: A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.

Question 2 :
Find the roots of the following quadratic equation by factorisation: $2x^2 + x – 6 = 0$

Question 3 :
The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.

Question 4 :
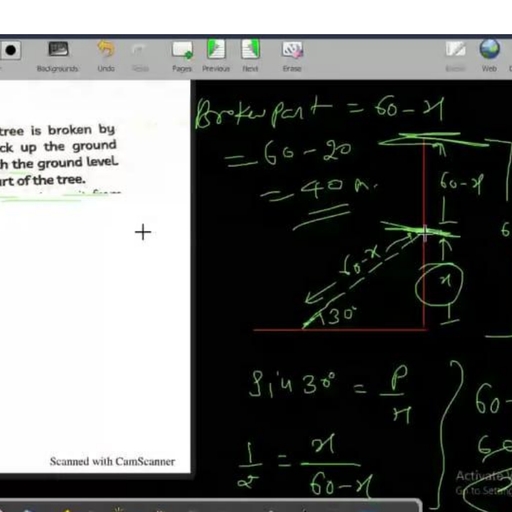
The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.

Question 5 :
Check whether the following is a quadratic equation: $(x + 1)^2 = 2(x – 3)$

Question 6 :
Check whether the following is a quadratic equation: $x^2 + 3x + 1 = (x – 2)^2$

Question 7 :
Find the roots of the quadratic equations, if they exist, by the method of completing the square: $2x^2 + x + 4 = 0$

Question 8 :
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11km/h more than that of the passenger train, find the average speed of the passenger train.

Question 9 :
Is it possible to design a rectangular park of perimeter 80 m and area $400 m^2$ ? If so, find its length and breadth.

Question 10 :
In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.

Question 11 :
Find the roots of the quadratic equations, if they exist, by applying quadratic formula: $2x^2 – 7x + 3 = 0$

Question 12 :
Find the nature of the roots of the following quadratic equation: $2x^2 – 6x + 3 = 0$

Question 13 :
Find two numbers whose sum is 27 and product is 182.

Question 14 :
Find the roots of the following quadratic equation: $2x^2 – 6x + 3 = 0$.

Question 15 :
Find the roots of the following quadratic equation by factorisation: $x^2 – 3x – 10 = 0$

Question 16 :
Find the values of k for each of the following quadratic equations, so that they have two equal roots: $kx (x – 2) + 6 = 0$

Question 17 :
Is it possible to design a rectangular mango grove whose length is twice its breadth,and the area is $800 m^2$ ? If so, find its length and breadth.

Question 18 :
Find the roots of the quadratic equations, if they exist, by the method of completing the square: $2x^2 + x – 4 = 0$

Question 19 :
A cottage industry produces a certain number of toys in a day. The cost of production of each toy (in rupees) was found to be 55 minus the number of toys produced in a day. On a particular day, the total cost of production was Rs. 750. Find out the number of toys produced on that day.