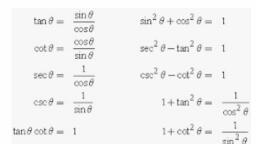Question 1 :
Which of the following is equal to $\sin x \sec x$?
Question 2 :
Given $tan \theta = 1$, which of the following is not equal to tan $\theta$?
Question 3 :
$\tan \theta$ increases as $\theta$ increases.<br/>If true then enter $1$ and if false then enter $0$.<br/>
Question 4 :
Select and wire the correct answer from the given alternatives. <br/>$\cos \left(\dfrac {3\pi}{2}+\theta \right)=$ ____
Question 5 :
If $sin({ 90 }^{ 0 }-\theta )=\dfrac { 3 }{ 7 } $, then $cos\theta $
Question 7 :
The value of $\sqrt { 3 } \sin { x } +\cos { x } $ is max. when $x$ is equal to
Question 9 :
Simplest form of $\displaystyle \dfrac{1}{\sqrt{2 + \sqrt{2 + \sqrt{2 + 2 cos 4x}}}}$ is
Question 11 :
As value of $x$ increases from $0$ to $\cfrac{\pi}{2}$, the value of $\cos {x}$:
Question 12 :
Solve:$\displaystyle \sin ^{4}\theta +2\cos ^{2}\theta \left ( 1-\frac{1}{\sec ^{2}\theta } \right )+\cos ^{4}\theta $
Question 13 :
Eliminate $\theta$ and find a relation in x, y, a and b for the following question.<br/>If $x = a sec \theta$ and $y = a tan \theta$, find the value of $x^2 - y^2$.
Question 14 :
If $sec\theta -tan\theta =\dfrac{a}{b},$ then the value of $tan\theta $ is
Question 17 :
Choose the correct option. Justify your choice.<br/>$\displaystyle 9{ \sec }^{ 2 }A-9{ \tan }^{ 2 }A=$<br/>
Question 19 :
If $\sec{2A}=\csc{(A-42^\circ)}$ where $2A$ is acute angle then value of $A$ is
Question 20 :
If $\sin \theta + \cos\theta = 1$, then what is the value of $\sin\theta \cos\theta$?