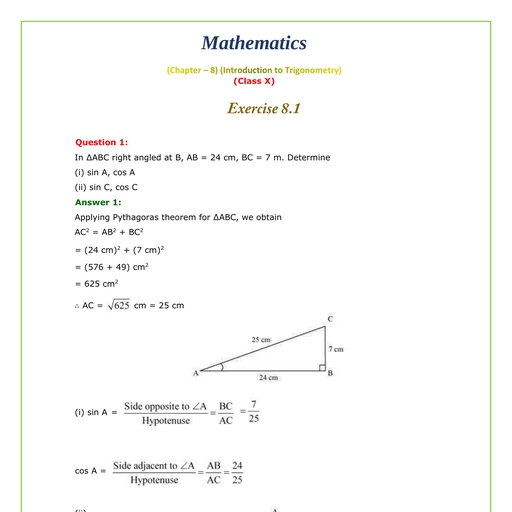
Question 1 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b19b91273b2305849799cd.jpg' />
Total surface area of a lattu (top) as shown in the above figure is the sum of total surface area of hemisphere and the total surface area of cone.
Question 2 :
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter $l$ of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Question 3 :
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest $cm^2$.
Question 4 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b19c35273b230584979a94.JPG' />
In the above image, hanumappa and his wife Gangamma are busy making jaggery out of sugarcane juice. They have processed the sugarcane juice to make the molasses, which is poured into moulds in the shape of a frustum of a cone having the diameters of its two circular faces as 30 cm and 35 cm and the vertical height of the mould is 14 cm (see the above image). If each cubic cm of molasses has mass about 1.2 g, find the mass of the molasses that can be poured into each mould. (Take $\pi$ =$\frac{22}{7}$)
Question 5 :
A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 $cm^3$ of iron has approximately 8 g mass. (Use $\pi$ = 3.14)
Question 6 :
What is the formulae for volume of a spherical shell?(where $r_1$ and $r_2$ are respectively its external and internal radii)
Question 7 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b19c33273b230584979a92.JPG' />
The radii of the ends of a frustum of a cone 45 cm high are 28 cm and 7 cm (see the above image). Find its volume(Take $\pi$ = $\frac{22}{7}$ ).
Question 8 :
A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
Question 9 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b19b95273b2305849799d2.jpg' />
Two solid cones A and B are placed in a cylinderical tube as shown in the above figure.The ratio of their capacities are 2:1 and 6 cm is the diameter of cone.Find the volume of the remaining portion of the cylinder. (i.e. the portion excluding the cones)
Question 11 :
The curved surface area of a frustum of a cone is $\pi l\left(r_1+r_2\right)$, where l=$\sqrt{h^2+r_1^2+r_2^2}$ , $r_1$ and $r_2$ are the radii of the two ends of the frustum and h is the vertical height.
Question 12 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b19b92273b2305849799ce.jpg' />
Actual capacity of a vessel as shown in the above figure is equal to the difference of volume of the cylinder and volume of the hemisphere.
Question 13 :
16 glass spheres each of radius 2 cm are packed into a cuboidal box of internal dimensions 16 cm × 8 cm × 8 cm and then the box is filled with water. Find the volume of water filled in the box.
Question 14 :
A spherical steel ball is melted to make eight new identical balls.Then, the radius of each new ball be $\frac{1}{8}$th the radius of the original ball.
Question 15 :
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs 20 per litre.
Question 16 :
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length of the wire, assuming the density of copper to be 8.88 g per $cm^3$ .
Question 17 :
A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diameter and height of the cylinder are 6 cm and 12 cm, respectively. If the the slant height of the conical portion is 5 cm, find the volume and total surface area of the rocket.
Question 18 :
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that $\frac{1}{8}$ space of the cube remains unfilled. Then the number of marbles that the cube can accomodate is
Question 19 :
The volume of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
Question 20 :
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
Question 21 :
How many shots each having diameter 3 cm can be made from a cuboidal lead solid of dimensions 9cm × 11cm × 12cm?
Question 22 :
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
Question 23 :
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Question 24 :
A right circular cylinder of radius r cm and height h cm (h>2r) just encloses a sphere of diameter
Question 25 :
A metallic right circular cone 20 cm high and whose vertical angle is $60^{\circ}$, is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter $\frac{1}{16}$ cm, then find the length of the wire.
Question 26 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b19c3a273b230584979a9a.JPG' />
In the above diagram, a gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm
Question 27 :
A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume of the double cone so formed.
Question 28 :
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm.
Question 29 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b19c30273b230584979a8e.JPG' />
In the above image, shanta runs an industry in a shed which is in the shape of a cuboid surmounted by a half cylinder as shown. If the base of the shed is of dimension 7 m × 15 m, and the height of the cuboidal portion is 8 m, then find the volume of air that the shed can hold. (Take $\pi$ = $\frac{22}{7}$ )
Question 30 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b19b90273b2305849799cb.jpg' />
In the above figure, plumbline (sahul) is the combination of
Question 31 :
Water is flowing at the rate of 15 km/h through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in pond rise by 21 cm?
Question 32 :
A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Question 33 :
A cubical block of side 7 cm is surmounted by a hemisphere.Find the surface area of the solid.
Question 34 :
The volume of the frustum of a cone is $\frac{1}{3}\pi h\left[r_1^{2}+r_2^{2}-r_1r_2\right]$, where h is vertical height of the frustum and $r_1, r_2$ are the radii of the ends.
Question 35 :
A canal is 300 cm wide and 120 cm deep. The water in the canal is flowing with a speed of 20 km/h. How much area will it irrigate in 20 minutes if 8 cm of standing water is desired?
Question 37 :
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the mass of the wire, assuming the density of copper to be 8.88 g per $cm^3$.
Question 38 :
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Question 39 :
How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Question 40 :
Selvi’s house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57 m × 1.44 m × 95cm. The overhead tank has its radius 60 cm and height 95 cm. Find the height of the water left in the sump after the overhead tank has been completely filled with water from the sump which had been full. (Use $\pi$ = 3.14)
Question 41 :
A toy is in the form of a cone of radius 3.5 cm surmounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Question 42 :
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. (Note that the base of the tent will not be covered with canvas.)
Question 43 :
How many spherical lead shots of diameter 4 cm can be made out of a solid cube of lead whose edge measures 44 cm.
Question 44 :
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Question 45 :
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Question 46 :
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base. Compare the volumes of the two parts.
Question 47 :
A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in his field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/hr, in how much time will the tank be filled?
Question 48 :
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open is 5 cm. It is filled with water upto brim. When lead shots each in the shape of a sphere with radius 0.5 cm are dropped into the vessel, the one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Question 49 :
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
Question 50 :
A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm, 5 cm and 4 cm. The radius of each the conical depressions is 0.5 cm and the depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand.