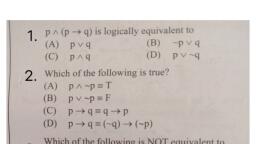Question 1 :
If quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.<br/>
Question 3 :
$x + 2x + 3x = M$ find value of M
Question 4 :
State whether the following statement is True or False.<br>The product of two even numbers is always even.<br>
Question 6 :
Select and write the correct answer from the given alternative of the following question:<br>If $ p \wedge q $ is F , $ p \rightarrow q $ is F then the truth values of $p$ and $q$ are ___________.
Question 8 :
State whether the following statement is True or False.<br>The sum of two odd numbers and one even number is even.<br>
Question 10 :
Here are some words translated from an artificial language<br/>$ mie \ pie \ is \ blue \ light$<br/>$ mie \ tie \ is \ blue \ berry$<br/><span>$ aie \ tie \ is \ rasp \ berry$<br/></span><span>Which words could possibly mean "light fly"?<br/></span>
Question 13 :
$3x + 2x = 5P$, what will come at place of P
Question 14 :
Assertion: Two distinct lines cannot have more than one point in common.
Reason: Any number of lines can be drawn through one point.
Question 15 :
State whether the following statement is True or False.<br>The sum of three odd numbers is even.<br>
Question 16 :
<span>Check if the given statement is true or false.</span><div>$x(3x + 2) = 3x^2 + 2$</div>
Question 17 :
Select and write the correct answer from the given alternative of the following question:<br>If $ p \wedge q $ is false and $ p \wedge q $ is true, then __________ is not true.
Question 18 :
Consider the sentence: x<5 <br>Which of the following integers makes this open sentence true?
Question 19 :
If truth values of $p$ be $F$ and $q$ be $T$. Then, truth value of $\sim (\sim p\vee q)$ is
Question 21 :
If $p, q, r$ are simple proportions with truth values $T, F, T$, then the truth value of $(\sim p\vee q)\wedge \sim r \Rightarrow p$ is
Question 22 :
If $p$ and $q$ are two statements then $(p \leftrightarrow \sim q)$ is true when
Question 23 :
What is the truth value of the statement 'Two is an odd number iff 2 is a root of $x^2+2=0$'?
Question 24 :
Write the negation of the statement "If the switch is on<span>, then the fan rotates".</span>
Question 27 :
Which one of the following statements is not a false statement?<br>
Question 28 :
Consider the following statements<br>$P:$Suman is brilliant<br>$Q:$Suman is rich<br>$R:$Suman is honest.<br>The negative of the statement."Suman is brilliant and dishonest, if and only if Suman is rich" can be expressed as
Question 29 :
Consider the statements<span> <br>(i)Two plus three is five.<br>(ii) Every square is a rectangle.<br>(iii) Sun rises in the east.<br>(iv) The earth is not a star. <br><span>Which of the above statements have truth value (T) ?<br></span></span>
Question 31 :
The statement pattern $(p\wedge q)\wedge [\sim r\vee (p\wedge q)]\vee (\sim p\wedge q)$ is equivalent to _________.
Question 34 :
The converse of: "If two triangles are congruent then they are similar" is<br/>
Question 35 :
Which of the following is negation of the statement <span>"All birds can fly".</span>
Question 36 :
Find the negation of the statement, "Some odd numbers <span>are not prime".</span>
Question 38 :
The dual of the following statement "Reena is healthy and Meena is beautiful" is
Question 39 :
Find the truth value of the compound statement, 4 is the first composite number and $2+5=7$.
Question 40 :
Let $f$ be a function from a set $X$ to a set $Y$.<br/>Consider the following statements<br/>$P:$ For each $x\epsilon X$, there exists unique $y\epsilon Y$ such that $f(x) = y$.<br/>$Q:$ For each $y\epsilon Y$, these exists $x\epsilon X$ such that $f(x) = y$.<br/>$R:$ There exist $x_{1}, x_{2}\epsilon X$ such that $x_{1}\neq x_{2}$ and $f(x_{1}) = f(x_{2})$<br/>The negation of the statement $"f$ is one-to-one and onto" is
Question 41 :
If $p$'s truth value is $T$ and $q$'s truth value is $F$, then which of the following have the truth value $T$?<br>(i) $p\vee q$<br>(ii) $\sim p\vee q$<br>(iii) $p\vee (\sim q)$<br>(iv) $p\wedge (\sim q)$
Question 43 :
If $p\rightarrow (q \vee r)$ is false, then the truth values of $p,q,r$ are respectively<br/>
Question 44 :
Assertion: STATEMENT 1:$\sim(p \leftrightarrow \sim q)$ is equivalent to $(p\vee \sim q) \wedge (\sim p\vee q)$
Reason: STATEMENT 2: $\sim(p \leftrightarrow q)$ is equivalent to $(p \wedge \sim q) \vee (\sim p \wedge q)$
Question 45 :
If $p, q$ are two distinct primes, then $\sigma (pq)$ equals (where the operation $\sigma$ on a number $n$ is defined as the sum of all divisors of the number $n$.)<br>
Question 46 :
The contrapositive of the statement 'If I am not feeling well, then I will go to the doctor' is:
Question 48 :
Consider statement " If I do not work, I will sleep. If I am worried, I will not sleep. Therefore if I am worried, I will work". This statement is
Question 49 :
Negation of "Ram is in class $X$ or Rashmi is in class $XII$" is
Question 50 :
Consider the statements:<div>(i) Sun rises or moon sets.</div><div>(ii) All integers are positive or negative.<br/>(iii) Two lines intersect at a point or are parallel.<br/>(iv) The school is closed if it is a holiday or a Sunday.<br/>Which of the above statements is inclusive or statement?<br/></div>