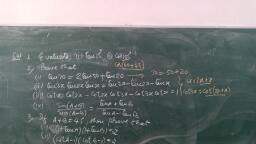Question 1 :
Let $A = \left \{x, y, z\right \}$ and $B = \left \{p, q, r, s\right \}$. What is the number of distinct relations from $B$ to $A$?

Question 3 :
Let R be the set of real numbers and the mapping $f:R\rightarrow R$ and $g:R\rightarrow R$ be defined by $f(x)=5-x^2$ and $g(x)=3\lambda-4$, then the value of $(fog)(-1)$ is

Question 4 :
Classify the following set as 'singleton' or 'empty':  $B = \{y | y$ is an odd prime number $< 4\}$

Question 6 :
State the whether given statement is true or falseIf $A$ is any set, prove that: $A\subseteq \phi \Leftrightarrow A=\phi $.

Question 7 :
Let $A$ $=$ set of all cuboids and B $=$ set of all cubes. Which of the following is true?

Question 9 :
In a survey of 25 students, it was found that 15 had taken mathematics, 12 had taken physics and 11 had taken chemistry, 5 had taken mathematics and chemistry, 9 had taken mathematics and physics, 4 had taken physics and chemistry and 3 had taken all the three subjects.Find the number of students that had taken none of the subjects.

Question 10 :
If $S$ is a set with $10$ elements and $A = \left \{(x, y) : x, y\epsilon S, x\neq y\right \}$, then number of elements in $A$ is

Question 11 :
State whether the following statement is true or false.<br>$a\subset \{b, c, a\}$.<br>

Question 12 :
The solution set of $x+2&lt;9$ over a set of positive even integers is&#160;

Question 13 :
In a survey of 25 students, it was found that 15 had taken mathematics, 12 had taken physics and 11 had taken chemistry, 5 had taken mathematics and chemistry, 9 had taken mathematics and physics, 4 had taken physics and chemistry and 3 had taken all the three subjects.Find the number of students that had taken exactly two&#160;of the three subjects.

Question 14 :
If $\displaystyle \sin B=\frac{1}{2}$ what is the value of $\displaystyle 3\cos B-4\cos ^{3}B?$

Question 16 :
Given that&#160;$ \displaystyle \cos 50^{\circ}18'=0.6388\ and\ \cos 50^{\circ}42'=0.6334, $ then the possible value of&#160;$ \displaystyle \cos 50^{\circ}20' $ is&#160;

Question 17 :
If tan A = 4 /3, tanB = 1/ 7,then A - B =

Question 20 :
Find the value of $\displaystyle&#160;\frac { \sqrt { 1+\sin { 2A } &#160;} +\sqrt { 1-\sin { 2A } &#160;} &#160;}{ \sqrt { 1+\sin { 2A } &#160;} -\sqrt { 1-\sin { 2A } &#160;} &#160;} $ when $\left| \tan { A } &#160;\right| &lt;1$ and $\left| A \right| $ is acute

Question 21 :
A wheel makes $240$ revolutions in one minute The measure of the angle it describes at the centre in $15$ seconds is ___&#160;<br/>

Question 23 :
If $\alpha$ is a root of $25\cos^2\theta +5\cos \theta =0, \dfrac{\pi}{2} &lt; \alpha &lt; \pi$, then $\sin^2\alpha$ is equal to-

Question 24 :
The degree measure of 1 radian (taking $\pi =\dfrac { 22 }{ 7 }$ ) is

Question 29 :
If $\left( \dfrac{1 + i}{1 - i} \right)^m = 1$, then the least positive integral value of m is