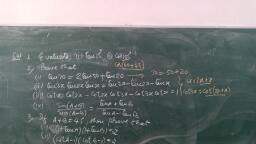Question 1 :
If A, B, C be three sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C, then

Question 2 :
If A and B are sets, then A ∩ (B - A) is

Question 3 :
Let A = {a, b, c} and B = {1, 2}. Consider a relation R defined from set A to set B. Then R is equal to set

Question 4 :
In a city 20 percent of the population travels by car, 50 percent travels by bus and 10 percent travels by both car and bus. Then persons travelling by car or bus is

Question 5 :
The set $\left( A\cap { B }^{ C } \right) ^{ C }\cup \left( B\cap C \right) $ is equal to

Question 6 :
If {tex} 8 i z ^ { 3 } + 12 z ^ { 2 } - 18 z + 27 i = 0 , {/tex} then

Question 7 :
If {tex} z = x + i y {/tex} and {tex} x ^ { 2 } + y ^ { 2 } = 16 , {/tex} then the range of {tex} || x | - | y|| {/tex} is

Question 8 :
If {tex} z ^ { 2 } + z + 1 = 0 , {/tex} where {tex} z {/tex} is a complex number, then the value of {tex} \left( z + \frac { 1 } { z } \right) ^ { 2 } + \left( z ^ { 2 } + \frac { 1 } { z ^ { 2 } } \right) ^ { 2 } {/tex} {tex} + \left( z ^ { 3 } + \frac { 1 } { z ^ { 3 } } \right) ^ { 2 } + \ldots + \left( z ^ { 6 } + \frac { 1 } { z ^ { 6 } } \right) ^ { 2 } {/tex} is

Question 9 :
If {tex} \frac { \left( x ^ { 2 } - 1 \right) ( x + 2 ) ( x + 1 ) ^ { 2 } } { ( x - 2 ) } < 0 , {/tex} then {tex} x {/tex} lies in the interval

Question 10 :
$ \sin A(1+\tan A) + \cos A(1+\cot A) = \sec A + \text{cosec} A.$

Question 11 :
In $\sin \theta = \dfrac{{ - 1}}{{\sqrt 2 }}\&amp; \;\tan \;\theta $ lies in which quadrant?

Question 12 :
If $\theta$ is in the first quadrant and cos $\theta=\frac{3}{5}$, then the value of $\dfrac{5 tan \theta -4cosec \theta}{5 sec\theta-4cot \theta}$ is<br/><br/>

Question 13 :
A pole stands vertically inside a triangular park &Delta;ABC. If the angle of elevation of the top of the pole from each corner of the park is same, then in &Delta; ABC the foot of the pole is at the

Question 14 :
What will be the values of $\theta$ between $0^\circ$ and $360^\circ$ if $\displaystyle\sin{\theta}=-\frac{\sqrt{3}}{2}$

Question 15 :
The value of a for which the equation 4cosec²(&pi; (a + x)) + a² - 4a = 0 has a real solution, is

Question 16 :
The angle of elevation of the top of a tower at a distance of 500 meter from the foot is $ \displaystyle30^{\circ} $ , the height of the tower is

Question 18 :
If the length of the sides of a triangle are 3, 4 and 5 units, then R (the circum-radius) is

Question 19 :
If roots of equation x³ - 12x² + 39x - 28 = 0 are in A.P. then common difference =

Question 20 :
If <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e8728ff19f8d44d3a1806ab' height='39' width='172' >, then the value of n is