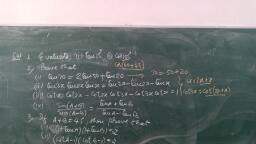Test Details

Practice Test 3

Term 1

Jan 10, 10:15 AM

30 minutes

Jan 10, 10:45 AM

40.0 marks

MCQ

30 questions

I Sir

25 years of excellence

Class Details

Mathematics

SXC Ali Maths11D 23

Mathematics

More from I Sir

(20)

Test

Trigonometry

class-11th

Mathematics

0 Likes

0 Views

I Sir

Feb 03, 2022

Test

Trigonometry

class-11th

Mathematics

0 Likes

0 Views

I Sir

Feb 01, 2022

Homework

Trigonometric Equations

class-11th

Mathematics

0 Likes

16 Views

I Sir

Jan 31, 2022

Test

Practice Test 6

class-11th

Mathematics

0 Likes

0 Views

I Sir

Jan 27, 2022

Test

Practice Test 6

class-11th

Mathematics

0 Likes

0 Views

I Sir

Jan 27, 2022

Test

Practice Test 6

class-11th

Mathematics

0 Likes

3 Views

I Sir

Jan 27, 2022

Test

Practice Test 5

class-11th

Mathematics

0 Likes

2 Views

I Sir

Jan 22, 2022

Test

Practice Test 4

b-sc

Mathematics

0 Likes

4 Views

I Sir

Jan 21, 2022

Test

Practice Test 4

class-11th

Mathematics

0 Likes

2 Views

I Sir

Jan 18, 2022

Test

PCT 4 Level 2

b-sc

Mathematics

0 Likes

4 Views

I Sir

Jan 10, 2022

Test

Practice Test 3

class-11th

Mathematics

0 Likes

0 Views

I Sir

Jan 10, 2022

Test

Practice Test 3

class-11th

Mathematics

0 Likes

0 Views

I Sir

Jan 10, 2022

Test

Practice Test 3

class-11th

Mathematics

0 Likes

3 Views

I Sir

Jan 07, 2022

Test

Mock Practice 2

class-11th

Mathematics

0 Likes

0 Views

I Sir

Jan 07, 2022

Test

Mock Practice 2

class-11th

Mathematics

0 Likes

4 Views

I Sir

Jan 07, 2022

Test

Practice Test 1

class-11th

Mathematics

0 Likes

4 Views

I Sir

Jan 06, 2022

Test

Term 1 : Trigonometry

class-11th

Mathematics

0 Likes

24 Views

I Sir

Dec 21, 2021

Test

Maths Contest 22

b-sc

Mathematics

0 Likes

38 Views

I Sir

Dec 17, 2021

Homework

Compound Angles

class-11th

Mathematics

0 Likes

48 Views

I Sir

Nov 23, 2021

Test

Trigonometry

class-11th

Mathematics

0 Likes

20 Views

I Sir

Nov 08, 2021

Recommended Content

(20)

Test

Practice Test 4

class-2nd

Mathematics

0 Likes

4 Views

Imtiyaz Ali

Jan 21, 2022

Test

Practice Set -1

class-11th

Chemistry

0 Likes

28 Views

Harikesh Sir

Nov 10, 2021

Test

Practice Test 3

class-11th

Mathematics

0 Likes

0 Views

Imtiyaz Ali

Jan 10, 2022

Test

Practice Test 3

class-11th

Mathematics

0 Likes

0 Views

Imtiyaz Ali

Jan 10, 2022

Test

Practice Test 4

class-11th

Mathematics

0 Likes

2 Views

Imtiyaz Ali

Jan 18, 2022

Test

Practice Test 1

class-11th

Mathematics

0 Likes

4 Views

Imtiyaz Ali

Jan 06, 2022

Test

Practice MCQ 3

class-11th

Financialaccounting

0 Likes

24 Views

Ayush Aggarwal

Nov 23, 2021

Test

Practice Test 5

class-11th

Mathematics

0 Likes

2 Views

Imtiyaz Ali

Jan 22, 2022

Test

Practice Test 3

b-sc

Mathematicssecd

0 Likes

0 Views

Imtiyaz Ali

Jan 10, 2022

Test

Practice Test 3

b-sc

Mathematicssecd

0 Likes

0 Views

Imtiyaz Ali

Jan 10, 2022

Test

Practice Test 3

b-sc

Mathematicssecd

0 Likes

0 Views

Imtiyaz Ali

Jan 10, 2022

Test

Practice Test 3

b-sc

Mathematicssecd

0 Likes

3 Views

Imtiyaz Ali

Jan 10, 2022

Test

Mock Practice 2

class-11th

Mathematics

0 Likes

0 Views

Imtiyaz Ali

Jan 07, 2022

Test

Mock Practice 2

class-11th

Mathematics

0 Likes

4 Views

Imtiyaz Ali

Jan 07, 2022

Test

Practice Test 1

b-sc

Mathematics

0 Likes

0 Views

Imtiyaz Ali

Jan 06, 2022

Test

Practice Test 4

b-sc

Mathematics

0 Likes

4 Views

Imtiyaz Ali

Jan 21, 2022

Test

PRACTICE

class-9th

Mathematics

0 Likes

11 Views

FRINDLY GAMERS

Nov 21, 2021

Homework

Practice Test 4

class-12th

English

0 Likes

75 Views

Krishna Singh

Nov 27, 2021

Test

Practice MCQ 6

class-11th

Financialaccounting

0 Likes

15 Views

Ayush Aggarwal

Nov 23, 2021

Test

Practice MCQ 4

class-11th

Financialaccounting

0 Likes

16 Views

Ayush Aggarwal

Nov 23, 2021

Question Text

Question 1 :
If X and Y are two sets such that $n(X)=45, n(X \cup Y)=76, n(X \cap Y)=12,$ find $n(Y)$.

Question 2 :
Given $K=\left \{B, A, N, T, I\right \}$. Then the number of subsets of K, that contain both A, N is

Question 3 :
$25$ people for applied for programme $A$, $50$ people for programme $B$, $10$ people for both. So number of employee applied only for $A$ is

Question 4 :
If  $D = \{q|(q-4)^2 = 0\}$ then the set $D$ is a 

Question 6 :
If $\displaystyle R=\{ (x,y):x, y \in Z ,x^{2}+y^{2}\leq 4 \}$ is a relation in $Z$ then domain $D$ is

Question 7 :
Let $A=\left\{ x\in W,the\quad set\quad of\quad whole\quad numbers\quad and\quad x<3 \right\} $ $B=\left\{ x\in N,the\quad set\quad of\quad natural\quad numbers\quad and\quad 2\le x<4 \right\} $ and $C=\left\{ 3,4 \right\} $, then how many elements will $\left( A\cup B \right) \times C$ conatin?

Question 8 :
$A = \left \{1, 2, 3, 4\right \}$ and $B = \left \{a, b, c\right \}$. The relations from $A$ to $B$ is

Question 9 :
If A and B are two non-empty sets having n elements in common, then what is the number of common elements in the sets $A\times B$ and $B\times A$?

Question 10 :
A is a set having $6$ distinct elements. The number of distinct function from A to A which are not bijections is?

Question 11 :
If $x\cos { { 60 }^{ o } } -y\cos { { 0 }^{ o } } =3$ $4x\sin { { 360 }^{ o } } -y\cot { { 45 }^{ o } } =2$ then what is the value of $x$?

Question 12 :
If $\tan 45^{\circ} = \cot \theta$, then the value of $\theta$, in radians is

Question 14 :
If tan A = 4 /3, tanB = 1/ 7,then A - B =

Question 15 :
If $ \displaystyle \tan \Theta =2-\sqrt{3}$,then $ \tan \left ( 90^{\circ}-\Theta \right ) $ is equl to

Question 17 :
$A+B=\cfrac { \pi }{ 3 } ;\cos { A } +\cos { B } =1$, value of $\left| \cos { A } -\cos { B } \right| $ is

Question 18 :
The value of $\cfrac { \tan ^{ 2 }{ { 60 }^{ o } } -2\tan ^{ 2 }{ { 45 }^{ o } } +\sec ^{ 2 }{ { 30 }^{ o } }  }{ 3\sin ^{ 2 }{ { 45 }^{ o } } \sin { { 90 }^{ o } } +\cos ^{ 2 }{ { 60 }^{ o } } \cos ^{ 3 }{ { 0 }^{ o } }  } $ is

Question 20 :
The angles of a triangle are in $A.P.$. The number of degree in the least is to be the number of radians in the greatest as $60:\pi$. Then the greatest angle is

Question 21 :
The argument of $\displaystyle \frac{(1 - i \sqrt 3)}{(1 + i \sqrt 3)}$ is

Question 22 :
If $u = 3 - 5i$ and $v = -6 + i$, then the value of $(u+v)^2$ is

Question 24 :
Two complex numbers are represented by ordered pairs $z_1: (a,b)\ \&\ z_2: (c,d)$, when these two complex numbers are equal?

Question 26 :
Find the wrong term in sequence :7, 15, 33, 69, 149, 307

Question 27 :
Find the next number in the series. $3, 6, 9, 12, 15,....$

Question 29 :
If the $n^{th}$ term of a sequence is $100n + 10$, then the sequence is

More from I Sir

Recommended Content

Learn from Anywhere on Any Device