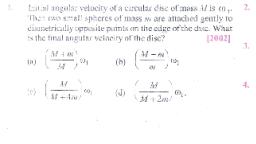Question 1 :
Let {tex} A {/tex} and {tex} B {/tex} are two points outside a circle {tex} S {/tex} such that the chord of contact from {tex} A {/tex} to {tex} S {/tex} passes through {tex} B {/tex}. If the length of tangent from {tex} A {/tex} to {tex} S {/tex} is {tex} l _ { 1 } {/tex} and length of tangent from {tex} B {/tex} to {tex} S {/tex} is {tex} l _ { 2 } , {/tex} then length of {tex} A B {/tex} is
Question 2 :
Let {tex} A B {/tex} be a chord of the circle {tex} x ^ { 2 } + y ^ { 2 } = r ^ { 2 } {/tex} subtending a right angle at the centre. Then the locus of the centroid of the triangle {tex} PAB {/tex} as {tex}P{/tex} moves on the circle is
Question 3 :
If a circle passes through the point {tex} ( a , b ) {/tex} and cuts the circle {tex} x ^ { 2 } + y ^ { 2 } = k ^ { 2 } {/tex} orthogonally, then the equation of the locus of its centre is
Question 4 :
The equations of the tangents drawn from the origin to the circle {tex} x ^ { 2 } + y ^ { 2 } - 2 r x - 2 h y + h ^ { 2 } = 0 , {/tex} are
Question 5 :
Let {tex} P Q {/tex} and {tex} R S {/tex} be tangents at the extremities of the diameter {tex} P R {/tex} of a circle of radius {tex} r {/tex}. If {tex} P S {/tex} and {tex} R Q {/tex} intersect at a point {tex} X {/tex} on the circumference of the circle, then {tex} 2 r {/tex} equals
Question 6 :
A straight line through the point A(-2, -3) cuts the line x + 3y = 9 and x + y + 1 = 0 at B and C respectively. If AB.AC = 20, then equation of the possible line is
Question 7 :
The equation of one of the sides of an isosceles right angled triangle whose hypotenuse is given by 3x + 4y = 4 and the opposite vertex of hypotenuse is (2, 2) is
Question 8 :
Three lines {tex} p x + q y + r = 0 , q x + r y + p = 0 {/tex} and {tex} r x + p y + q = 0 {/tex} are concurrent if
Question 10 :
Equation of a line passing through (1, - 1) and perpendicular to a line given by x<sup>2</sup> - 5xy + 4y<sup>2</sup> = 0 is
Question 11 :
All points lying inside the triangle formed by the points {tex} ( 1,3 ) , ( 5,0 ) {/tex} and {tex} ( - 1,2 ) {/tex} satisfy
Question 12 :
The angle between the lines represented by the equation $ 2x^2 + 3xy - 5y^2 = 0 $ is :
Question 13 :
Assertion (A): The equation $2x^{2}+3xy-2y^{2}+5x-5y+3=0$ represents a pair of perpendicular straight lines.<br/>Reason (R): A pair of lines given by $ax^{2}+2hxy+by^{2}+2gx+2f +c=0$ are perpendicular, if $a+b=0$ <br/>
Question 14 :
The angle between the lines $x\cos \alpha+y\sin\alpha={p}_{1}$ and $x\cos \beta +y\sin \beta=p_{2},$ where $\alpha>\beta$ is<br/>
Question 15 :
The lines joining the origin to the point of intersection of the circle {tex} x ^ { 2 } + y ^ { 2 } = 3 {/tex} and the line {tex} x + y = 2 {/tex} are
Question 16 :
Tow consecutive sides of a parallelogram are $4x + 5y = 0$ and $7x + 2y = 0$.If the equation to one diagonal is $11x + 7y = 9$, then the equation of the other diagonal is <br>
Question 17 :
Assertion: The equation $2x^2 + 3xy - 2y^2 + 5x - 5y + 3 = 0$ represents a pair of perpendicular straight lines.
Reason: A pair of lines given by $ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0$ are perpendicular, if $a + b = 0$
Question 18 :
The lines 3x + 4y = 15 and 4x - 3y = - 36 intersect at P. The first line intersects x-axis at A and the second line intersects y-axis at B, then
Question 19 :
The angle between the lines $kx+y+9=0$, $y-3x =4$ is $45^{o},$ then the value of $k$ is :<br/>
Question 20 :
The quadrilateral $ABCD$ formed by the point $A(0, 0)$; $B(3, 4);$ $C(7, 7)$ and $D(4, 3) $ is a
Question 21 :
If two lines $ax^2+2hxy+by^2=0$ make angles $\alpha$ and $\beta$ with $X-$axis, then the $(\alpha+\beta)=$_____.
Question 22 :
If (<em>α</em>, <em>α</em><sup>2</sup>) lies inside the triangle formed by the lines 2<em>x</em> + 3<em>y</em> − 1 = 0, <em>x</em> + 2<em>y</em> − 3 = 0, 5<em>x</em> − 6<em>y</em> − 1 = 0, then
Question 23 :
Measure of the angle between x + y = 0 and y = 5 is _______.
Question 25 :
$A(p, 0), B(4, 0), C(5, 6)$ and $D(1, 4)$ are the vertices of a quadrilateral $ABCD$. If $\angle ADC$ is obtuse, the maximum integral value of $p$ is :