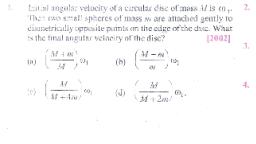Question 1 :
Arrange the values of $n$ in ascending order<br/>A : If the term independent of $x$ in the expansion of $\left(\displaystyle \sqrt{x}-\frac{n}{x^{2}}\right)^{10}$ is $405$<br/>B : If the fourth term in the expansion of $\left(\displaystyle \frac{1}{n}+n^{\log_{n}10}\right)^{5}$ is $1000$, <span>( $ n&lt; 10 $)<br/>C : In the binomial expansion of $(1+x)^{n}$ the coefficients of <span> $5^{\mathrm{t}\mathrm{h}},\ 6^{\mathrm{t}\mathrm{h}}$ and $7^{\mathrm{t}\mathrm{h}}$ terms are in A.P.</span></span><br/>

Question 2 :
If there is a term containing $x^{2r}$ in $\left( x + \dfrac{1}{x^2} \right )^{n - 3}$, then

Question 3 :
Find the coefficient of ${ x }^{ 50 }$ in the expression:<br>${ \left( 1+x \right) }^{ 1000 }+2x{ \left( 1+x \right) }^{ 999 }+3{ x }^{ 2 }{ \left( 1+x \right) }^{ 998 }+....+1001{ x }^{ 1000 }$<br>

Question 4 :
The range of the function $f(\theta )=\sqrt { { 8\sin }^{ 2 }\theta +{ 4\cos }^{ 2 }\theta -8\sin\theta \cos\theta } $ is -

Question 5 :
In a triangle {tex} A B C {/tex} with fixed base {tex} B C , {/tex} the vertex {tex} A {/tex} moves such that {tex} \cos B + \cos C = 4 \sin ^ { 2 } ( A / 2 ) {/tex} If {tex} a , b , c {/tex} denote the lengths of the sides of the triangle opposite to the angles {tex} A , B {/tex} and {tex} C , {/tex} respectively, then

Question 6 :
If $\displaystyle \sin x+\sin y+\sin z+\sin w= -4$, then the value of $\displaystyle \sin ^{400}x+\sin ^{300}y +\sin ^{200}z+\sin ^{100}w $ is<br/>

Question 7 :
How many arrangements of the letters of the word $'BENGALI'$ can be made<br>i) If the vowels are never together<br>ii) If the vowels are to occupy only odd places

Question 8 :
A train is going from London to Cambridge stops at 12 intermediate stations. 75 persons enter the train during the journey with 75 different tickets of the same class. Number of different sets of tickets they may be holding is

Question 9 :
The number of different matrices that can be formed with elements 0,1,2 or 3, each matrix having 4 elements, is

Question 10 :
Two rays are drawn through a point $A$ at an angle of $30^{o}.$ A point $B$ is taken on one of them at distance $a$ from the point $A$. A perpendicular is drawn from the point $B$ to the other ray. Another perpendicular is drawn from its foot to $AB$, and so on then the length of the resulting infinite polygonal line is<br>

Question 11 :
The sum to $50$ terms of the series $1+2\left(\dfrac {1 1 }{ 50} \right) +3{ \left(\dfrac { 11 }{ 50} \right)}^{ 2 }+\dots $ is given by<br>

Question 12 :
The positive integer $n$ for which $2. { 2 }^{ 2 }+3. { 2 }^{ 3 }+4. { 2 }^{ 4 }+\cdots +n. { 2 }^{ n }={ 2 }^{ n+10 }$ is<br/>

Question 13 :
If one of the diagonals of a square is along the line $4x=2y$ and one of its vertices is $(3,0),$ then its side through this vertex nearer to the origin is given by the equation.

Question 14 :
Find the angle of inclination (in degrees) of the line passing through the points $(1,2)$ and $(2,3)$.

Question 15 :
The condition on $a$ and $b,$ such that the portion of the line $ax+by- 1= 0$, intercepted between the lines $ax+y = 0$ and $x+by=0$, subtends a right angle at the origin is

Question 16 :
<p>Two sides of a triangle are the lines (<em>a</em>+<em>b</em>)<em>x</em> + (<em>a</em>−<em>b</em>)<em>y</em> − 2ab = 0</p> <p>(<em>a</em>−<em>b</em>)<em>x</em> + (<em>a</em>+<em>b</em>)<em>y</em> − 2ab = 0. If the triangle is isosceles and the third side passes through point (<em>b</em> − <em>a</em>, <em>a</em> − <em>b</em>), then the equation of third side can be</p>

Question 17 :
If one of the diagonals of a square is along the line $x=2y$ and one of its vertices is $\left(3,0\right)$, then its sides through this vertex are given by the equations

Question 18 :
Let {tex} P ( a \cos \theta , b \sin \theta ) {/tex} and {tex} Q ( a \cos \phi , b \sin \phi ) {/tex} where {tex} \theta + \phi = \frac { \pi } { 2 } {/tex} be two points on the ellipse {tex} \frac { x ^ { 2 } } { a ^ { 2 } } + \frac { y ^ { 2 } } { b ^ { 2 } } = 1 {/tex} The locus of point of intersections of normals at {tex} P {/tex} and {tex} Q {/tex} is

Question 19 :
If two distinct chords, drawn from the point {tex} ( p , q ) {/tex} on the circle {tex} x ^ { 2 } + y ^ { 2 } = p x + q y ( \text { where } p q \neq 0 ) {/tex} are bisected by the {tex} x {/tex} -axis, then

Question 20 :
The normal {tex} y = m x - 2 a m - a m ^ { 3 } {/tex} to the parabola {tex} y ^ { 2 } = 4 a x {/tex} subtends a right angle at the vertex if