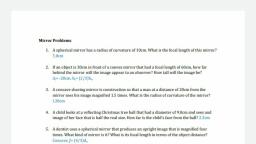
Question 1 :
<div>Classify the following function $f(x)$ defined in $R \rightarrow R$ as injective, surjective, both or none: <br/></div>$f(x) =(x^2\,+\,x\,+\,5)\,(x^2\,+\,x\,-\,3)$

Question 2 :
If $f(x)=\left[ x \right] +\left[ x+\cfrac { 1 }{ 3 } \right] +\left[ x+\cfrac { 2 }{ 3 } \right] $, then $(\left[ . \right] $ denotes the greatest integer function)

Question 3 :
Which one of the following is an elementary symmetric function of $\displaystyle x_{1},x_{2},x_{3},x_{4}$<br/>

Question 4 :
Let D be the union of $\displaystyle n\geq 1$ concentric circles in the plane. Suppose that the function $\displaystyle f: D\rightarrow D$ satisfies $\displaystyle d\left ( f\left ( A \right ), f\left ( B \right ) \right )\geq d\left ( A,B \right )$ for every A, B $\displaystyle \epsilon $ D (d(M, N) is the distance between the points M and N). Then for every A, B$\displaystyle \epsilon $ D

Question 5 :
Let $f:R\rightarrow R$ such that $\displaystyle f(x)=\frac{1}{1+x^{2}},x\in R$. Then $f$ is<br>

Question 6 :
If f : R $\rightarrow$ R, g : R $\rightarrow$ R and h : R $\rightarrow$ R is such that $f(x) = x^2, g(x) = tan x$ and $h(x) = log x$, then the value of [ho(gof)], if $x = \displaystyle \dfrac{\pi}{2}$ will be

Question 7 :
<div>Are the following sets of ordered pairs functions? If so, examine whether the mapping is surjective or injective :<br/></div>{(x, y): x is a person, y is the mother of x}

Question 10 :
If a $f(x)+bf\left( \cfrac { 1 }{ x } \right) =\dfrac{1}{x}-5,x\neq 0$ and $a\neq b$, then $f(2) $ is equal to