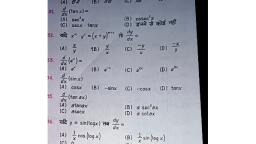Question 1 :
If the function $$\displaystyle f(x)=\begin{cases} 2x^{2}-3 & \text{ if } 0<x\leq 1 \\ x^{2}+bx-1 & \text{ if } 1<x<2 \end{cases}$$ is continuous at every point of its domain then the value of $$b$$ is 
Question 2 :
If $$f(x)=\displaystyle\frac{\log(1+ax)-log(1-bx)}{x}$$ for $$x\neq 0$$ and $$f(0)=k$$ and $$f(x)$$ is continuous at $$x=0$$, then $$k$$ is equal to:<br>
Question 3 :
If as continuous function 'f' satisfies the realation <br/>$$\int_{0}^{t}(f(x) \, - \, \sqrt{f^1(x)})dx \, = \, 0 \, and \, f(0) \, = \, {-1}$$<br/>the f(x) is equal to
Question 4 :
If $$f(x) = (1 + 2x)^{\frac{1}{x}}$$, for $$x \neq 0$$ is continuous at $$x = 0$$, then $$f(0) = $$_______.
Question 5 :
Function $$f(x) = \left\{\begin{matrix}(\log_{2}2x)^{\log_{x} 8};& x\neq 1\\(k - 1)^{3};& x = 1\end{matrix}\right.$$ is continuous at $$x = 1$$, then $$k =$$ _______.<br>
Question 6 :
If $$f\left( x \right) =\dfrac { 3sinx-sin\left( 3x \right) }{ { 2x }^{ 3 } } ,x\neq 0,f\left( 0 \right) =2,$$ at $$x=0,f$$ is
Question 7 :
The integer $$'n'$$ for which $$\mathop {\lim }\limits_{x \to 0} \dfrac{{\cos 2x - 1}}{{{x^n}}}$$ is a finite non-zero number is
Question 8 :
If $$f(x) = \begin{cases}\dfrac{x^2-(a+2)x+a}{x-2} & x\ne 2\\ 2 & x = 2 \end{cases}$$ is continuous at $$x = 2$$, then the value of $$a$$ is
Question 9 :
The function $$f\left( x \right)=\left[ x \right] ,$$  at $${ x }=5$$ is:<br/>
Question 10 :
If $$f(x)=\displaystyle \frac{\sin x}{x},x\neq 0$$ is to be continuous at $${x}=0$$ then $$\mathrm{f}({0})=$$<br/>
Question 11 :
Following function is continous at the point $$x=2$$ <br/>          $$f\left( x \right) = \left\{ \begin{array}{l}1 + x,\,\,\,\,when\,\,x < 2\\5 - x,\,\,\,\,when\,\,x \ge 2\end{array} \right.$$
Question 12 :
If $$ f\left( x \right) =\begin{cases} 1 & x<0 \\ { x }^{ 2 } & x\ge 0 \end{cases}$$ then at $$x=0$$
Question 13 :
The function $$f(x)=\dfrac{1-\sin x+\cos x}{1+\sin x+\cos x}$$ is not defined at $$x=\pi$$. The value of $$f(\pi)$$ so that $$f(x)$$ is continuous at $$x=\pi$$ is
Question 14 :
$$f(x)=\left\{\begin{matrix} 2x-1& if &x>2 \\ k & if &x=2 \\  x^{2}-1& if & x<2\end{matrix}\right.$$is continuous at $$x= 2$$ then $$k =$$
Question 15 :
<br/>The function $$f(x)=\begin{cases}(1+x)^{\frac{5}{x}}& for \ {x}\neq 0,\\ e^{5} & for \  {x}=0\end{cases}$$ is ........ at $${x}=0$$<br/>
Question 17 :
The functions $$f(x) = \left (\dfrac {\log_{e}(1 + ax) - \log_{e}(1 - bx)}{x}\right )$$ is undefined at $$x = 0$$. The value which should be assigned to $$f$$ at $$x = 0$$ so that it is continuous at $$x = 0$$ is
Question 18 :
If the function $$f(x)$$ defined as$$\displaystyle f\left( x \right) =\begin{cases} \begin{matrix} { \left( \sin { x } +\cos { x }  \right)  }^{ \csc { x }  }, & -\frac { \pi  }{ 2 } <x<0 \end{matrix} \\ \begin{matrix} a, & x=0 \end{matrix} \\ \begin{matrix} \frac { { e }^{ 1/x }+{ e }^{ 2/x }+{ e }^{ 3/x } }{ a{ e }^{ -2+1/x }+b{ e }^{ -1+3/x } } , & 0<x<\frac { \pi  }{ 2 }  \end{matrix} \end{cases}$$ is continuous at $$x=0$$, then
Question 19 :
Let $$f\left( x \right)  = \dfrac { 1-\tan { x }  }{ 4x-\pi  } , x \neq  \pi /4and x \in \left[ 0, \pi /2 \right]  = \lambda , x= \pi /4$$ if $$f\left( x \right)$$ is continuous in $$\left( 0, \pi /2 \right) , then\lambda $$ then
Question 20 :
If $$f\left( x \right) =\left\{ \begin{matrix} x& \text{if}\,\, x\,\, \text{is rational} \\ -x& \text{if}\,\, x\,\, \text{is irratonal} \end{matrix} \right. $$, then $$f(x)$$ is:
Question 21 :
The function $$f\left( x \right)=\sin ^{ -1 }{ \left( \cos { x }  \right)  } $$ is
Question 22 :
Let $$f\left( x \right) =\begin{cases} { x }^{ 3 }-{ x }^{ 2 }+10x-5\quad ,x\le 1 \\ -2x+\log _{ 2 }{ \left( { b }^{ 2 }-2 \right) ,x>1 }  \end{cases}$$ the set of values of $$b$$ for which $$f\left( x \right) $$ has greatest <br/>value at $$x=1$$ is given by:
Question 23 :
If $$f(x) =\begin{cases} \dfrac{\sin(p+1)x + \sin x}{x}& , &x < 0\\\quad \quad \quad q&,& x = 0\\ \dfrac{\sqrt{x^2 + x}- \sqrt{x}}{x^{3/2}}&,& x > 0\end{cases}$$ is continuous at $$x = 0$$ the $$(p, q)$$ is
Question 25 :
If $$f\left ( x \right )=\begin{cases} \displaystyle \frac{1}{5}\left ( 2x^{2}+3 \right ) & -\infty < x\leq 1 \\6-5x & 1< x< 3 \\x-3 & 3\leq x< \infty \\<br>\end{cases} $$
Question 26 :
<br>lf $$f(x)=<br>\left\{\begin{matrix}(1+|\sin x|)^{\displaystyle \frac{a}{|\sin x|}}&-\displaystyle \frac{\pi}{6}<x<0\\b&x=0 \\e^{\displaystyle \frac{\tan 2x}{\tan 3x}} &0<x<\displaystyle \frac{\pi}{6}\end{matrix}\right.$$ is<br><br>continuous at $$\mathrm{x}=0$$ then<br>
Question 27 :
If $$f(x) = \left\{\begin{matrix}\dfrac {1 - \cos x}{x},& x\neq 0\\ k,& x = 0\end{matrix}\right.$$ is continuous at $$x = 0$$, then the value of $$k$$ is<br>
Question 28 :
The function  $$\displaystyle f(x)=\begin{cases}\displaystyle \frac{x^{2}}{a} & 0\leq x< 1 \\ a & 1\leq x< \sqrt{2} \\ (2b^{2}-4b)/x^{2} & \sqrt{2}\leq x< \infty  \end{cases}$$ is continuous for $$0\leq x< \infty $$, then the most suitable values of $$a$$ and $$b$$ are