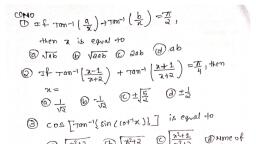Question 1 :
Solve:$$\displaystyle \sin { \left( { \tan }^{ -1 }x \right) } ,\left| x \right| <1$$ is equal to

Question 3 :
Calculate the value of $$\displaystyle \sin^{-1} \cos \left ( \sin^{-1} x\right ) + \cos^{-1} \sin \left ( \cos^{-1} x \right ) $$. where $$\displaystyle\left | x \right | \leq 1$$

Question 4 :
The value of $$\cos^{-1} (\cos 12) - \sin^{-1} (\sin 12)$$ is 

Question 6 :
Solve $$\cos { \left[ \tan ^{ -1 }{ \left[ \sin { \left( \cot ^{ -1 }{ x }  \right)  }  \right]  }  \right]  } $$

Question 8 :
Simplify $${\cot ^{ - 1}}\dfrac{1}{{\sqrt {{x^2} - 1} }}$$ for $$x <  - 1$$

Question 9 :
$$\quad \sin ^{ -1 }{ x } +\sin ^{ -1 }{ \cfrac { 1 }{ x } } +\cos ^{ -1 }{ x } +\cos ^{ -1 }{ \cfrac { 1 }{ x } = } $$

Question 11 :
If $$\cos ^{ -1 }{ \left( \cfrac { 1 }{ x } \right) } =\theta $$ then $$\tan { \theta } =$$

Question 12 :
$$\tan ^{ -1 }{ x } +2\cot ^{ -1 }{ x } =\cfrac { 2\pi }{ 3 } $$, then the value of $$x$$ is-

Question 13 :
The value of $$\sin ^{ -1 }{ \left[ \cos { \left\{ \cos ^{ -1 }{ \left( \cos { x } \right) } +\sin ^{ -1 }{ \left( \sin { x } \right) } \right\} } \right] } $$, where $$x\in \left( \cfrac { \pi }{ 2 } ,\pi \right) $$ is equal to

Question 14 :
If $$x=\sin ^{ -1 }{ K } $$, $$y=\cos ^{ -1 }{ K } $$, $$-1\le K\le 1$$, then the correct relationship is-

Question 15 :
If $$\displaystyle \cos \left ( 2\sin^{-1}x \right )=\frac{1}{9}$$,&#160; the value of x which satify equation is $$\pm \dfrac{a}{b}$$. Find the value of $$a+b$$<br/>

Question 16 :
Find the value of $$x$$ if $$\sin (arc \sin x) = \dfrac {\sqrt {2}}{4}$$

Question 17 :
The value of $$ \tan^{-1}\left (\displaystyle\frac{1}{2}\tan 2A \right )+\tan^{-1}\left ( \cot A\right )+\tan^{-1}\left ( \cot ^{3}A\right ) $$, for $$ 0&lt; A&lt; \pi /4 $$, is :<br>

Question 18 :
Assertion: If $$\alpha, \beta$$ are the roots of the equation $$18(tan^{-1} x)^2 - 9\pi tan^{-1} x + \pi^2 = 0$$ then $$\alpha + \beta = \dfrac {4}{\sqrt{3}}$$. Reason: $$sec^2 \left(cos^{-1} \left(\dfrac 14\right)\right) + cosec^2 \left(sin^{-1} \left(\dfrac 15\right)\right) = 41$$

Question 19 :
The value of $$\sin ^{ -1 }{ \left( \cos { \cfrac { 53\pi }{ 5 } } \right) } $$ is

Question 20 :
If $$\dfrac {(x + 1)^{2}}{x^{3} + x} = \dfrac {A}{x} + \dfrac {Bx + C}{x^{2} + 1}$$, then $$\csc^{-1}\left (\dfrac {1}{A}\right ) + \cot^{-1}\left (\dfrac {1}{B}\right ) + \sec^{-1}C =$$ ____

Question 22 :
What is $$\tan ^{ -1 }{ \left( \dfrac { 1 }{ 2 } \right) } +\tan ^{ -1 }{ \left( \dfrac { 1 }{ 3 } \right) } $$ equal to?

Question 23 :
If $$\sin ^{ -1 }{ \left( \cfrac { x }{ 13 } \right) } +co\sec ^{ -1 }{ \left( \cfrac { 13 }{ 12 } \right) } =\cfrac { \pi }{ 2 } $$, then the value if $$x$$ is

Question 24 :
What is $$\sin { \left[ \sin ^{ -1 }{ \left( \cfrac { 3 }{ 5 } \right) } +\sin ^{ -1 }{ \left( \cfrac { 4 }{ 5 } \right) } \right] } $$ equal to?

Question 25 :
$$ \sin \left( 2 \sin^{-1} \sqrt{\dfrac{63}{65}} \right) $$<br/>is equal to :

Question 26 :
If two angles of a triangle are $$\tan ^{ -1 }{ (2) } $$ and $$\tan ^{ -1 }{ (3) } $$, then the third angle is

Question 27 :
The number of solutions for the equation $$2\sin ^{ -1 }{ \sqrt { { x }^{ 2 }-x+1 } &#160;} +\cos ^{ -1 }{ \sqrt { { x }^{ 2 }-x } &#160;} =\dfrac { 3\pi }{ 2 } $$ is

Question 28 :
Consider the following :<br>1. $${\sin}^{-1}\dfrac{4}{5}+{\sin}^{-1}\dfrac{3}{5}=\dfrac{\pi}{2}$$<br>2. $${\tan}^{-1}\sqrt{3}+{\tan}^{-1}1=-{\tan}^{-1}(2+\sqrt{3})$$<br>Which of the above is/are correct?

Question 29 :
The value of $$\tan { \left[ \dfrac { 1 }{ 2 } \cos ^{ -1 }{ \left( \dfrac { 2 }{ 3 } \right) } \right] } $$ is

Question 30 :
The value of $$ \cos \left( \sin^{-1} \left( \dfrac {2}{3} \right) \right) $$ is equal to :

Question 34 :
Let $$\displaystyle f:A\rightarrow B$$ be a function defined by $$\displaystyle y=f(x)$$ where f is a bijective function, means f is injective (one-one) as well as surjective (onto), then there exist a unique mapping $$\displaystyle g:B\rightarrow A$$ such that $$\displaystyle f(x)=y$$ if and only if $$\displaystyle g(y)=x\forall x \epsilon A,y \epsilon B $$ Then function g is said to be inverse of f and vice versa so we write $$\displaystyle g=f^{-1}:B\rightarrow A[\left \{ f(x),x \right \}:\left \{ x,f(x) \right \}\epsilon f^{-1}] $$when branch of an inverse function is not given (define) then we consider its principal value branch.<br/><br/>If $$\displaystyle -1&lt;x&lt;0$$,then $$\displaystyle \tan^{-1}x $$ equals?<br/>

Question 35 :
The value of $$a$$ for which $$\displaystyle ax^{2}+sin^{-1}(x^{2}-2x+2)+cos^{-1}(x^{2}-2x+2)=0$$ has areal solution is

Question 36 :
If $$3\cos ^{ -1 }{ x } +\sin ^{ -1 }{ x } =\pi $$, then $$x=.....$$

Question 37 :
If $$a&lt;\cfrac { 1 }{ 32 } $$, then the number of solutions of $${ \left( \sin ^{ -1 }{ x } \right) }^{ 3 }+{ \left( \cos ^{ -1 }{ x } \right) }^{ 3 }=a{ \pi }^{ 3 }$$, is<br>

Question 38 :
$$\displaystyle&#160;\sum _{ k=1 }^{ k=n }{ \tan ^{ -1 }{ \frac { 2k }{ 2+{ k }^{ 2 }+{ k }^{ 4 } }&#160; }&#160; } =\tan ^{ -1 }{ \left( \dfrac { 6 }{ 7 }&#160; \right)&#160; } $$, then the value of '$$n$$' is equal to

Question 39 :
$$\tan { ^{ -1 }\left( 3/5 \right) } +\tan { ^{ -1 }\left( 1/4 \right) } =$$

Question 40 :
The value of $$sin^{-1} x + cos^{-1} x (|x| \geq 1)$$ is