Test Details

Relations and Functions,Linear Programming

Dec 01, 8:00 AM

90 minutes

Dec 01, 9:30 AM

54.0 marks

MCQ

26 questions

AVAAN Academy

Ashish Khare Sir instills Academic Excellence in Students of various grades. An accomplished guru with an illustrious career, shaping dreams of numerous students and parents, spanning decades. Having held senior positions in various institutes earlier and has been instrumental in their growth. Equipped with a degree in Science who went on to do his Masters in Economics With 21+Yrs of Mentoring Experience for IIT JEE and Various Olympiads, he has mentored 1000s of JEE Qualifiers and Admits.

Class Details

Mathematics

Class XII OLD

Mathematics

Class XII Mathematics will be taught, keeping in mind the IIT JEE Main and IIT JEE Advanced syllabus. Once a topic is thoroughly done then the Advanced Level Problems will be dealt with. All classes will be taught by Ashish Khare Sir Emphasis on Think & Act will be the key, instead of rote lectures. Students are expected to make notes simultaneously during the lectures.

More from AVAAN Academy

(20)

Lecture

Lecture 2022-01-10

class-12th

Mathematics

0 Likes

43 Views

AVAAN Academy

Jan 10, 2022

Lecture

Lecture 2022-01-06

class-12th

Mathematics

0 Likes

27 Views

AVAAN Academy

Jan 06, 2022

Lecture

Lecture 2022-01-03

class-12th

Mathematics

0 Likes

13 Views

AVAAN Academy

Jan 03, 2022

Lecture

Lecture 2022-01-02

class-12th

Mathematics

0 Likes

33 Views

AVAAN Academy

Jan 02, 2022

Lecture

Lecture 2021-12-27

class-12th

Mathematics

0 Likes

17 Views

AVAAN Academy

Dec 27, 2021

Lecture

Lecture 2021-12-25

class-12th

Mathematics

0 Likes

18 Views

AVAAN Academy

Dec 25, 2021

Lecture

Lecture 2021-12-22

class-12th

Mathematics

0 Likes

26 Views

AVAAN Academy

Dec 22, 2021

Lecture

Lecture 2021-12-20

class-12th

Mathematics

0 Likes

18 Views

AVAAN Academy

Dec 20, 2021

Test

Ready,Steady,Go, Our Living World and 3 other Topics

class-4th

Mathematics

0 Likes

21 Views

AVAAN Academy

Dec 01, 2021

Test

Human Body: The Digestive and Excretory Systems, Adaptations in Animals and 1 other Topics

class-4th

Mathematics

0 Likes

15 Views

AVAAN Academy

Dec 01, 2021

Test

Characteristics of a computer, Input and output devices and 1 other Topics

class-12th

Mathematics

0 Likes

16 Views

AVAAN Academy

Dec 01, 2021

Test

The Fundamental Unit of Life,Tissues

class-9th

Mathematics

0 Likes

25 Views

AVAAN Academy

Dec 01, 2021

Test

The French Revolution,Socialism in Europe and the Russian Revolution

class-9th

Mathematics

0 Likes

20 Views

AVAAN Academy

Dec 01, 2021

Test

Matter in Our Surroundings,Is Matter Around Us Pure

class-9th

Mathematics

0 Likes

27 Views

AVAAN Academy

Dec 01, 2021

Test

Motion,Force and Laws of Motion

class-9th

Mathematics

0 Likes

23 Views

AVAAN Academy

Dec 01, 2021

Test

Puzzle Test, Cryptography and 1 other Topics

olympiadjuniors

Mathematics

0 Likes

14 Views

AVAAN Academy

Nov 27, 2021

Test

Vectors and Three-Dimensional Geometry

class-12th

Mathematics

0 Likes

25 Views

AVAAN Academy

Nov 27, 2021

Test

Algebra,Coordinate Geometry

class-9th

Mathematics

0 Likes

28 Views

AVAAN Academy

Nov 27, 2021

Test

Sets, Relations and Functions

b-com

Mathematics

0 Likes

0 Views

AVAAN Academy

Nov 27, 2021

Test

Sets, Relations and Functions

b-com

Mathematics

0 Likes

0 Views

AVAAN Academy

Nov 27, 2021

Recommended Content

(20)

Test

Relations and Functions,Linear Programming

class-12th

Maths

0 Likes

14 Views

Md Zakir Hussain

Nov 28, 2021

Test

Relations and Functions,Linear Programming

class-12th

Maths

0 Likes

14 Views

Md Zakir Hussain

Nov 28, 2021

Test

Relations and Functions,Linear Programming

class-12th

Maths

0 Likes

12 Views

Md Zakir Hussain

Nov 28, 2021

Test

Linear Programming

class-12th

Mathematics

0 Likes

4 Views

Shefali Singha

Feb 20, 2022

Test

Linear Programming

class-12th

Mathematics

0 Likes

19 Views

Amritesh Singh

Nov 25, 2021

Homework

Linear Programming

class-12th

Mathematics

0 Likes

10 Views

xyz

Jan 20, 2022

Test

Linear Programming

class-12th

Mathematics

0 Likes

5 Views

Romey Saini

Feb 04, 2022

Test

Linear Programming

class-12th

Mathematics

0 Likes

4 Views

Shefali Singha

Jan 15, 2022

Test

Linear Programming

class-12th

Mathematics

0 Likes

5 Views

Shefali Singha

Feb 18, 2022

Test

Linear Programming

class-12th

Mathematics

0 Likes

4 Views

Shefali Singha

Feb 21, 2022

Test

Linear Programming

class-12th

Mathematics

0 Likes

26 Views

Abhilash Ranjan

Dec 04, 2021

Test

Linear Programming

class-12th

Mathematics

0 Likes

5 Views

Yash Bhatnagar

Mar 28, 2022

Homework

Linear Programming

class-12th

Mathematics

0 Likes

3 Views

xyz

Jan 20, 2022

Homework

Linear Programming

class-12th

Mathematics

0 Likes

6 Views

xyz

Jan 20, 2022

Test

Relations and Functions

class-12th

Mathematics

0 Likes

5 Views

Anand yadav

Apr 02, 2022

Test

Relations And Functions

class-12th

Mathematics

0 Likes

16 Views

Umashankar Gangwar

Nov 15, 2021

Test

Relations and Functions

class-12th

Mathematics

0 Likes

5 Views

Rajit Kumar Singh

Jun 09, 2022

Test

Relations And Functions

class-12th

Mathematics

0 Likes

19 Views

pradeep

Nov 05, 2021

Test

Relations and Functions

class-12th

Mathematics

0 Likes

11 Views

Akshay Soni

Dec 11, 2021

Test

Relations and Functions

class-12th

Mathematics

0 Likes

1 Views

swarna

Jan 11, 2022

Question Text

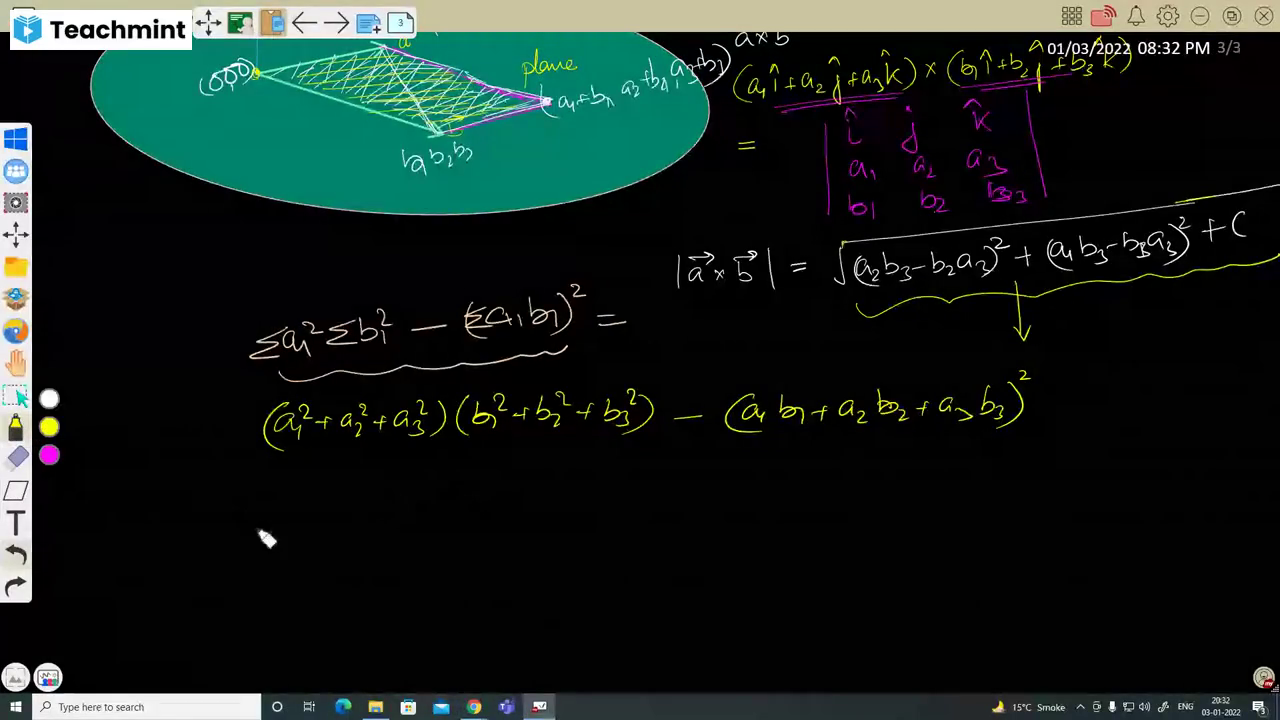
Question 2 :
The number of points in $\\ \left( -\infty ,\infty \right) $ for which ${ x }^{ 2 }-x\sin { x } -\cos { x } =0$, is

Question 3 :
In linear programming, lack of points for a solution set is said to

Question 4 :
What is the solution of $x\le 4,y\ge 0$ and $x\le -4,y\le 0$ ?

Question 6 :
Which of the following is a property of all linear programming problems?

Question 7 :
In graphical solutions of linear inequalities, solution can be divided into<ol></ol>

Question 8 :
If two constraints do not intersect in the positive quadrant of the graph, then

Question 9 :
If $a,b,c \in +R$ such that $\lambda abc$ is the minimum value of $a(b^2+c^2)+b(c^2+a^2)+c(a^2+b^2)$, then $\lambda=$

Question 10 :
In transportation models designed in linear programming, points of demand is classified as

Question 11 :
If $x+y \leq 2, x\leq 0, y\leq 0$ the point at which maximum value of $3x+2y$ attained will be.

Question 12 :
Find the output of the program given below if$ x = 48$ and $y = 60$ 10  $ READ x, y$ 20  $Let x = x/3$ 30  $ Let y = x + y + 8$ 40  $ z = \dfrac y4$ 50  $PRINT z$ 60  $End$

Question 13 :
Conclude from the following: $n^2 > 10$, and n is a positive integer.A: $n^3$B: $50$

Question 14 :
Consider the following two binary relations on the set $A = \left \{a, b, c\right \} : R_{1} = \left \{(c, a), (b, b), (a, c), (c, c), (b, c), (a, a)\right \}$ and $R_{2} = \left \{(a, b), (b, a), (c, c), (c, a), (a, a), (b, b), (a, c)\right \}$ Then

Question 15 :
If $f: A \rightarrow B$is a bijective function and if n(A) = 5, then n(B) is equal to

Question 17 :
Let $R$ be the relation over the set of all straight lines in a plane such that ${l}_{1}$ $R$ ${l}_{2}\Leftrightarrow {l}_{1}\bot {l}_{2}$. Then, $R$ is

Question 18 :
Let $f(x,y)=xy^{2}$ if $x$ and $y$ satisfy $x^{2}+y^{2}=9$ then the minimum value of $f(x,y)$ is

Question 19 :
If the function $f:R\rightarrow A$ given by $f(x)=\cfrac { { x }^{ 2 } }{ { x }^{ 2 }+1 } $ is surjection, then $A=$

Question 21 :
Let $S$ be a relation on $\mathbb{R}^{+}$ defined by $xSy\Leftrightarrow { x }^{ 2 }-{ y }^{ 2 }=2\left( y-x \right)$, then $S$ is

Question 22 :
The number of one-one functions that can be defined from $A=\{4,8,12,16\}$ to $B$ is $5040,$ then $n(B)=$

Question 23 :
The number of possible surjection from $A=\{1,2,3,...n\}$ to $B = \{1,2\}$ (where $n \geq 2)$ is $62$,then $n=$

Question 24 :
If $f:R\rightarrow \left [\dfrac {\pi}{6}, \dfrac {\pi}{2}\right ), f(x)=\sin^{-1}\left (\dfrac {x^2-a}{x^2+1}\right )$ is a onto function, then set of values of $a$ is

Question 25 :
Let $f:{x, y, z}\rightarrow (a, b, c)$ be a one-one function. It is known that only one of the following statements is true:(i) $f(x)\neq b$ (ii)$f(y)=b$ (iii)$f(z)\neq  a$

Question 26 :
In the following functions defined from $[-1, 1]$ to $[-1, 1]$, then functions which are not bijective are

More from AVAAN Academy

Recommended Content

Learn from Anywhere on Any Device