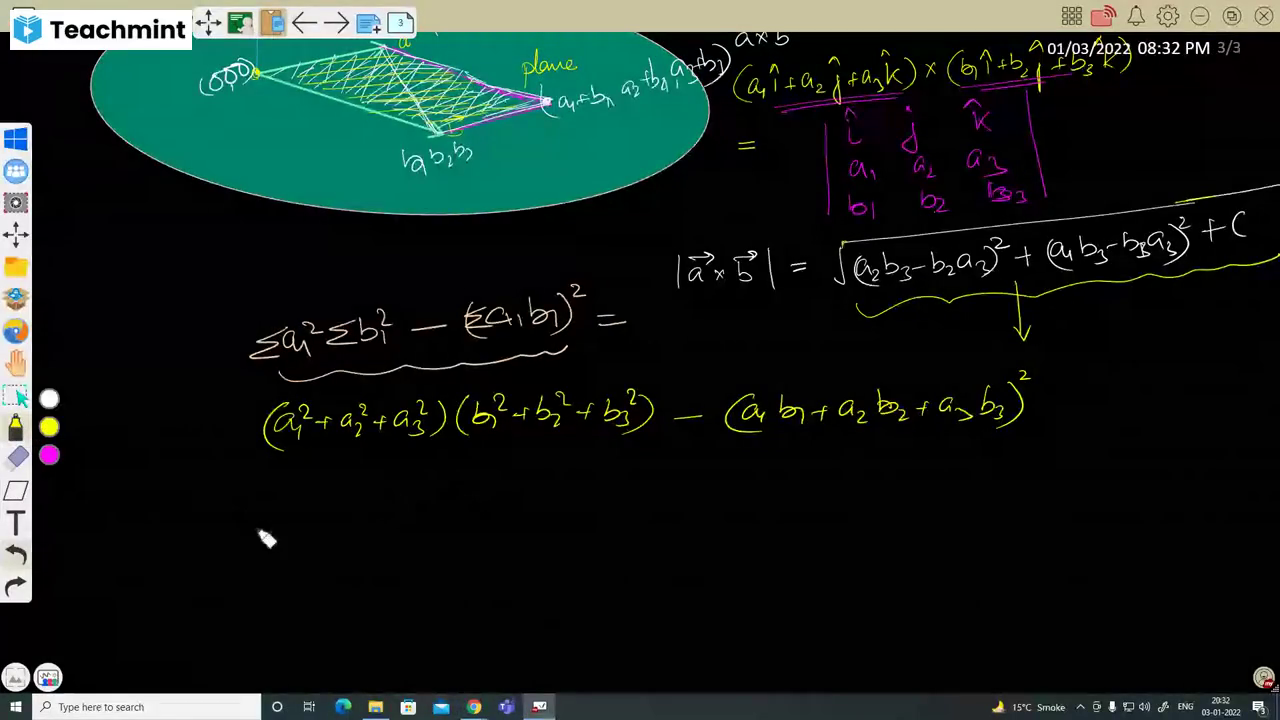
Question 1 :
A line with positive direction cosines passes through the point {tex} P ( 2 , - 1,2 ) {/tex} and makes equal angles with the coordinate axes. The line meets the plane {tex} 2 x + y + z = 9 {/tex} at point {tex} Q . {/tex} The length of the line segment {tex} P Q {/tex} equals

Question 2 :
A plane {tex} 2 x + 3 y + 5 z = 1 {/tex} has a point {tex} P {/tex} which is at minimum distance from line joining {tex} A ( 1,0 , - 3 ) {/tex} and {tex} B ( 1 , - 5,7 ) {/tex} then distance {tex} A P {/tex} is equal to

Question 3 :
Let {tex} a = 2 i + j - 2 k {/tex} and {tex} b = i + j . {/tex} If {tex} c {/tex} is a vector such that {tex} a {/tex}. {tex} c = | \mathbf { c } | , | c - a | = 2 \sqrt { 2 } {/tex} and the angle between {tex} ( a \times b ) {/tex} and {tex} c {/tex} is {tex} 30 ^ { \circ } , {/tex} then {tex} | ( a \times b ) \times c | = {/tex}

Question 4 :
Equation of the plane containing the straight line {tex} \frac { x } { 2 } = \frac { y } { 3 } = \frac { z } { 4 } {/tex} and perpendicular to the plane containing the straight lines {tex} \frac { x } { 3 } = \frac { y } { 4 } = \frac { z } { 2 } {/tex} and {tex} \frac { x } { 4 } = \frac { y } { 2 } = \frac { z } { 3 } {/tex} is

Question 5 :
If {tex}\vec{a}{/tex}and {tex}\vec{b}{/tex}are orthogonal unit vectors, then for a vector {tex}\vec{r}{/tex} non-coplanar with {tex}\vec{a}{/tex}and {tex}\vec{b}{/tex}, vector {tex}\vec{r}{/tex} × {tex}\vec{a}{/tex} is equal to

Question 6 :
Let two non-collinear unit vectors {tex} \hat { a } {/tex} and {tex} \hat { b } {/tex} form an acute angle. A point {tex} P {/tex} moves so that any time {tex} t {/tex} the position vector {tex} \left.\overrightarrow{ OP}\text { (where } O \text { is the origin } \right) {/tex} is given by {tex} \hat { a } {/tex} cos t {tex} + \hat { b } {/tex} sint. When {tex} P {/tex} is farthest from origin {tex} O , {/tex} let {tex} M {/tex} be the length of {tex} \overrightarrow{OP} {/tex} and {tex} \hat { u } {/tex} be the unit vector along

Question 7 :
Let {tex} \hat { a } , \hat b , \hat { c } {/tex} be unit vectors such that {tex} \hat { a } \times \hat { b } = \hat { c } {/tex} and {tex} \hat { a } \cdot \hat { b } = 0 {/tex}. Also, {tex} \vec { x } {/tex} is any vectors such that {tex} [\vec x\ \hat { b }\ \hat { c } ] = 3 , [\vec x\ \hat { c }\ \hat { a } ] = 4 {/tex} and {tex} [ \vec { x }\ \hat { a }\ \hat { b } ] = 2 {/tex}. Then {tex} \vec { x } {/tex} is equal to

Question 8 :
If the lines<br>{tex} \frac { x - 1 } { 2 } = \frac { y + 1 } { 3 } = \frac { z - 1 } { 4 } {/tex} and {tex} \frac { x - 3 } { 1 } = \frac { y - k } { 2 } = \frac { z } { 1 } {/tex} intersect {tex} , {/tex} then<br>the value of {tex} k {/tex} is

Question 9 :
Let {tex} \vec { a } = \hat { i } + \hat { j } + \hat { k } , \vec { b } = \hat { i } - \hat { j } + \hat { k } {/tex} and {tex} \vec { c } = \hat { i } - \hat { j } - \hat { k } {/tex} be three vectors. A vector {tex} \vec { v } {/tex} in the plane of {tex} \vec { a } {/tex} and {tex} \vec { b } , {/tex} whose projection on {tex} \vec { c } {/tex} is {tex} \frac { 1 } { \sqrt { 3 } } , {/tex} is given by

Question 10 :
If <em>a</em>({tex}\vec{α}{/tex}×{tex}\vec{β}{/tex}) + <em>b</em>({tex}\vec{β}{/tex}×{tex}\vec{γ}{/tex}) + <em>c</em>({tex}\vec{γ}{/tex}×{tex}\vec{α}{/tex}) = 0 and at least one of <em>a</em>, <em>b</em> and <em>c</em> is non-zero, then vectors {tex}\vec{α}{/tex}, {tex}\vec{β}{/tex}and {tex}\vec{γ}{/tex}are

Question 11 :
If {tex} \vec { a } , \vec { b } , \vec { c } {/tex} and {tex} \vec { d } {/tex} are unit vectors such that {tex} ( \vec { a } \times \vec { b } ) \cdot ( \vec { c } \times \vec { d } ) = 1 {/tex} and {tex} \vec { a } \cdot \vec { c } = \frac { 1 } { 2 } , {/tex} then

Question 12 :
If {tex} \vec { a } , \vec { b } {/tex} and {tex} \vec { c } {/tex} are unit coplanar vectors, then the scalar triple product {tex} [ 2 \vec { a } - \vec { b } , 2 \vec { b } - \vec { c } , 2 \vec { c } - \vec { a } ] = {/tex}

Question 13 :
Let a plane passes through origin and is parallel to line {tex} \frac { x - 1 } { 2 } = \frac { y + 3 } { - 1 } = \frac { z + 1 } { - 2 } {/tex} such that the distance between plane and line is {tex} 5 / 3 , {/tex} then the equation of plane is

Question 14 :
If {tex} \vec { x } {/tex} and {tex} \vec { y } {/tex} be unit vectors and {tex} | \vec{z} | = \frac { 2 } { \sqrt { 7 } } {/tex} such that {tex}\vec z + \vec z \times \vec { x } = \vec { y } {/tex}, then the angle {tex} \theta {/tex} between {tex} \vec { x } {/tex} and {tex} \vec { z } {/tex} is

Question 15 :
Let {tex} \vec { a } = \hat { i } - \hat { j } , \vec { b } = \hat { j } - \hat { k } , \vec { c } = \hat { k } - \hat { i } . {/tex} If {tex} \vec { d } {/tex} isa unit vector such that {tex} \vec { a } \vec { d } = 0 = [ \vec { b } \vec { c } \vec { d } ] , {/tex} then {tex} \vec { d } {/tex} equals

Question 16 :
For non-zero vectors {tex} \vec { a } , \vec { b } , \vec { c } , | ( \vec { a } \times \vec { b } ) \cdot \vec { c } | = | \vec { a } | | \vec { b } | | \vec { c } | {/tex} holds if and only if

Question 17 :
In {tex} R ^ { 3 } , {/tex} let {tex} L {/tex} be a straight line passing through the origin. Suppose that all the points on {tex} L {/tex} are at a constant distance from the two planes {tex} P _ { 1 }: x + 2 y - z + 1 = 0 {/tex} and {tex} P _ { 2 }: 2 x - y + z {/tex} {tex} - 1 = 0 . {/tex} Let {tex} M {/tex} be the locus of the feet of the perpendiculars drawn from the points on {tex} L {/tex} to the plane {tex} P _ { 1 } {/tex}. Which of the following points lie (s) on {tex} M {/tex} ?

Question 18 :
The volume of the tetrahedron, the equations of whose faces are {tex} a _ { i } x + b _ { i } y + c _ { i } z + d _ { i } = 0 ( i = 1,2,3,4 ) {/tex} is {tex} \left| \frac { \Delta ^ { 3 } } { 6 D _ { 1 } D _ { 2 } D _ { 3 } D _ { 4 } } \right| {/tex} where {tex} D _ { 1 } , D _ { 2 } , D _ { 3 } , {/tex} and {tex} D _ { 4 } {/tex} are cofactors of {tex} d _ { 1 } , d _ { 2 } , d _ { 3 } {/tex} and {tex} d _ { 4 } {/tex}<br>{tex} \operatorname { in } \Delta = \left| \begin{array} { l l l l } a _ { 1 } & b _ { 1 } & c _ { 1 } & d _ { 1 } \\ a _ { 2 } & b _ { 2 } & c _ { 2 } & d _ { 2 } \\ a _ { 3 } & b _ { 3 } & c _ { 3 } & d _ { 3 } \\ a _ { 4 } & b _ { 4 } & c _ { 4 } & d _ { 4 } \end{array} \right| {/tex}<br>The magnitude of the volume of the tetrahedron formed by the planes {tex} 2 x + 3 y + z = 6,2 x + 3 y = 0 , {/tex} {tex} 3 y + z = 0 {/tex} and {tex} 2 x + z = 0 {/tex} is

Question 19 :
If a non-zero vector {tex} \vec { a } {/tex} is parallel to the line of intersection of the plane {tex} P _ { 1 } {/tex} determined by {tex} \hat { i } + \hat { j } {/tex} and {tex} \hat { i } - 2 \hat { j } {/tex} and plane {tex} P _ { 2 } {/tex} determined by vector {tex} 2 \hat { i } + \hat { j } {/tex} and {tex} 3 \hat { i } + 2 \hat { k } {/tex}, then angle between {tex} \vec { a } {/tex} and vector {tex} \hat { i } - 2 \hat { j } + 2 \hat { k } {/tex} is

Question 20 :
In a triangle {tex} O A B , E {/tex} is the mid-point of {tex} O B {/tex} and {tex} D {/tex} is a point on {tex} A B {/tex} such that {tex} A D: D B = 2: 1 . {/tex} If {tex} O D {/tex} and {tex} A E {/tex} intersect at {tex} P {/tex}, then ratio of {tex} \frac { O P } { P D } {/tex} is equal to