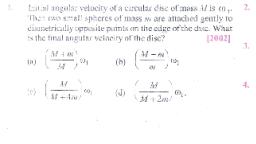Question 1 :
Coefficient of $x^{50}$ in the polynomial <br/>$\left(x+_{ }^{ 50 }{ { C }_{ 0 } }\right)\left(x+3._{ }^{ 50 }{ { C }_{ 1 } }\right)\left(x+5._{ }^{ 50 }{ { C }_{ 2 } }\right).....\left[x+(101)._{ }^{ 50 }{ { C }_{ 50 } }\right]$ is
Question 2 :
If the last term in the binomial expansion of <br>${ \left( { 2 }^{ 1/3 }-\cfrac { 1 }{ \sqrt { 2 } } \right) }^{ n }$ is ${ \left( \cfrac { 1 }{ { 3 }^{ 5/3 } } \right) }^{ \log _{ 3 }{ 8 } }$, then the 5th term from the beginning is<br>
Question 3 :
Find the coefficient of ${ x }^{ 50 }$ in the expression:<br>${ \left( 1+x \right) }^{ 1000 }+2x{ \left( 1+x \right) }^{ 999 }+3{ x }^{ 2 }{ \left( 1+x \right) }^{ 998 }+....+1001{ x }^{ 1000 }$<br>
Question 5 :
If there is a term containing $x^{2r}$ in $\left( x + \dfrac{1}{x^2} \right )^{n - 3}$, then
Question 7 :
Two rays are drawn through a point $A$ at an angle of $30^{o}.$ A point $B$ is taken on one of them at distance $a$ from the point $A$. A perpendicular is drawn from the point $B$ to the other ray. Another perpendicular is drawn from its foot to $AB$, and so on then the length of the resulting infinite polygonal line is<br>
Question 8 :
In a GP the ratio of the sum of the first {tex}11{/tex} terms to the sum of the last {tex}11{/tex} terms is {tex} \frac { 1 } { 8 } {/tex} and the ratio of the sum of all the terms without the first nine to the sum of all the terms without the last nine is {tex} 2 . {/tex} Then the number of terms of the GP is less than
Question 9 :
The sum to infinity of the series $1-3x+{ 5x }^{ 2 }-{ 7x }^{ 3 }+\cdots \infty$, when $|x|<1$, is<br>
Question 10 :
This sum to infinity of the series, $\displaystyle 1 + 2 \left ( 1 - \frac{1}{n} \right ) + 3 \left ( 1 - \frac{1}{n} \right )^2 + ...$ is<br>
Question 11 :
The sum to $50$ terms of the series $1+2\left(\dfrac {1 1 }{ 50} \right) +3{ \left(\dfrac { 11 }{ 50} \right)}^{ 2 }+\dots $ is given by<br>
Question 12 :
The sum to infinity of the series $1+\displaystyle \dfrac{2}{3}+\dfrac{6}{3^{2}}+\frac{10}{3^{3}}+\frac{14}{3^{4}}+$ ... is :<br>
Question 14 :
After striking the floor, a certain ball rebounds ${ (4/5) }^{ th }$ of height from which it has fallen. Then the total distance that it travels before coming to rest, if it is gently dropped from a height of 120 m is
Question 15 :
If $1\cdot3+3\cdot3^{2}+5\cdot3^{3}+7\cdot3^{4}+\cdots$ up to $n$ terms is equal to $3+\left ( n-1 \right )3^{t}$, then $t$=<br/>
Question 16 :
How many numbers can be formed by using all the digits $1,\space 2,\space 3,\space 4,\space 3,\space 2,\space 1$ so that the odd digits always occupy the odd places?
Question 17 :
Find the number of integers greater than $4000$ that can be formed by using the digits $3, 4, 5$ and $2$ if every digit can occur at most once in any number
Question 18 :
A coin tossed $100$ times. The no. of times head comes up is $54$.If the vowels always remain together
Question 19 :
Find the number of $5$-digit odd numbers that can be formed using the integers from $3$ to $9$ if no digit is to occur more than once in any number
Question 20 :
The number of $9$ lettered words that can be formed using all the letters of the word 'MEENANSHU' if alike letters are never adjacent, is $k(7!)$. Then $'k'$ lies in the interval:
Question 21 :
$7$ students of a hostel are to be allotted $7$ beds. Among them Praveen does not want a bed next to Nandu because Nandu snores.Then in how many ways can you allot the beds?
Question 22 :
How many necklaces of $10$ beads each can be made from $20$ beads of different colors?
Question 23 :
<div>Twelve persons are to be arranged around two round tables such that one table can accommodate seven persons and another five persons only. Answer the given question.<br/></div><div><br/></div>Number of ways in which these $12$ persons can be arranged is?
Question 24 :
A train is going from London to Cambridge stops at 12 intermediate stations. 75 persons enter the train during the journey with 75 different tickets of the same class. Number of different sets of tickets they may be holding is
Question 25 :
Let $ (a_1, a_2, a_3, . . . , a_{2011}) $ be a permutation (that is a rearrangement) of the numbers 1, 2, 3, . . . , 2011. Show that there exist two numbers $ j, k $ such that $ 1 \le j < k \le 2011 $ and $ |a_j - j| = |a_k - k|$