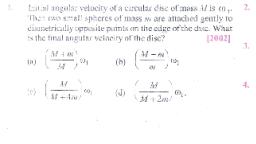Question 3 :
Two particles which are initially at rest, move towards each other under the action of their internal attraction. If their speeds are {tex} v {/tex} and {tex} 2 v {/tex} at any instant, then the speed of centre of mass of the system will be:

Question 4 :
In case of explosion of a bomb, which of the following changes?

Question 6 :
A particle is moving in a circular path. The correct statement out of the following is

Question 7 :
Two persons of masses {tex} 55 \mathrm { kg } {/tex} and {tex} 65 \mathrm { kg } {/tex} respectively, are at the opposite ends of a boat. The length of the boat is {tex}3.0 \mathrm m{/tex} and weighs {tex}100 \mathrm {kg}{/tex} . The {tex}55 \mathrm {kg}{/tex} man walks up to the {tex}65 \mathrm {kg}{/tex} man and sits with him. If the boat is in still water the centre of mass of the system shifts by :

Question 8 :
The moment of inertia of a body does not depend upon

Question 9 :
A disc is rotating with an angular speed of <img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/NEET/5e97fef1cf5ae23387f28f88"> . If a child sits on it, which of the following is conserved

Question 10 :
One circular ring and one circular disc, both are having the same mass and radius. The ratio of their moments of inertia about the axes passing through their centres and perpendicular to their planes, will be

Question 11 :
A solid cylinder of mass {tex} \mathrm { m } \ \& {/tex} radius {tex} \mathrm { R } {/tex} rolls down inclined plane without slipping. The speed of its {tex} \mathrm { C } . \mathrm { M } {/tex}. when it reaches the bottom is<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/NEET/5e0f0c6cde596850506e33bd"><br>

Question 12 :
A rod of mass {tex} m {/tex} and length {tex} l {/tex} is bent in to shape of {tex} L . {/tex} Its moment of inertia about the axis shown in figure<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/NEET/5e0f0e74ed6e36502132f394"><br>

Question 13 :
Two discs of same thickness but of different radii are made of two different materials such that their masses are same. The densities of the materials are in the ratio of {tex} 1 : 3 . {/tex} The moments of inertia of these discs about the respective axes passing through their centres and perpendicular to their planes will be in the ratio of<br>

Question 14 :
The moment of inertia of a body about a given axis is {tex} 1.2 \mathrm { kg } \mathrm { m } ^ { 2 } {/tex}. Initially, the body is at rest. In order to produce a rotational kinetic energy of {tex}1500{/tex} joule, an angular acceleration of {tex}25 \mathrm {radian/sec}^2{/tex} must be applied about that axis for a duration of

Question 15 :
The moment of inertia of a uniform circular disc (figure) is maximum about an axis perpendicular to the disc and passing through<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/NEET/5e0f0d67ed6e36502132f343"><br>

Question 16 :
One solid sphere {tex} A {/tex} and another hollow sphere {tex} B {/tex} are of same mass and same outer radii, Their moments of inertia about their diameters are respectively {tex} I _ { A } {/tex} and {tex} I _ { B } {/tex}, such that

Question 17 :
A metal sheet {tex} 14 \mathrm { cm } \times 2 \mathrm { cm } {/tex} of uniform thickness is cut into two pieces of width {tex} 2 \mathrm { cm } . {/tex} The two pieces are joined and laid along {tex} X Y {/tex} plane as shown. The centre of mass has the coordinates<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/NEET/5e0f0cb2ed6e36502132f2bd"><br>

Question 18 :
From a uniform wire, two circular loops are made (i) {tex} \mathrm { P } {/tex} of radius {tex} \mathrm { r } {/tex} and (ii) {tex} \mathrm { Q } {/tex} of radius {tex} \mathrm { nr } {/tex}. If the moment of inertia of {tex} \mathrm { Q } {/tex} about an axis passing through its centre and perpendicular to its plane is 8 times that of {tex} \mathrm { P } {/tex} about a similar axis, the value of {tex} \mathrm { n } {/tex} is (diameter of the wire is very much smaller than {tex} \mathrm { r } {/tex} or {tex} \mathrm { nr } {/tex} )<br>

Question 19 :
From a solid sphere of mass {tex} \mathrm { M } {/tex} and radius {tex} \mathrm { R } , {/tex} a cube of maximum possible volume is cut. Moment of inertia of cube<br>about an axis passing through its center and perpendicular to one of its faces is :<br>

Question 20 :
A bullet of mass {tex} 10 \mathrm { g } {/tex} and speed {tex} 500 \mathrm { m } / \mathrm { s } {/tex} is fired into a door and gets embedded exactly at the centre of the door. The door is {tex} 1.0 \mathrm { m } {/tex} wide and weighs {tex} 12 \mathrm { kg } {/tex}. It is hinged at one end and rotates about a vertical axis practically without friction. The angular speed of the door just after the bullet embeds into it will be:

Question 21 :
The moment of inertia of a uniform circular disc of radius 'R' and mass 'M' about an axis passing from the edge of the disc and normal to the disc is

Question 22 :
In a bicycle, the radius of rear wheel is twice the radius of front wheel. It {tex} r _ { f } {/tex} and {tex} r {/tex} are the radii and {tex} v _ { f } {/tex} and {tex} v _ { r } {/tex} are the speeds of topmost points of wheels then

Question 23 :
The free end of a thread wound on a bobbin is passed round a nail A hammered into the wall. The thread is pulled at a constant velocity. Assuming pure rolling of bobbin, find the velocity {tex} v _ { 0 } {/tex} of the centre of the bobbin at the instant when the thread forms an angle {tex} \alpha {/tex} with the vertical.

Question 24 :
Four point masses, each of value <b>m</b> ,are placed at the corners of a square <b> ABCD </b> of side {tex} \ell {/tex} . The moment of inertia of this system about an axis passing through <b>A</b> and parallel to <b>BD </b> is

Question 25 :
If {tex} \overrightarrow { \mathrm { F } } {/tex} is the force acting on a particle having position vector {tex} \overrightarrow { \mathrm { r } } {/tex} and {tex} \vec { \tau } {/tex} be the torque of this force about the origin, then: