Question 1 :
A ball is thrown vertically upward, the acceleration due to gravity:

Question 2 :
The radius of earth is about 6400 km and that ofmars is 3200 km. The mass of the earth is 10 times the mass of mars. An object weight 200 N on the surface of earth. Its weight on the surface of mars will be.

Question 3 :
Assertion: If earth suddenly stops rotating about its axis, then the value of acceleration due to gravity will become same at all the places. Reason: The value of acceleration due to gravity is independent of rotation of earth.

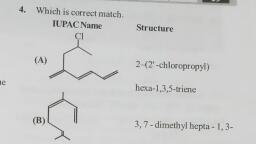
Question 6 :
Which of the following physical quantities has neither dimensions nor unit?

Question 9 :
The thrust developed by a rocket-motor is given by {tex} \mathrm { F } = \mathrm { mv } + \mathrm { A } \left( \mathrm { P } _ { 1 } - \mathrm { P } _ { 2 } \right) {/tex} where {tex} \mathrm { m } {/tex} is the mass of the gas ejected per unit time, {tex}\mathrm v{/tex} is velocity of the gas, {tex} \mathrm { A } {/tex} is area of cross-section of the nozzle, {tex} \mathrm { P } _ { 1 } {/tex} and {tex} \mathrm { P } _ { 2 } {/tex} are the pressures of the exhaust gas and surrounding atmosphere. The formula is dimensionally

Question 10 :
The resistance {tex} R {/tex} of a wire is given by the relation {tex} R = \frac { \rho \ell } { \pi r ^ { 2 } } . {/tex} Percentage error in the measurement of {tex} \rho , \ell {/tex} and {tex} r {/tex} is {tex} 1 \% , 2 \% {/tex} and {tex} 3 \% {/tex} respectively. Then the percentage error in the measurement of {tex} R {/tex} is

Question 12 :
{tex} \mathrm { E } , \mathrm { m } , \mathrm { J } {/tex} and {tex} \mathrm { G } {/tex} denote energy, mass, angular momentum and gravitational constant respectively, then the unit of {tex} \frac { \mathrm { E } \mathrm { J } ^ { 2 } } { \mathrm { m } ^ { 5 } \mathrm { G } ^ { 2 } } {/tex} is

Question 14 :
If {tex} \mathrm { v } = \frac { \mathrm { a } } { \mathrm { t } } + \mathrm { bt } ^ { 3 } {/tex} where {tex} \mathrm { v } = {/tex} velocity and {tex} \mathrm { t } {/tex} is time The dimensional formula of {tex} \mathrm { a } {/tex} and {tex} \mathrm { b} {/tex} are

Question 15 :
Two masses {tex} \mathrm { M } _ { \mathrm { A } } {/tex} and {tex} \mathrm { M } _ { \mathrm { B } } \left( \mathrm { M } _ { \mathrm { A } } < \mathrm { M } _ { \mathrm { B } } \right) {/tex} are weighed using same weighing machine. Absolute error and relative error in two measurement are (Assume only systematic errors are nvolved)

Question 16 :
An experiment is performed to obtain the value of acceleration due to gravity g by using a simple pendulum of length L. In this experiment time for 100 oscillations is measured by using a watch of 1 second least count and the value is 90.0 seconds. The length L is measured by using a meter scale of least count 1 mm and the value is 20.0 cm The error in the determination of g would be:

Question 17 :
The momentum of an electron in an orbit is {tex} h / \lambda {/tex} where {tex} h {/tex} is a constant and {tex} \lambda {/tex} is wavelength associated with it. The nuclear magneton of electron of charge {tex} e {/tex} and mass {tex} m _ { e } {/tex} is given as {tex} \mu _ { n } {/tex} {tex} = \frac { e h } { 3672 \pi m _ { e } } . {/tex} The dimensions of {tex} \mu _ { n } {/tex} are {tex} ( A \rightarrow \text { current } ) {/tex}<br>

Question 18 :
The refractive index of water measured by the relation {tex} \mu = \frac { \text { real depth } } { \text { apparent } } {/tex} is found to have values of 1.34, 1.38, 1.32 and 1.36, the mean value of refractive index with perfentage error is

Question 19 :
{tex} \mathrm { E } , \mathrm { m } , \mathrm { J } {/tex} and {tex}\mathrm G{/tex} denote energy, mass, angular momentum and gravitational constant respectively, then the unit of {tex} \frac { \mathrm { EJ } ^ { 2 } } { \mathrm { m } ^ { 5 } \mathrm { G } ^ { 2 } } {/tex} is

Question 21 :
In uniform circular motion, the velocity vector and acceleration vector are

Question 22 :
A body of mass <img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/NEET/5e97fed8cf5ae23387f28f3e">  moves in a circular path with uniform angular velocity. The motion of the body has constant

Question 23 :
A mass of 100 g is tied to one end of string 2 m long. The body is revolving in a horizontal circle making a maximum of 200 revolutions/min. The other end of the string is fixed at the centre of the circle of revolution. The maximum tension that the string can bear is approximately

Question 25 :
Which one of the following statements is not correct in a uniform circular motion

Question 26 :
The force required to keep a body in uniform circular motion is

Question 27 :
A body of mass 0.4 kg is whirled in a vertical circle making 2rev/s. If the radius of the circle is 2m, then tension in the string when the body is at the top of the circle is

Question 28 :
In case of uniform circular motion which of the following physical quantity do not remain constant

Question 29 :
In an atom for the electron to revolve around the nucleus, the necessary centripetal force is obtained from the following force exerted by the nucleus on the electron

Question 30 :
A body is tied to one end of the string and whirled in a vertical circle, the physical quantity which remains constant is

Question 31 :
A body is projected from the ground with a velocity {tex} 50 \mathrm { m } / \mathrm { s } {/tex} at an angle of {tex} 30 ^ { \circ } . {/tex} It crosses a wall after {tex}3 {/tex}sec. How far beyond the wall the stone will strike the ground? [take {tex} \left. \mathrm { g } = 10 \mathrm { m } / \mathrm { s } ^ { 2 } \right] {/tex}

Question 32 :
The range of a projectile is {tex} R {/tex} when the angle of projection is {tex} 40 ^ { \circ } . {/tex} For the same velocity of projection and range, the other possible angle of projection is

Question 33 :
A boat, which has a speed of {tex} 5 \mathrm { km } / \mathrm { h } {/tex} in still water, crosses a river of width {tex} 0.5 \mathrm { km } {/tex} along the shortest possible path. If the speed of the river is {tex} 4 \mathrm { km } / \mathrm { h } {/tex} then the time taken in minutes is

Question 34 :
A boat takes {tex}2 {/tex} hours to travel {tex} 8 \mathrm { km } {/tex} and back in still water. If the velocity of the water is {tex} 4 \mathrm { km } / \mathrm { h } {/tex}, then the time taken for going upstream of {tex} 8 \mathrm { km } {/tex} and then coming back would be

Question 35 :
A body {tex} A {/tex} begins to move with initial velocity {tex}2 \mathrm { m } / \mathrm { sec } {/tex} and continues to move at a constant acceleration {tex} a \cdot \Delta t = 10 \mathrm { seconds } {/tex} after the body {tex} A {/tex} begins to move a body {tex} B {/tex} departs from the same point with an initial velocity {tex} 12 \mathrm { m } / \mathrm { sec } {/tex} and moves with the same acceleration {tex} a {/tex}. What is the maximum acceleration {tex} a {/tex} at which the body {tex} B {/tex} can overtake {tex} A ? {/tex}

Question 36 :
It was calculated that a shell when fired from a gun with a certain velocity and at an angle of elevation {tex} 5 \pi / 36 {/tex} rad should strike a given target. In actual practice, it was found that a hill just prevented the trajectory. At what angle (rad) of elevation should the gun be fired to hit the target

Question 37 :
A particle crossing the origin of co-ordinates at time {tex} \mathrm { t } = 0 , {/tex} moves in the xy-plane with a constant acceleration {tex}a{/tex} in the y-direction. If its equation of motion is {tex} \mathrm { y } = \mathrm { bx } ^ { 2 } {/tex} (b is a constant), its velocity component in the x-direction is

Question 38 :
For motion in two or three dimensions, the angle between velocity and acceleration is

Question 39 :
If the sum of two unit vectors is a unit vector, then the magnitude of their difference is

Question 40 :
If {tex} \overrightarrow { \mathrm { A } } = \hat { \mathrm { i } } + \hat { \mathrm { j } } + \hat { \mathrm { k } } {/tex} and {tex} \overrightarrow { \mathrm { B } } = 2 \hat { \mathrm { i } } - \hat { \mathrm { j } } + 4 \hat { \mathrm { k } } {/tex} then the unit vector along {tex} \overrightarrow { \mathrm { A } } + \overrightarrow { \mathrm { B } } {/tex} is