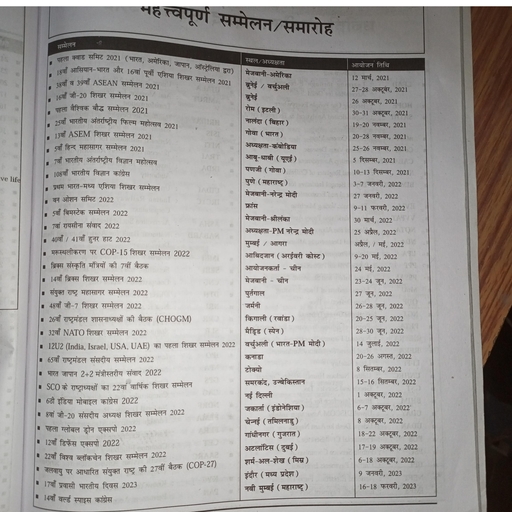
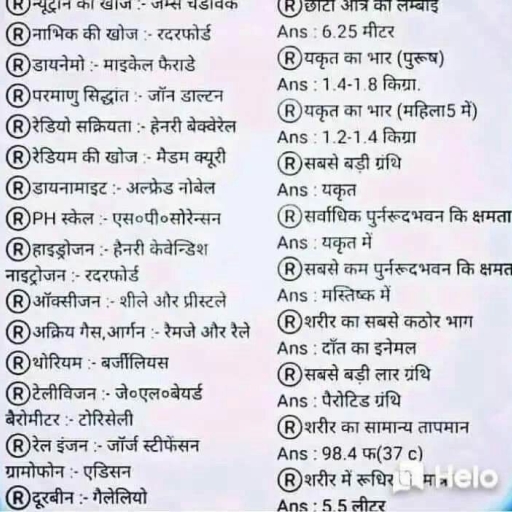
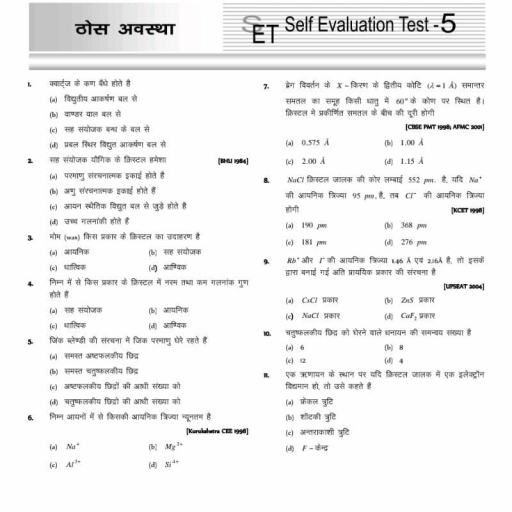
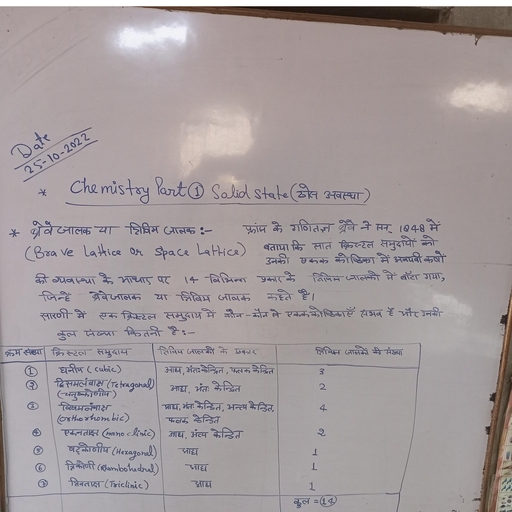
Question 1 :
A sign convention is used, the positive direction for position, velocity and acceleration is upward. A ball of mass m is thrown upward with velocity $V$ and caught during returning. Identify the signs of position, velocity and acceleration during descending part of the trajectory.<table class="wysiwyg-table"><tbody><tr><td></td><td>Position</td><td>Velocity</td><td>Acceleration</td></tr><tr><td>(A)</td><td>Positive </td><td>Positive</td><td>Positive</td></tr><tr><td>(B)</td><td>Positive</td><td>Positive</td><td>Negative</td></tr><tr><td>(C)</td><td>Positive</td><td>Negative</td><td>Negative</td></tr><tr><td>(D)</td><td>Negative</td><td>Positive</td><td>Negative</td></tr><tr><td>(E)</td><td>Negative</td><td>Negative</td><td>Negative</td></tr></tbody></table>
Question 2 :
The same retarding force is applied to stop a train. If the speed is doubled, then the distance will be
Question 3 :
A motorcycle is moving with a velocity 80km/hr ahead of a car moving with a velocity of 65 km/hr in the same direction. What is the relative velocity of the motorcycle with respect to the car :-
Question 4 :
A stone dropped from the roof of a building takes 4 s to reach the ground. The height of the building is.
Question 5 :
Three bodies $A, B$ and $C$ are moving in a straight line in the same direction such that relative velocity of $A$ w.r.t $B$ is $2m/s$, relative velocity of $B$ w.r.t $C$ is $5m/s$.<br/>Find the relative velocity of $C$ w.r.t $A$. 
Question 6 :
The acceleration of a body projected upwards with a certain velocity is equal to :
Question 7 :
If a body is thrown up with an initial velocity u and covers a maximum height of h, then h is equal to
Question 8 :
A body falls from a height $h=200\ m$.The ratio of distance travelled in each $2 sec$ during $t=0$ to $t=6\ sec$ of the journey is
Question 9 :
Consider a jet traveling at 1000 km/hr. If the jet shoots a laser in the same direction it is traveling, how fast will the laser be traveling relative to the ground?<br>
Question 10 :
A purple car is moving three times as fast as a yellow car. Each car slows down to a stop with the same constant acceleration.<br>How much more distance is required for the purple car to stop?
Question 11 :
<p>A helicopter is flying south with a speed of $50\ kmh^{-1}$. A train is moving with the same speed towards east. The relative velocity of the helicopter as seen by the passengers in the train will be $50 \sqrt {2}\ kmh^{-1}$ towards</p>
Question 12 :
A ball is dropped from a certain height, and at that exact same moment a rock is fired horizontally from the exact same height above ground level.<br>Assuming that air resistance is negligible, which object will strike the ground first?
Question 13 :
Two stones are dropped from the top of a tower at half a second apart. The time after dropping the first stone at which the distance between the two stones is 20 m is $(g = 10 ms^{-2})$
Question 14 :
A block is released from rest at the top of a frictionless inclined plane 16 m long. It reaches the bottom 4 sec later. A second block is projected up the plane from the bottom at the instant the block is released in such a way that it returns to the bottom simultaneously with first block. The acceleration of each block on the incline is
Question 15 :
A body is thrown vertically upwards and rises to a height of $10 m$. The time taken by the body to reach the highest point is
Question 16 :
Two bodies of masses $20 kg$ and $15 kg$ are dropped from the top of a building. At any instant during the fall, which of the following properties that both the bodies posses is equal in magnitude?
Question 17 :
How do the directions of velocity and acceleration act when brakes are applied to a moving cycle?
Question 18 :
<p>A sign convention is used, the positive direction for position, velocity and acceleration is upward. A ball of mass m is thrown upward with velocity $V$ and caught during returning. Identify the signs of position, velocity and acceleration during ascending part of the trajectory.<br/></p><table class="wysiwyg-table"><tbody><tr><td></td><td>Position</td><td>Velocity</td><td>Acceleration</td></tr><tr><td>(A)</td><td>Positive</td><td>Positive</td><td>Positive</td></tr><tr><td>(B)</td><td>Positive</td><td>Positive</td><td>Negative</td></tr><tr><td>(C)</td><td>Positive</td><td>Negative</td><td>Negative</td></tr><tr><td>(D)</td><td>Negative</td><td>Positive</td><td>Negative</td></tr><tr><td>(E)</td><td>Negative</td><td>Negative</td><td>Negative</td></tr></tbody></table>
Question 19 :
When two bodies move uniformly towards each other, the distance decreases by $6ms^{-1}$.If both bodies move in the same direction with the same speed as above the distance between them increases by $4ms^{-1}$. Then the speed of the two bodies are
Question 20 :
A toy rocket is launched straight up. At the exact top of its flight path, which of the following is true?
Question 21 :
A bowling ball is rolling westward and slowing down as it approaches the end of the alley. The direction of the bowling ball's acceleration is :
Question 22 :
A body falls freely for $10 sec$. Its average velocity during this journey (take $g=10m{s}^{-2}$):
Question 23 :
A rock falls off top of a building and drops to the ground in 3 m 20 sec. what is the height of the building?
Question 24 :
A ball is released from the top of a height $h$. It takes time $T$ to reach the ground. What is the position of the ball (from ground) after time $\frac{T}{3}$
Question 26 :
A block of mass $2\ kg$ starts moving with initial speed of $10\ m/s$ and accelerates at $-2 m/s^2$. How far does the object travel before coming to rest? <br/>
Question 27 :
A bus moving with a speed of $10m/s$ on a straight road. A scooterist wishes to overtake the bus in $100s$. If the bus is at a distance of $1km$ from the scooterist, with what speed should the scooterist chase the bus?
Question 28 :
At an airport, a bored child starts to walk backwards on a moving platform. The child accelerates relative to the platform with $a=-0.5{m}/{{s}^{2}}$ relative to the platform.<br>The platform moves with a constant speed $v=+1.0{m}/{s}$ relative to the stationary floor.<br>In $4.0$ seconds, how much will the child have been displaced relative to the floor?
Question 29 :
A ball is dropped off a high building and strikes the ground with an impact velocity of 30 m/s. Calculate the height of building :<br/>
Question 30 :
A rubber ball dropped from a certain height is an example of
Question 31 :
A helicopter is flying south with a speed of $50\, km h^{-1}$. A train is moving at the same speed towards east. The relative velocity of the helicopter as seen by the passengers in the train will be towards
Question 32 :
A ball is thrown upward with a velocity of 100m/s it will reach the ground after :-
Question 33 :
An iron ball and a wooden ball of the same radius are released from a height H in vacuum. The times taken by both of them of reach the ground are
Question 34 :
A stone is dropped from a building and $2$ seconds later another stone is dropped. How far apart are these two stones by the time the first one reaches a speed of $30m{ s }^{ -1 }$? (Take $g=10m{ s }^{ -2 }$)
Question 35 :
A ball is thrown vertically upward with speed $10$ m/s and it returns to the ground with speed $8$ m/s. A constant air resistance acts. The maximum height attained by the ball is?
Question 36 :
Two particles A and B having different masses are projected from a tower with same speed. A is projected vertically upward and B vertically downward. On reaching the ground.<br>
Question 37 :
A train is moving towards east and a car is along north, both with same speed. The observed direction of car to the passenger in the train is 
Question 38 :
If an iron ball and a wooden ball of the same radius are released from a height h in vaccum then time taken by both of them to reach ground will be:-
Question 39 :
The acceleration of a body projected upwards with a certain velocity is
Question 40 :
A body is thrown up with an initial velocity u and it covers a maximum height of h, then h is equal to
Question 41 :
A body is thrown vertically upwards and rises to a height of 10 m. The velocity with which the body was thrown upwards is $\displaystyle \left( g=9.8{ m }/{ { s }^{ 2 } } \right) $
Question 42 :
When a man stands on a moving escalator he goes up in $50\ sec.$ and when he walks up the moving escalator he goes up in $30\ sec.$ Then the man walks up the stationary escalator in a time of $----sec$
Question 43 :
A passenger in a moving train tosses a coin. If the coin falls behind him, the train must be moving with
Question 44 :
A stone falls from a balloon that is descending at a uniform rate of $12ms^{-1}$. The displacement of the stone from the point of release after 10sec is :-
Question 45 :
A ball is thrown directly upwards and reaches a maximum height $h$. When it is at height ${h}/{2}$, its speed relative to the initial speed ${v}_{0}$ it had when it was originally thrown is:
Question 46 :
A boy can throw a stone up to a maximum height of 10 m. The maximum horizontal distance that boy throw the same stone up will be
Question 47 :
A ball is thrown vertically up. If the ball reached at maximum height in $3s$. Assume air resistance is negligible. The initial velocity of the ball is most nearly :
Question 48 :
A team of skydivers jumps from a plane and holds hands to form a flower-like design. As the skydivers begin their free fall, their velocity increases and their:
Question 50 :
A stone is dropped from a tower. It was found that it covered a distance of $45m$ during its last second of the fall. Calculate the time of the fall and the height of the tower? $\left( g=10m{ s }^{ -2 } \right) $
Question 51 :
Assertion - The sound emitted by the source travels in all directions.<br>Reason - The relative velocity of sound with respect to the observer is the sum of velocity of sound and velocity of observer.<br>
Question 53 :
A metal ball falls from a height of 1 m on to a steel plate and jumps upto a height of 81 cm. The coefficient of restitution of the ball material is?
Question 54 :
Assertion: Acceleration and displacement are in the opposite direction during retardation.
Reason: Acceleration is given as the change in velocity per unit time.
Question 55 :
Upton Chuck is riding the Giant Drop at Great America. If Upton free falls for $2.60$ seconds, then how far will he fall? (in m)<br/>
Question 56 :
A body thrown vertically up reaches a maximum height of 50 m. Another body with double the mass thrown up with double the initial velocity will reach a maximum height of :<br/>
Question 57 :
A body is projected vertically up with u. Its velocity at half its maximum height is?
Question 58 :
A car is standing $200m$ behind a bus, which is also at rest. The two start moving at the same instant but with different forward accelerations. The bus has acceleration $2m/{s}^{2}$ and the car has acceleration $4m/{s}^{2}$. The car will catch up with the bus after a time of:
Question 59 :
The position of an object moving along x-axis is given by x = a + $bt^2$, where a = 8.5 m and b = 2.5 m $s^{-2}$ and t is measured in seconds. The average velocity of the object between t = 2 s and t = 4 s is
Question 60 :
At time $t = 0$, two bodies A and B are at the same point. A moves with constant velocity $V$ and B starts from rest and moves with constant acceleration. Relative velocity of B with respect to A when the bodies meet each other is:
Question 61 :
A cart begins from rest at the top of a long incline and rolls with a constant acceleration of $2m/s^{2}$. How far has the cart moved along the incline after rolling for $3$ seconds?
Question 62 :
Two bodies are projected simultaneously from the same point, in the same vertical plane, one towards east and other towards west with velocities $8ms^{-1}$and $2ms^{-1}$ respectively. The time at which their velocities are perpendicular to each other is
Question 63 :
A fire extinguishing hose pipe disposes watch at a speed of 10 m/s to put off fire on a building. Assuming safe distance from the building on ground is 5 m, What is the maximum height at which water strikes building?
Question 64 :
A particle is projected vertically upwards and it attains maximum height $H$. If the ratio of times to attain height $h(h < H)$ is $1/3$, then $h$ equals
Question 65 :
If the velocity of a particle is given by $4\hat{i} + 5 t\hat{j}$, then the magnitude of its acceleration is ......
Question 66 :
A stone falls freely from rest from a height h and it travels a distance $\dfrac { 9h }{ 25 } $ in the last second. The value of h is :
Question 67 :
A particle is thrown upwards with velocity $2$ m/s, the velocity of particle after $2$ s is :
Question 68 :
The function which represents the height, $h(t)$, of a ball t seconds after it is kicked into the air is<br/>$h(t)\, =\, - 16t^2\, +\, 64t$.<br/>What does $t$ represent if $h(t)$ is zero ?
Question 69 :
A particle is moving in a straight line whose position varies with time as $x=8t^2+\dfrac{2}{\pi}\sin \pi t$, where x is in meter and t is in second. Then the position, velocity and acceleration of a particle at $t=4$s respectively are?
Question 70 :
A rocket is fired and ascends with constant vertical acceleration of $10m/s^{2}$ for 1 minute. Its fuel is exhausted and it continues as a free particle.The maximum altitude reached is ($g=10m/s^{2}$)
Question 71 :
A car moving with a speed of $50\ km/hr$, can be stopped by brakes after at least $6\ m$. If the same car is moving at a speed of $100\ km/hr$, the minimum stopping distance is:
Question 72 :
A police party is moving in a jeep at a constant speed $v$. They saw a thief at a distance x on a motorcycle which is at rest. The moment the police saw the thief, the thief started at constant acceleration $a$. Which of the following relations is true if the police is able to catch the thief?
Question 73 :
A ball is projected vertically up with a velocity of $20 ms^{-1}$. Its velocity, when the displacement is $15 m$, is......... $ms^{-1}.$ (Take  $g = 10 ms^{-2}$)<br/>
Question 74 :
When a bus driver travelling at a speed of 20m/s applied brakes and brings the bus to rest in 10 seconds, then retardation will be
Question 75 :
Two balls are dropped from the same point after an interval of $1$ second. Their separation $3$ second after the release of the second ball. ($g = 10 m/s$ $^2$)
Question 76 :
Two trains along the same straight rails moving with constant speed $60\ km/hr$ and $30\ km/hr$ respectively toward each other. If at time $t=0$, the distance between them is $90\ km$, the time when they collide is
Question 77 :
A body moves with uniform velocity of $u=7\;m/s$ from $t=0\;to\;t=1.5 s$. It starts moving with an acceleration of $10\;m/s^{2}$. The distance between $t=0\;to\;t=3s$ will be:
Question 78 :
An object, moving with a speed of $6.25 \; ms^{-1}$, is decelerated at a rate given by $\dfrac{dv}{dt}=-2.5\sqrt{v}$ where $v$ is the instantaneous speed. The time taken by the object, to come to rest, would be <br>
Question 79 :
A ball of mass $m$ is thrown vertically upwards. Another ball of mass $2m$ is thrown simultaneously at an angle $\theta$ with horizontal. Both of them hit the ground at the same time when thrown from the same height. The heights attained by the two are in the ratio ?
Question 80 :
A ball is dropped from height h and another from 2h. The ratio of time taken by the two balls to reach the ground is:
Question 81 :
$A$ starts from rest and moves with an acceleration $a_{1}$. Two seconds later$,\ B$ starts from rest and moves with an acceleration $a_{2}$. If the displacement of $A$ in the $5^{th}$ second is the same as that of $B$ in the same interval, the accelerations $a_{1}$ and $a_{2}$ are<br>
Question 82 :
A body dropped from the top of a tower reaches the ground in 4 s. The height of the tower could be :
Question 83 :
When a ball is thrown up vertically with velocity $ {v}_{o} $<b> </b>it reaches a maximum height of $h$. If one wishes to triple the maximum height then the ball should be thrown with velocity.<br/>
Question 84 :
If a body starts from rest and moves with uniform acceleration, then the displacement of the body is directly proportional to the cube of the time.<br/>
Question 85 :
A stone is released from a hot air balloon which is rising steadily with a velocity of $\displaystyle { 4\quad ms }^{ -1 }$. The velocity of the stone at the end of 3 s after it is released is _____ $\displaystyle { ms }^{ -1 }$
Question 86 :
The retardation experienced by moving motorboat after its engine is cut off at the instant $t = 0$ is given by $a = -\alpha v^3$ where $\alpha$ is a positive constant with appropriate dimensions. If velocity at $t = 0$ is $v_0$ , then velocity as a function of time is given as
Question 87 :
A particle is projected vertically upwards from a point $A$ on the ground. It takes $ { t }_{ 1 } $ time to reach a point $B$ but it still continues to move up. If it takes further $ { t }_{ 2 } $ time to reach the ground from point $B$ then height of point $B$ from the ground is<br>
Question 88 :
Upton Chuck is riding the Giant Drop at Great America. If Upton free falls for $2.60$ seconds, what will be his final velocity? (in m/s)
Question 89 :
A body covers $26, 28, 30$ and $32$ meters in $10^{ th }$, $11^{th}, 12^{ th }$ and ${ 13 }^{ th }$ seconds respectively. The body starts
Question 91 :
A car and a lorry are moving with the same momentum, if the same braking force is applied, then: 
Question 92 :
If the distance travelled by a freely falling body in the last second of its journey is equal to the distance travelled in the first $2$ s, the time of descent of the body is
Question 93 :
If the ratio of distances travelled by freely falling body in the last and last but one second of its motion is $7:5$. The velocity with which the body strikes the ground is : (Given $g=9.8 \;ms^{-2}$)<br/>
Question 95 :
A time $t = 0$ a particle starts moving along the x axis. If its kinetic energy increases uniformly with $t$, the net force acting on it must be
Question 96 :
A car is travelling at 30 m/s. If its velocity increases to 50 m/s while accelerating at the rate of 2.5 m/s$\displaystyle ^{2}$ find the time taken to reach that velocity.
Question 97 :
A ball is vertically downwards with a speed of 6 m/s from a hight of 3.2 m. It strikes a horizontal floor and rebounds back to the same height. The value of corfficient of restitutions (e) is :-
Question 98 :
Three force $\vec {F_{1}}=(2\hat {i}+4\hat {j})\ N:\vec {F_{2}}=(2\hat {i}-4\hat {j})\ N$ and $\vec {F_{3}}=(\hat {k}-4\hat {i}-2\hat {j})\ N$ are applied on an object of mass $1\ kg$ at rest at origin. The position of the object at $t=2s$ will be
Question 99 :
A ball after having fallen from rest under the influence of gravity for $6s$, crashes through a horizontal glass plate, thereby losing two-third of its velocity. Then it reaches the ground in $2s$, height of the plate above the ground is
Question 100 :
From the top of a tower, a particle is thrown vertically downwards with a velocity of $10\ m/s$. The ratio of the distances, covered by it in the $3^{rd}$ and $2^{nd}$ seconds of the motion is (Take $g = 10 m/s^{2})$.
Question 101 :
A ball is thrown vertically upwards with a velocity of $10 ms^-1$. IT returns to the ground with a velocity of$ 9 ms^-1$. If $g = 9.8 ms^-2$, then the maximum height attained by the ball is nearly ( assume a resistance to be uniform)
Question 102 :
A machine gun is mounted on a $2000 kg $ vehicle on a horizontal smooth road (friction negligible). The gun fires $10 $ bullets per sec with a velocity of $500 m/s $ . If the mass of each bullet be $10 g $ , what is the acceleration produced in the vehicle?
Question 103 :
A swimmer is capable of swimming $1.65$ $ms^{-1}$ in still water. If she swims directly across a $180$m wide river whose current is $0.85$ m/s, how far downstream(from a point opposite her standing point) will she reach?
Question 104 :
A stone thrown upwards with speed $u$ attains maximum height $h$. Another stone thrown upwards from the same point with sapped $2u$ attains maximum height $H$. What is the relation between $h$ and $H$?
Question 105 :
A swimmer's speed in the direction of flow of river is $ 16 kmh^{-1} $ . Against the direction of flow of river, the swimmer's speed is $8 kmh^{-1} $ Calculate the swimmer's speed in still water and the velocity of flow of the river.
Question 106 :
A truck travelling due to north at $30\ m/s$ turns west and travels at the same speed, then the change in velocity is :
Question 107 :
Two particles $A$ and $B$ start moving with velocities $20\ m/s$ and $30\sqrt{2}\ m/s$ along $x-axis$ and at an angle $45^{o}$ with $x-$axis respectively in $xy-plane$ from origin. The relative velocity of $B$ w.r.t. $A$
Question 108 :
Two parallel rail tracks run north-south. Train $A$ moves north with a speed of $54\ km{h}^{-1}$ and train $B$ moves south with a speed of $90\ km{h}^{-1}$. The relative speed of $B$ with respect to $A$ is:
Question 109 :
A stone A is dropped from a height h above the ground. A second stone B is simultaneously thrown vertically up from a point on the ground with velocity v. The line of motion of both the stones is same. The value of v which would enable the stone B to meet the stone A midway ( at midpoint) between their initial position is:
Question 110 :
The wheels of an airplane are set into rotation just before landing so that the wheels do not slip on the ground. If the airplane is travelling in the east direction, what should be the direction of angular velocity vector of the wheels?
Question 111 :
Consider a collection of a large number of particles each with speed $v$. The direction of velocity is randomly distributed in the collection. The magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is <br/>
Question 112 :
A jet airplane travelling from east to west at a speed of $500\,km\ h^{-1}$ eject out gases of combustion at a speed of $1500\ km\ h^{-1}$ with respect to the jet plane. What is the velocity of the gases with respect to an observer on the ground?
Question 113 :
A "moving sidewalk" in a busy airport terminal moves $1 m/s$ and is $200 m$ long. A passenger steps onto one end and walks, in the same direction as the sidewalk is moving, at a rate of $2.0 m/s$ relative to the moving sidewalk. How much time does it take the passenger to reach the opposite end of the walkway? (in seconds)
Question 114 :
A man of $80 kg$ attempts to jump from a small boat of mass $40 kg$ on to the shore. He can generate a relative velocity of $6 m/s $ between himself and boat. His velocity towards the shore is:
Question 115 :
If the plane has an eastward heading, and a $20 m/s$ wind blow towards the southwest, then the plane's speed is-
Question 116 :
Four persons A, B, C and D at the corners of an square of side $X$ move at a constant speed $V$. Each person maintains a direction towards the person at the next corner. The time, the persons take to meet each other is
Question 117 :
There is a regular bus service between towns A and B, with a bus leaving towns A and B every $T$ minutes. A cyclist moving with a speed of $20\ km h^{-1}$ in the direction A to B notices that a bus goes past him every $18  mins$ in his direction and every $6  mins$ in the opposite direction. What is the period $T$ of bus service?
Question 118 :
A juggler tosses a ball up in the air with speed $u$ . At the instant it reaches its maximum height $H$ , he tosses up a second ball with the same initial speed. The two balls will collide at a height.
Question 119 :
Two bodies are thrown vertically upward, with the same initial velocity of $98\ m/s$ but $4\ sec$ apart. How long after the first one is thrown when they meet ?
Question 120 :
A train is moving at a constant speed V when its driver observes another train in front of him on the same track and moving in the same direction with constant speed v. If the distance between the trains is x, then what should be the minimum retardation of the train so as to avoid collision?
Question 121 :
Two particles A and B are shot from the same height at $t=0$ in opposite directions with horizontal velocities $3m/s$ and $4m/s$ respectively. If they are subjected to the same vertical acceleration due to gravity ($g=9.8m/{s}^{2}$). the distance between them when their velocity vectors become mutually perpendicular is:
Question 122 :
A bus is moving with a speed of $10ms^{-1}$ on a straight road. A scooterist wishes to overtake the bus in 100s. If the bus is at a distance of 1 km from the scooterist, with what speed should the scooterist chase the bus ?<br>
Question 123 :
A stone is dropped from a height h. Simultaneously, another stone is thrown up from the ground which reaches a height of $4h$. The two stones cross each other after time
Question 124 :
The driver of a train moving with a constant speed $v_1$ along a straight track sights another train at a distance d ahead of him on the same track moving in the same direction with a constant speed $v_2$. He at once applies the brakes and gives his train a constant retardation f. There will be a collision of the trains if:<br>
Question 125 :
A police party is moving in a jeep at a constant speed $V$. They saw a thief at a distance $x$ on a motorcycle which is at rest. The moment the police saw the thief, the thief started at constant acceleration $a$. Which of the following relations is true if the police is able to catch the thief?<br/>
Question 126 :
A person walk up a stalled 15 m long escalator in 90 s. When standing on the same escalator, now moving, the person is carried up in 60 s. How much time would it take that person to walk up the moving escalator? Does the answer depend on the length of the escalator?<br>
Question 127 :
Two trains are moving with velocities $\displaystyle v_{1}=10\ ms^{-1}$ and $\displaystyle v_{2}=20\ ms^{-1}$ on the same track in opposite directions. After the application of brakes if their retarding rates are $\displaystyle a_{1}=2\ ms^{-2}$ and $\displaystyle a_{1}=1\ ms^{-2}$ respectively, then the minimum distance of separation between the trains to avoid collision is<br>
Question 128 :
Assertion: Displacement-time equation of two particles moving in a straight line are, $\displaystyle s_{1}=2t-4t^{2}$ and $\displaystyle s_{2}=2t+4t^{2}.$ Relative velocity between the two will go on increasing.
Reason: If velocity and acceleration are of same sign then speed will increase.
Question 129 :
The time in which the ball strikes the floor of elevator is given by<br>
Question 130 :
A thief in a stolen car passes through a police check post at his top speed of $\displaystyle 90\ kmh^{-1}.$ A motorcycle cop, reacting after $2\ s$, accelerates from rest at $\displaystyle 5\ ms^{-2}.$ His top speed being $\displaystyle 108\ kmh^{-1}.$ Find the maximum separation between policemen and thief.<br/>
Question 131 :
The driver of a train moving with a speed $v_{ 1 }$ sights another train at a distance $s$, ahead of him moving in the same direction with a slower speed $v_{ 2 }$. He applies the brakes and gives a constant deceleration $a$ to his train. For no collision, $s$ is<br>
Question 132 :
Two persons A and B running on a straight track in the same direction observe a car. A says that the car is moving in east direction and B says that the car is moving in north direction. They contradict the direction but say that magnitude is same. If the speed of B is double that of the speed of A, then the true direction of the car will be<br/>
Question 133 :
Two particles move in space with nonzero initial relative velocity and nonzero constant relative acceleration. Then :<br/>
Question 134 :
A particle is thrown up inside a stationary lift of sufficient height. The time of flight is $T$. Now it is thrown again with same initial speed $v_{0}$ with respect to lift. At the time of second throw, lift is moving up with speed $v_{0}$ and uniform acceleration $g$ upward (the acceleration due to gravity). The new time of flight is :<br/>
Question 135 :
N particles moving in a straight line have initial velocities of 1, 2, 3, ........... N m/s and accelerations of 1, 2, 3, ...... N m/s$^2$ respectively. If the initial spacing between any two consecutive particles is same then, select the correct alternative(s).<br/>
Question 136 :
distance travelled by the ball upto that instant, when lift and ball were of same height from ground Take $\displaystyle g= 10m/s^{2}$
Question 137 :
The driver of an express train travelling at a speed of $v_{1}$ sees on the same track at distance $d$ in front of him a goods train travelling in the same direction at a speed $v_{2}$ such that $v_1>v_2$. Immediately he applies brakes to his express train producing retardation $a$ to avoid collision. Then
Question 138 :
If six persons are at the corners of a regular hexagon of side $X$ move at a constant speed $V$. Each person maintains a direction towards the person at the next corner. The time, the persons will take to meet each other is
Question 139 :
The maximum height reached by ball, as measured from the ground would be<br>
Question 140 :
Two particles $P$ and $Q$ move in a straight line $AB$ towards each other. $P$ starts from $A$ with velocity $u_{1}$, and an acceleration $a_{1}$, $Q$ starts from $B$ with velocity $u_{2}$ and acceleration $a_{2}$.They pass each other at the midpoint of $AB$ and arrive at the other ends of $AB$ with equal <i></i>velocities
Question 141 :
Displacement of ball with respect to ground during its flight would be<br>
Question 142 :
The maximum separation between the floor of elevator and the ball during its flight would be <br>
Question 143 :
A man is driving at the speed $40 mph$ when he see an obstacle at distance $300 ft$ ahead of his position. The driver applies the brakes and decelerates at $10 ft/s^2$.How far from the obstacle will the driver be when he finally stops? (in metres)
Question 144 :
A man is driving at the speed $40 mph$ when he see an obstacle at distance $300 ft$ ahead of his position. The driver applies the brakes and decelerates at $10 ft/s^2$ How long does it take him to stop the vehicle? (in s)
Question 145 :
Ima Hurryin is approaching a stoplight moving with a velocity of $+30.0 m/s$. The light turns yellow, and Ima applies the brakes and skids to a stop. If Ima's acceleration is $-8.00 m/s^2$, then determine the displacement of the car during the skidding process. (Note that the direction of the velocity and the acceleration vectors are denoted by a $+$ and a $-$ sign.)
Question 146 :
A bullet travelling horizontally loses ${\dfrac{1}{20}^{th}}$ of its velocity while piercing a wooden plank. Number of such planks required to stop the bullet is:
Question 147 :
A car traveling at a speed $ 30 km h^{-1}$ is brought to a halt in 8 m by applying breaks. If the same car is traveling at $60 km h^{-1}$, it can be brought to a halt with the same breaking power in :
Question 148 :
A particle starts from the origin with a velocity of 10 m/s and moves with a constant acceleration till the velocity increases to 50 m/s. At that instant, the acceleration is suddenly reversed. What will be the velocity of the particle, when it returns to the starting point?
Question 149 :
A particle moves in circle of radius $9m$. Its linear speed is given by $v=3t$. What is the net acceleration of the partical at $T=2\ sec$.
Question 150 :
Two cars 1 & 2 starting from rest are moving with speeds $V_1 $ and $V_2 m/s (V_1 > V_2),$ car 2 is ahead of car '1' by 'S' metres when the driver of car '1' sees car '2'. What minimum retardation should be given to car '1' to avoid collision.