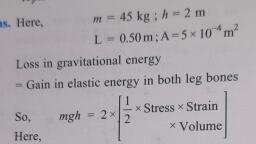Question 1 :
Two coherent monochromatic light beams of intensities '$4I$' and '$9I$' are superimposed. The maximum and minimum possible intensities in the resulting beam are

Question 2 :
In a two slit experiment with white light, a white fringe is observed on a screen kept behind the slits. When the screen is moved away by $0.05\ m$, this white fringe

Question 3 :
Wavelength of red lightis $7.5 \times 10^{-5}\ cm$ and that of blue light is$5.0 \times 10^{-5}\ cm$. The value of $n$ for which $(n+1)$ thblue bright band coincides with $n^{th}$ red band, is:<br>

Question 4 :
If white light is used in a Young's double slit experiment.

Question 5 :
If the intensities of the two interfering beams in Young's double-slit experiment are I$_{1}$ and I$_{2}$, then the contrast between the maximum and minimum intensities is good when

Question 6 :
In Young's experiment of double slit, the number&#160;of times the intensity of the central bright band&#160;greater than the individual intensity of the&#160;interfering waves :<br/>

Question 7 :
In YDSE ratio of width of slit is $4 : 1$, then ratio of maximum to minimum intensity

Question 8 :
In Young's double slit experiment, the slits are 2 mm apart and are illuminated by photons of two wavelengths $\lambda _{1}=12000\:A^{0}$ and $\lambda _{2}=10000\:A^{0}$. At what minimum distance from the common centralbright fringe on the screen 2 m from the slit will a bright fringe from one interference pattern coincide with abright fringe from the other?

Question 9 :
Two slits are separated by a distance of $0.5\ mm$ and illuminated with light of$\displaystyle \lambda =6000\overset { \circ }{ A }$. If the screen is placed $2.5\ m$ from the slits, the distance of the third bright image from the centre will be:<br>

Question 10 :
In Young's double-slit experiment, the density of light at a point on the screen, where the path difference is $\lambda$ is$I$. The intensity of light at s point where the path difference becomes $\lambda/3$ is

Question 11 :
In a Young's double slit experiment, $I_{0}$ is the&#160;intensity at the central maximum and $\beta $ is the&#160;fringe width. The intensity at a point P distant x&#160;from the centre will be:<br/>

Question 12 :
Choose the Correct answer from alternative given.<br/>Light from two coherent sources of the same amplitude A&#160; and wavelength $\lambda$ illuminates the screen. The intensity of the central maxima is $I_0$ . If the sources were incoherent, the intensity at the same point will be then:<br/>

Question 13 :
In an interference experiment, intensity ratio at the bright to dark fringe is $9 : 1$. Amplitudes of interfering waves was in the ratio.

Question 14 :
In a YDSE with identical slits, the intensity of the central bright fringe is ${I}_{0}$.If one of the slits is covered, the intensity at the same point is<br>

Question 15 :
In Young's double slit experiment with&#160;monochromatic source of light of wavelength&#160;6000 A$^{\circ}$, if the path difference at a point on the&#160;screen is 6 $\times$ $10^{-6}m$ the number of the bright&#160;band formed at that point is:<br/>

Question 16 :
Two slits spaced $0.25\ mm$ apart are placed $0.75\ m$ from a screen and illuminated by coherent light with a wavelength of $650\ nm$. The intensity at the center of the central maximum ($\theta={0}^{o}$) is ${I}_{0}$. The distance on the screen from the center of the central maximum to the point where the intensity has fallen to ${I}_{0}/2$ is nearly<br/>

Question 17 :
Two interfering waves have amplitudes in the ratio $5:1$. The ratio of the maximum to the minimum intensity is :<br/>