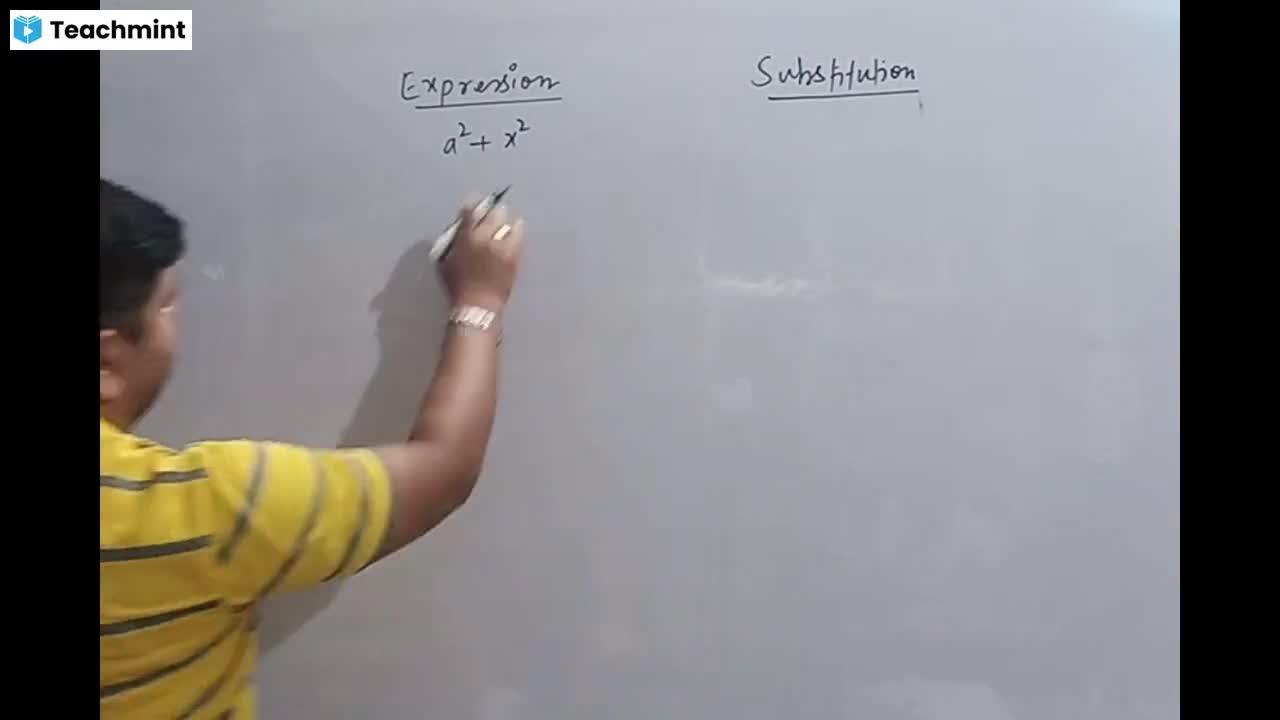Question 1 :
If 2x<sup>1/3</sup> + 2x<sup>-1/3</sup> = 5, then x is equal to -<br>
Question 2 :
If {tex} | z - 1 | \leq 2 {/tex} and {tex} \left| \omega z - 1 - \omega ^ { 2 } \right| = a {/tex} (where {tex} \omega {/tex} is a cube root of unity) then complete set of values of {tex} a {/tex} is
Question 3 :
The number of complex numbers {tex} z {/tex} satisfying {tex} | z - 3 - i | = | z - 9 - i | {/tex} and {tex} | z - 3 + 3 i | = 3 {/tex} are
Question 4 :
The locus of point {tex} z {/tex} satisfying {tex} \operatorname { Re } \left( \frac { 1 } { z } \right) = k , {/tex} where {tex} k {/tex} is a non- zero real number, is
Question 5 :
If {tex} \left( \frac { 1 + i } { 1 - i } \right) ^ { x } = 1 , {/tex} then
Question 6 :
For any complex number {tex} z , {/tex} maximum value of {tex} | z | - | z - 1 | {/tex} is
Question 7 :
If {tex} z _ { 1 } , z _ { 2 } , z _ { 3 } {/tex} are the vertices of an equilateral triangle {tex} A B C {/tex} such that {tex} \left| z _ { 1 } - i \right| = \left| z _ { 2 } - i \right| = \left| z _ { 3 } - i \right| , {/tex} then {tex} \left| z _ { 1 } + z _ { 2 } + z _ { 3 } \right| {/tex} equals to
Question 8 :
Number of solutions of the equation {tex} z ^ { 3 } + \frac { 3 ( \bar { z } ) ^ { 2 } } { | z | } = 0 {/tex} where {tex}z{/tex} is a complex number is
Question 9 :
If {tex} \left| z ^ { 2 } - 3 \right| = 3 | z | {/tex} then the maximum value of {tex} | z | {/tex} is
Question 10 :
If {tex} | z + 4 | \leq 3 , {/tex} then the maximum value of {tex} | z + 1 | {/tex} is
Question 11 :
The conjugate of a complex number is {tex} \frac { 1 } { i - 1 } {/tex}. Then that complex number is<br>
Question 12 :
If {tex} z = ( i ) ^ {{ ( i ) }^ {(i)}} \quad {/tex} where {tex} i = \sqrt { - 1 } , {/tex} then {tex} | z | {/tex} is equal to
Question 13 :
If for complex numbers {tex} z _ { 1 } {/tex} and {tex} z _ { 2 } , \arg \left( z _ { 1 } \right) - \arg \left( z _ { 2 } \right) = 0 , {/tex} then {tex} | z _ { 1 } - {/tex} {tex} z _ { 2 } | {/tex} is equal to
Question 14 :
If {tex} k > 0 , | z | = | w | = k {/tex} and {tex} \alpha = \frac { z - \bar { w } } { k ^ { 2 } + z \bar { w } } , {/tex} then {tex} \operatorname { Re } ( \alpha ) {/tex} equals
Question 15 :
If {tex} \omega ( \neq 1 ) {/tex} is a cube root of unity, and {tex} ( 1 + \omega ) ^ { 7 } = A + B \omega . {/tex} Then {tex} ( A , B ) {/tex} equals
Question 16 :
If {tex} { 'z' } {/tex} is complex number then the locus of {tex} { 'z' } {/tex} satisfying the condition {tex} | 2 z - 1 | = | z - 1 | {/tex} is
Question 17 :
The number of complex number z such that {tex} | z - 1 | = | z + 1 | = | z - i | {/tex} equals
Question 18 :
If {tex} \omega = \frac { z } { z - ( 1 / 3 ) i } {/tex} and {tex} | \omega | = 1 , {/tex} then {tex} z {/tex} lies on
Question 19 :
If {tex} | z | = 1 {/tex} then the point representing the complex number {tex} - 1 + {/tex} {tex} 3 z {/tex} will lie on
Question 20 :
If {tex} 8 i z ^ { 3 } + 12 z ^ { 2 } - 18 z + 27 i = 0 , {/tex} then
Question 21 :
If {tex} t {/tex} and {tex} c {/tex} are two complex numbers such that {tex} | t | \neq | c | , | t | = 1 {/tex} and {tex} z {/tex} {tex} = ( a t + b ) / ( t - c ) , z = x + i y . {/tex} Locus of {tex} z {/tex} is (where {tex} a , b {/tex} are complex numbers)
Question 22 :
If {tex} z = 3 / ( 2 + \cos \theta + i \sin \theta ) , {/tex} then locus of {tex} z {/tex} is
Question 23 :
If {tex} k + \left| k + z ^ { 2 } \right| = | z | ^ { 2 } \left( k \in R ^ { - } \right) , {/tex} then possible argument of {tex} z {/tex} is
Question 24 :
If {tex} z = ( \lambda + 3 ) - i \sqrt { 5 - \lambda ^ { 2 } } , {/tex} then the locus of {tex} z {/tex} is
Question 25 :
If {tex} x {/tex} and {tex} y {/tex} are complex numbers, then the system of equations {tex} ( 1 {/tex} {tex} + i ) x + ( 1 - i ) y = 1,2 i x + 2 y = 1 + i {/tex} has