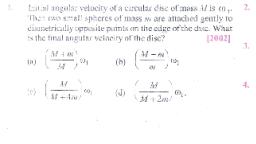Test Details

Maths

You have to attempt four test, 1) Maths 2)physics 3)chemistry 4)Bio Each test is of 20 min.

Jan 16, 11:35 AM

20 minutes

Jan 16, 11:55 AM

40.0 marks

MCQ

24 questions

YATI CLASSES

Mr. Avinash Tyagi founded Yati Classes in november, 2016 with the aim to help students preparing for IIT-JEE/NEET, realize their dreams, and to make sure that the preparation process itself becomes a fun filled and growth involving experience. The institute is successfully doing so and is now training many a hundred students. With high quality teaching It has produced Uttrakhand Rank 1 (3 times) and Roorkee rank 1 ( 5 times) in JEE Advanced and RMO, NTSE in the last 4 years now.

Class Details

Scholarship Test

Sarvottam 2022

Scholarship Test

More from YATI CLASSES

(20)

Test

Full Pattern Physics Test

crashcourse

Physics

0 Likes

3 Views

YATI CLASSES

May 23, 2022

Test

Physics Full Syllabus

crashcourse

Physics

0 Likes

11 Views

YATI CLASSES

May 13, 2022

Test

Bio Full Pattern Test

crashcourse

Physics

0 Likes

2 Views

YATI CLASSES

May 12, 2022

Test

Physics Full Test

crashcourse

Physics

0 Likes

3 Views

YATI CLASSES

May 10, 2022

Test

Full Pattern neet Test

crashcourse

Physics

0 Likes

0 Views

YATI CLASSES

May 10, 2022

Test

NEET Full Pattern TEST

crashcourse

Physics

0 Likes

5 Views

YATI CLASSES

May 01, 2022

Test

Electric Charges and Fields

neet

Physics

0 Likes

9 Views

YATI CLASSES

Apr 25, 2022

Test

NEET FULL TEST

crashcourse

Physics

0 Likes

1 Views

YATI CLASSES

Apr 17, 2022

Homework

AC Worksheet

crashcourse

Physics

0 Likes

20 Views

YATI CLASSES

Apr 07, 2022

Homework

Capacitance

crashcourse

Physics

0 Likes

27 Views

YATI CLASSES

Apr 01, 2022

Homework

Current Electricity

crashcourse

Physics

0 Likes

29 Views

YATI CLASSES

Mar 31, 2022

Homework

L C D

crashcourse

Maths

0 Likes

12 Views

YATI CLASSES

Mar 30, 2022

Test

Sets, Relations and Functions

crashcourse

Maths

0 Likes

2 Views

YATI CLASSES

Mar 27, 2022

Test

Current Electricity

crashcourse

Physics

0 Likes

1 Views

YATI CLASSES

Mar 27, 2022

Homework

Electrostats

crashcourse

Physics

0 Likes

42 Views

YATI CLASSES

Mar 25, 2022

Homework

Waves

crashcourse

Physics

0 Likes

23 Views

YATI CLASSES

Mar 23, 2022

Homework

SHM Worksheet

crashcourse

Physics

0 Likes

70 Views

YATI CLASSES

Mar 22, 2022

Homework

Straight Line

crashcourse

Maths

0 Likes

35 Views

YATI CLASSES

Mar 16, 2022

Homework

Mechanical Properties Of Matter

crashcourse

Physics

0 Likes

20 Views

YATI CLASSES

Mar 16, 2022

Homework

Rotational Motion

crashcourse

Physics

0 Likes

214 Views

YATI CLASSES

Mar 14, 2022

Recommended Content

(20)

Test

Function

class-2nd

0 Likes

16 Views

Deshmukh Sir's

Feb 16, 2022

Homework

Define Revision

class-7th

Science

0 Likes

2 Views

Md Mohid Akhtar

Feb 17, 2022

Test

Maths Test

class-2nd

Maths

0 Likes

12 Views

V P Sir

Feb 19, 2022

Test

Polinomial

class-10th

Maths

0 Likes

6 Views

Singh Gaurav

Nov 18, 2021

Test

Maths

class-2nd

Maths

0 Likes

3 Views

VIJAY PAL

Jan 29, 2022

Test

Carbon and its compounds

class-10th

Englishchembio

0 Likes

9 Views

P P Sir

Jan 13, 2022

Homework

Maths Assessment

class-2nd

Maths

0 Likes

146 Views

Tanusree ma'am

Oct 27, 2021

Test

Maths Test (Chapter-9)

class-3rd

Maths

0 Likes

3 Views

Anamika Tiwari

Feb 09, 2022

Test

Test 5

class-2nd

Pcmb

0 Likes

2 Views

Dr. Nitin Dighore

Apr 05, 2022

Test

MATHS OLYMPIAD

mathsolympiad

Mentalmaths

0 Likes

44 Views

Monika Kumari

Oct 23, 2021

Homework

Poorvitha

class-6th

Chemistry

0 Likes

8 Views

poorvitha. R

Jan 08, 2022

Homework

Maths ans Physics

class-9th

Allsubjects

0 Likes

0 Views

Himanshu

Jan 26, 2022

Test

JR JEE TEST NO-11

class-2nd

Physics

0 Likes

66 Views

srinivasa Naidu vegi

Nov 28, 2021

Test

Maths

class-10th

Math1

0 Likes

20 Views

Swapnil Patil

Oct 27, 2021

Test

MHTCET 22 Test 6

class-2nd

Pcmb

1 Likes

33 Views

Dr. Nitin Dighore

Apr 07, 2022

Homework

Maths Test

class-2nd

Allsubject

0 Likes

37 Views

Anupama

Feb 10, 2022

Homework

Maths

class-2nd

Mathematics

0 Likes

17 Views

Rubeena Gawri

May 18, 2022

Test

MATHS

class-2nd

Allsubjects

0 Likes

6 Views

Ritu Tiwari

Jan 05, 2022

Test

Lesson 1 and 2

class-4th

Science

0 Likes

6 Views

Payal Kumari

Jan 21, 2022

Test

Maths Unit Test

class-7th

Maths

1 Likes

66 Views

Kanika srivastava

Jan 31, 2022

Question Text

Question 1 :
Use Euclid's division algorithm to find the HCF of :$196$ and $38220$

Question 2 :
If $a=107,b=13$ using Euclid's division algorithm find the values of $q$ and $r$ such that $a=bq+r$

Question 3 :
Using the theory that any positive odd integers are of the form $4 q + 1$ or $4 q + 3$ where $q$ is a positive integer. If quotient is $4$, dividend is $19$ what will be the remainder?

Question 4 :
If HCF of $210$ and $55$ is of the form $(210) (5) + 55 y$, then the value of $y$ is :

Question 5 :
What must be subtracted from $4x^4 - 2x^3 - 6x^2 + x - 5$, so that the result is exactly divisible by $2x^2 + x - 1$?

Question 6 :
What must be added to $x^3-3x^2-12x + 19$, so that the result is exactly divisible by $x^2 + x-6$?

Question 8 :
When $(x^{3} - x^{2} - 5x - 3)$ is divided by $(x - 3)$, the remainder is

Question 9 :
Find the quadratic equation in $x$, whose solutions are $3$ and $2$.

Question 10 :
Let $p,q\in \left\{ 1,2,3,4 \right\} $. The number of equations of the form $p{ x }^{ 2 }+qx+1=0$ having real roots is

Question 11 :
State true or false For any arithmetic progression, when a fixed number is added or subtracted to each term, the resulting sequence still remains an A.P. with the common difference remaining unchanged.

Question 12 :
How many terms of the sequence $18, 16, 14,....$ should be taken so that their sum is zero?

Question 13 :
If the curve $y=ax^2+bx$ passes through $(-1, 0)$ and $y=x$ is the tangent line at $x=1$ then $(a, b)$.

Question 14 :
If the angle between the tangent from $(0,0)$ to the circle ${x}^{2}+{y}^{2}+10x+10y+40=0$ is ${\tan}^{-1}(m)$, then $m=$

Question 15 :
The sum of the radii of two circle is $140\ cm$ and the difference of their circumference is 88 cm. Find the radii of the two circles.

Question 17 :
A tent of 20 mm in radius and 14 mm in height has to be made. If the cost of canvas is Rs. 14 per $mm^2$, total cost of canvas used to make the tent is Rs. ____________. ( Use $\pi$ = 22/7)

Question 18 :
A bucket is in the shape of the frustum of a right circular cone, whose radii are $6$mm and $24$ mm. The curved surface area is $450$mm. Find the slant height. (Use $\pi = 3$).

Question 19 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b19a49273b230584979914.PNG' /> In the above figure, if TP and TQ are the two tangents to a circle with centre O so that ∠ POQ = 110°, then ∠ PTQ is equal to

Question 20 :
Is it TRUE or FALSE, that the length of tangent from an external point on a circle is always greater than the radius of the circle?

Question 21 :
The zeroes of the quadratic polynomial, whose sum and product of the zeroes are $\sqrt{2}$ and $-\frac{3}{2}$ respectively, are:

Question 22 :
Find a quadratic polynomial whose sum and product respectively of the zeroes are as given: $-\frac{8}{3}$, $\frac{4}{3}$

Question 23 :
State whether the given statement is true or false:The graph of a linear equation in two variables need not be a line.

Question 24 :
Find the value of x and y using cross multiplication method: $3x - 5y = -1$ and $x + 2y = -4$

More from YATI CLASSES

Recommended Content

Learn from Anywhere on Any Device