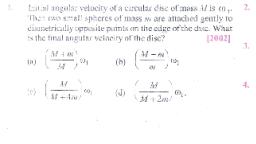Test Details

Sarvottam-YATI CLASSES ADMISSION TEST

Jan 30, 12:45 PM

30 minutes

Jan 30, 1:15 PM

30.0 marks

MCQ

15 questions

YATI CLASSES

Mr. Avinash Tyagi founded Yati Classes in november, 2016 with the aim to help students preparing for IIT-JEE/NEET, realize their dreams, and to make sure that the preparation process itself becomes a fun filled and growth involving experience. The institute is successfully doing so and is now training many a hundred students. With high quality teaching It has produced Uttrakhand Rank 1 (3 times) and Roorkee rank 1 ( 5 times) in JEE Advanced and RMO, NTSE in the last 4 years now.

Class Details

Scholarship Test

Sarvottam 2022

Scholarship Test

More from YATI CLASSES

(20)

Test

Full Pattern Physics Test

crashcourse

Physics

0 Likes

3 Views

YATI CLASSES

May 23, 2022

Test

Physics Full Syllabus

crashcourse

Physics

0 Likes

11 Views

YATI CLASSES

May 13, 2022

Test

Bio Full Pattern Test

crashcourse

Physics

0 Likes

2 Views

YATI CLASSES

May 12, 2022

Test

Physics Full Test

crashcourse

Physics

0 Likes

3 Views

YATI CLASSES

May 10, 2022

Test

Full Pattern neet Test

crashcourse

Physics

0 Likes

0 Views

YATI CLASSES

May 10, 2022

Test

NEET Full Pattern TEST

crashcourse

Physics

0 Likes

5 Views

YATI CLASSES

May 01, 2022

Test

Electric Charges and Fields

neet

Physics

0 Likes

9 Views

YATI CLASSES

Apr 25, 2022

Test

NEET FULL TEST

crashcourse

Physics

0 Likes

1 Views

YATI CLASSES

Apr 17, 2022

Homework

AC Worksheet

crashcourse

Physics

0 Likes

20 Views

YATI CLASSES

Apr 07, 2022

Homework

Capacitance

crashcourse

Physics

0 Likes

27 Views

YATI CLASSES

Apr 01, 2022

Homework

Current Electricity

crashcourse

Physics

0 Likes

29 Views

YATI CLASSES

Mar 31, 2022

Homework

L C D

crashcourse

Maths

0 Likes

12 Views

YATI CLASSES

Mar 30, 2022

Test

Sets, Relations and Functions

crashcourse

Maths

0 Likes

2 Views

YATI CLASSES

Mar 27, 2022

Test

Current Electricity

crashcourse

Physics

0 Likes

1 Views

YATI CLASSES

Mar 27, 2022

Homework

Electrostats

crashcourse

Physics

0 Likes

42 Views

YATI CLASSES

Mar 25, 2022

Homework

Waves

crashcourse

Physics

0 Likes

23 Views

YATI CLASSES

Mar 23, 2022

Homework

SHM Worksheet

crashcourse

Physics

0 Likes

70 Views

YATI CLASSES

Mar 22, 2022

Homework

Straight Line

crashcourse

Maths

0 Likes

35 Views

YATI CLASSES

Mar 16, 2022

Homework

Mechanical Properties Of Matter

crashcourse

Physics

0 Likes

20 Views

YATI CLASSES

Mar 16, 2022

Homework

Rotational Motion

crashcourse

Physics

0 Likes

214 Views

YATI CLASSES

Mar 14, 2022

Recommended Content

(20)

Test

Admission Of a Partner

class-2nd

Accountancy-Ii

0 Likes

26 Views

Kumar Nayak

Jan 22, 2022

Test

SARVOTTAM-YATI CLASSES ADMISSION TEST

class-2nd

Scholarshiptest

0 Likes

3 Views

Avinash

Jan 30, 2022

Test

Sarvottam-YATI CLASSES ADMISSION TEST

class-2nd

Scholarshiptest

0 Likes

2 Views

Avinash

Jan 30, 2022

Test

Sarvottam-YATI CLASSES ADMISSION TEST

class-2nd

Scholarshiptest

0 Likes

3 Views

Avinash

Jan 30, 2022

Test

Admission Test 2023

admissiontestahg

Test

0 Likes

8 Views

Abdul Hamid

Dec 14, 2021

Test

ABC CLASSES TEST

b-com

Ixth

0 Likes

13 Views

S.K. ATROULIYA

Nov 20, 2021

Test

Abhishiksha Classes

class-10th

Maths

1 Likes

7 Views

Abhishek Singh

Nov 21, 2021

Test

Admission

class-12th

Accountancy

0 Likes

24 Views

dawud khan

Nov 17, 2021

Test

Decent Classes

class-9th

Allsubjects

0 Likes

9 Views

Decent Classes

Nov 24, 2021

Test

Maths

class-2nd

Scholarshiptest

0 Likes

1 Views

Avinash

Jan 16, 2022

Test

Physics

class-2nd

Scholarshiptest

0 Likes

2 Views

Avinash

Jan 16, 2022

Test

Chemistry

class-2nd

Scholarshiptest

0 Likes

1 Views

Avinash

Jan 16, 2022

Test

Biology

class-2nd

Scholarshiptest

0 Likes

4 Views

Avinash

Jan 16, 2022

Test

Admission Test

class-7th

English

0 Likes

1 Views

J Bosco

Jan 12, 2022

Test

Integers, Fractions and Decimals and 7 others

class-7th

Scholarshiptest

0 Likes

1 Views

AYUSH RAJ

Apr 05, 2022

Homework

Coatching Classes

class-2nd

Coatchingclass

0 Likes

18 Views

Mohd Waseem

Jan 29, 2022

Test

admission

class-12th

Accountancy

0 Likes

9 Views

Rohan Seth

Oct 16, 2021

Test

Admission Test /(reward Test) /

class-6th

Allsubjects

0 Likes

32 Views

vikash sir

Dec 22, 2021

Test

Test For Partnerships Admission

class-12th

Accountancy

0 Likes

13 Views

PIYUSH BANSAL

Nov 17, 2021

Test

ONRA CLASSES

class-12th

Physics

0 Likes

13 Views

Mr. Adarsh Tiwari

Oct 24, 2021

Question Text

Question 1 :
Let a, b be non-zero real numbers. Which of the following statements about the quadratic equation $ax^2 + (a+b) x + b = 0$ is necessarily true? (I) It has at least one negative root. (II) It has at least one positive root. (III) Both its roots are real.

Question 2 :
The set of values of '$p$' for which the expression $x^2-2px+3p+4$ is negative for at least one real $x$ is-

Question 3 :
The value of k for which the roots are real and equal of the following equation $x^2$ - 4kx + k = 0 are k = 0, $\dfrac{1}{4}$

Question 4 :
Find the value of K so that sum of the roots of the equations $3x^2 + (2x - 11) x K - 5 = 0$ is equal to the product of the roots.

Question 5 :
If the equation $\displaystyle \lambda x^{2}-2x+3= 0$has positive roots for some real$\displaystyle \lambda $, then

Question 6 :
Statement 1 : Coefficient of ${ x }^{ 14 }$ in ${ \left( 1+2x+{ 3x }^{ 2 }\cdots +{ 16x }^{ 15 } \right) }^{ 2 }$ is 560 Statement 2 : $\sum _{ r=1 }^{ n }{ r(n-r)\quad =\quad \cfrac { n({ n }^{ 2 }-1) }{ 6 } } $

Question 7 :
If the $nth$ term of the AP $9, 7, 5..$ is same as the $nth$ term of the AP $15, 12, 9,...$, find $n.$

Question 8 :
Find the number of terms common to the two A,P's $3,7,11,.....,407$ and $2,9,16,..........,709$

Question 9 :
If in$\displaystyle \triangle ABC$ and$\displaystyle\triangle DEF$,$\displaystyle \frac{AB}{DE}=\frac{BC}{FD}$ then they will be similar if

Question 10 :
In quadrilateral ABCD, the diagonals AC and BD intersect each at point O. If $AO=2CO$ and $BO=2DO$; Then,$\displaystyle \Delta AOB$ is similar to $\displaystyle \Delta COD$

Question 11 :
In $\triangle ABC \sim \triangle DEF$ such that $AB = 1.2\ cm$ and $DE = 1.4\ cm$. Find the ratio of areas of $\triangle ABC$ and $\triangle DEF$.

Question 12 :
D and F are mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E. Find AB (in cm), if EF = 4.8 cm.

Question 13 :
If HCF of numbers $408$ and $1032$ can be expressed in the form of $1032x -408 \times 5$, then find the value of $x$.

Question 14 :
If $x=6+2\sqrt {6}$, then what is the value of $\sqrt { x-1 } +\cfrac { 1 }{ \sqrt { x-1 } } $?

More from YATI CLASSES

Recommended Content

Learn from Anywhere on Any Device