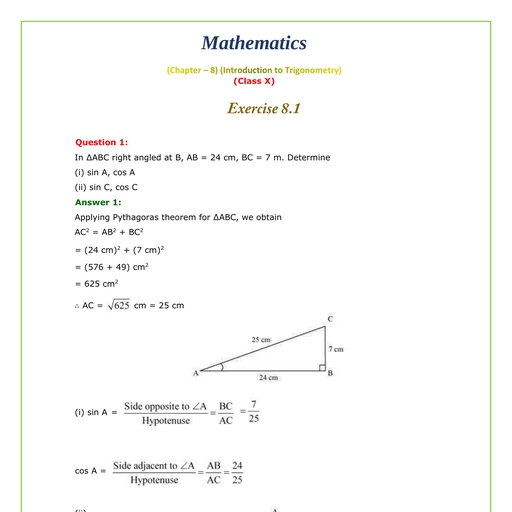
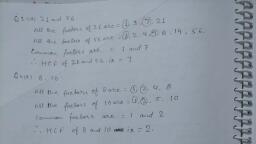Question 1 :
<u></u>The number of ordered pairs $(a, b)$ of positive integers, such that $a + b = 90$ and their greatest common division is $6$, equals
Question 5 :
If two positive integers $a$ and $b$ are written as $a = x^3y^2$ and $b = xy^3$; $x, y$ are prime numbers, then $ HCF (a, b)$ is<br>
Question 6 :
Deepika has more than $30$ stickers but less than $40$ stickers. She can pack the stickers into packs of $2, 3$ or $4$ without leaving any remainder. How many stickers does she have?
Question 8 :
If product of two numbers is 32 and L.C.M. is 8, then its H.C.F. is ________.
Question 9 :
The LCM of two numbers is x and their HCF is y. The product of two numbers is<br>
Question 10 :
If the HCF of 48 and 80 is 16, find their LCM
Question 11 :
Four bells ring at intervals of $4, 6, 8$ and $14$ seconds. They start ringing simultaneously at $12.00$ O'clock. At what time will they again ring simultaneously?
Question 14 :
Given that H.C.F. $(306, 1314) = 18,$ find LC.M. $(306, 1314)$.
Question 15 :
Choose the correct answer form the alternatives given.<span><br>What is the HCF of $(x^4 \, - \, x^2 \, - \, 6) \, and \, (x^4 \, - \, 4x^2 \, + \, 3)$? </span>
Question 17 :
Which greatest number of 4-digits is exactly divisible by $12, 15,20 \ and \ 35 $ ?<br/>
Question 19 :
The average of three numbers is $40$. The first number is twice the second and the second one is thrice the third number. The difference between the largest and the smallest numbers is
Question 20 :
The HCF of two expressions p and q is 1. Their LCM is
Question 21 :
If $H.C.F$ of two numbers $306$ and $657$ is $9$, then find their $L.C.M$.
Question 23 :
The HCF of two number is 28 and their LCM is 336 If one number is 112 then the other number is
Question 24 :
Two ropes $16m$ and $20m$ long are to be cut into small pieces of equal lengths. What will be the maximum length of each piece?
Question 25 :
The HCF of two numbers is $28$ and their LCM is $336$. If one number is $112$, then the other number is _________.
Question 26 :
Four bells ring at intervals of 6, 7, 8 and 9 seconds respectively. All the bells ring together after ............ seconds
Question 27 :
HCF of 3240, 3600 and a third number is 36 and their LCM is $\displaystyle 2^{4}\times 3^{5}\times 5^{2}\times 7^{2}$ Then the third number is
Question 28 :
Bhushan counted to $60$ using multiples of $6.$ Which statement is true about multiples of $6?$<br/>
Question 29 :
The least multiple of $7$, which leaves the remainder $4$, when divided by any of $6, 9, 15$ and $18$ is
Question 30 :
Six bells commence tolling together and toll at intervals of $2$, $4$, $6$, $8$, $10$ and $12$ seconds respectively. In $30$ minutes, how many times do they toll together?
Question 34 :
The HCF of two number is $28$ and their LCM is $336$. If one number is $112$ then, the other number is<br/>
Question 35 :
The LCM of two numbers is $2079$ and their HCF is $27$. If the first number is $189$, then the second number is
Question 36 :
The sum of L.C.M. and H.C.F. of two numbers is 1260. If their L.C.M. is 900 more than their H.C.F., find the product of two numbers.
Question 37 :
The H.C.F. and L.C.M. of two numbers are 84 and 21 respectively. If the ratio of the two numbers is 1:4, then the large of tthe two numbers is ;
Question 38 :
If the  two numbers are  $396$ and  $576$ and the L.C.M. is $6336$. Their G.C.D. is
Question 39 :
How many numbers less than $1000$ are multiples of both $10$ and $13$?
Question 40 :
If the HCF of 85 and 153 is expressible in the form $85n -153$, then the value of n is:<br/>
Question 41 :
What is the smallest number which when increased by $3$ is divisible by $27, 35, 25$ and $21$?
Question 42 :
P is the LCM of 2,4,6,8,10, Q is the LCM of 1,3,5,7,9 and L is the LCM of P and Q. Then, which of the following is true ?<br/>
Question 43 :
The L.C.M. of two numbers is $(a + b)$ and their H.C.F. is $k(a - b)$. If one of the numbers is k, find the other number
Question 44 :
What is the smallest positive integer which when divided by $4, 5, 8, 9$ leaves remainders $3, 4, 7, 8$ respectively?
Question 45 :
A certain type of wooden board is sold only in lengths of multiples of $25$ cm from $2\  to \ 10$ meters. A carpenter needs a large quantity of this type of board in  $1.65$ m length. For the minimum waste, the length to be purchased should be
Question 46 :
$x$ is twice the difference between the $6$th and $10$th multiple of $7$. Find the value of $x$.
Question 47 :
Find the largest positive integer that will divide $122, 150, $ and $115$ leaving remainder $5, 7$ and $11$ respectively.
Question 48 :
Which of the following is NOT a positive multiple of 12?
Question 49 :
There is a circular path around a sports field. A takes 18 minutes to drive one round of the field, while B takes 12 minutes for the same direction, after how many minutes will they meet again at the starting point.<br/>
Question 50 :
Find the least number which when divided by $20, 18$ and $30$ gives the same remainder $9$ in each case.
Question 51 :
Write the least $2$ digit number that has $2, 5$ and $8$ as factors.
Question 52 :
Three bells ring at intervals of 36 seconds, 40 seconds and 48 seconds respectively. If they ring together now, then how many minutes later they ring together again?<br/>
Question 54 :
If the sum of two numbers is $55$ and H.C.F. and L.C.M. of these numbers are $5$ and $120$ respectively, then what is the sum of the reciprocals of these numbers?
Question 55 :
If the students of a class can be grouped exactly into $6, 8$ or $10,$ then what is the minimum number of students in the class?
Question 56 :
The largest number that divides $2053$ and $967$ and leaves a remainder of $5$ and $7$ respectively is<br/>
Question 57 :
Match the following.<br><table class="wysiwyg-table"><tbody><tr><td></td><td>Column I</td><td></td><td>Column II</td></tr><tr><td>(i)</td><td>49</td><td>(p)</td><td>Multiple of 3</td></tr><tr><td>(ii)</td><td>25</td><td>(q)</td><td>Multiple of 4</td></tr><tr><td>(iii)</td><td>16</td><td>(r)</td><td>Multiple of 7</td></tr><tr><td>(iv)</td><td>39</td><td>(s)</td><td>Multiple of 5</td></tr></tbody></table>(i) (ii) (iii) (iv)
Question 58 :
If $a$ and $b$ are any two positive integers then $ \mathrm{HCF}(\mathrm{a}, \mathrm{b}) \times \mathrm{LCM}(\mathrm{a}, \mathrm{b}) $ is equal to
Question 59 :
Mark the correct alternative of the following.<br>The HCF of two co-primes is?<br>
Question 60 :
Find the least number which when divided by 35 leaves a remainder 25, when divided by 45 leaves a remainder 35 and when divided by 55 leaves a remainder 45.
Question 61 :
If the LCM of  $\displaystyle \left ( x^{2}+3x \right )\left ( x^{2}+3x+2 \right )$ and  $\displaystyle \left ( x^{2}+6x+8 \right )\left ( x^{2} + kx + 6 \right )$ is  $\displaystyle x \left ( x+1 \right )\left ( x+2 \right )^{2}\left ( x+3 \right )\left ( x+4 \right )$ then find $k$.
Question 62 :
If HCF and LCM of two numbers are $6$ and $60$ respectively, then those numbers are
Question 63 :
What is the greatest number that exactly divides $105, 1001$ and $2436$?
Question 64 :
The LCM and HCF of two given numbers are $960$ and $8$ respectively. If one of them is $64,$ then the other number is
Question 65 :
If H.C.F. of 210 and 55 is expressed in the form of 210 $\times$ 5 + 55y, find the value of $y^2$.
Question 67 :
Three numbers are in the ratio 2:3:4 and their HCF is 12. The LCM of the numbers is:
Question 68 :
The ratio of the sum to the LCM of two natural numbers is $7:12$. If their HCF is $4$, then the smaller number is
Question 69 :
Which greatest possible length can be used to measure exactly $15 \ m$ $75 \ cm,11 \ m$ $25 \ cm$ and $7 \ m$ $65 \ cm$?
Question 70 :
Seema, Meena and Reema begin to jog around a circular stadium and they complete their revolution in $54$ seconds , $42$ seconds and $63$ seconds respectively. After approximately how many minutes will they come together at the starting point ?