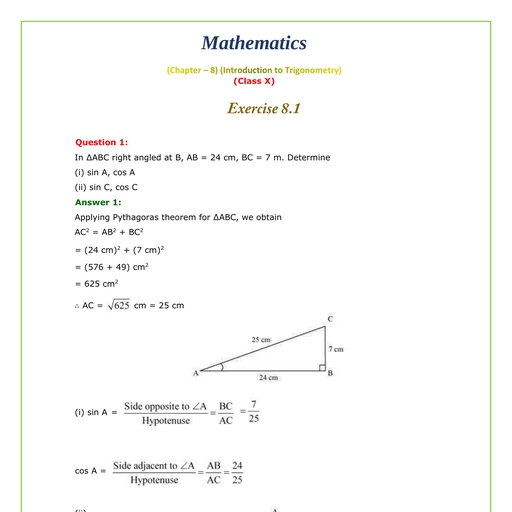
Question 1 :
In a right angled triangle one angle is $\displaystyle 48^{\circ}$. Then the remaining angle is:
Question 2 :
An obtuse triangle will have one and only one _______ angle.<br>
Question 3 :
The largest angle of a triangle, if the ratios of its angles are $2:3:4$, is:
Question 4 :
The centroid of the triangle whose vertices are (4,-8) ,(-9,7) and (8,13) is
Question 5 :
A ______ triangle is a triangle with one angle that is exactly $90^{o}.$<br/>
Question 7 :
In a triangle, there are 3 different angles. Which of the following statements is/are definitely true about the angles?<br>(i) Sum of all the angles is $100^o$.<br>(ii) One angle is obtuse and other two are acute and right angle respectively. <span><br>(iii) Sum of any two angles is always less than $180^o$. </span>
Question 8 :
In triangle $ABC, \angle A= \angle B=52^o$, write the name of its largest side.
Question 9 :
A triangle that has an angle greater than ____  is called as obtuse triangle.<br/>
Question 11 :
Which of the following can't be a angle of the right angled triangle?
Question 12 :
In a traingle ABC<div>Given : $\angle A=9x-15^o; \angle B=4x\,\, and \,\, \angle C=3x + 15^o$. Calculate $\angle B$</div>
Question 14 :
Write the measure of each angle of an isosceles right-angled triangle.
Question 15 :
In a $\triangle ABC$, $\angle C = 3 \angle B = 2 (\angle A + \angle B)$. The three angles will be _________.
Question 16 :
In $\displaystyle \Delta PQR$, if $\displaystyle \angle R={ 90 }^{ o }$, then angles P and Q are
Question 17 :
An exterior angle of a triangle is $105^o$ and its two interior opposite angles are equal. Each of these equal angles is:<br/>
Question 18 :
If angles of triangle are in a ratio 1:1:2.measures of all the angles will be?
Question 19 :
In triangle $ABC, \angle C=120^o$, write the name of the its largest side.
Question 20 :
The ${\triangle }$ formed by BC =7.2 cm , AC =6 cm and ${\angle C}$ = ${120^0}$ is:
Question 21 :
If D is any point on the side BC of $\Delta ABC$ such that $\Delta ADB$ and $\Delta ADC$ are equal in area, then<br/>
Question 22 :
One of the angles of a triangle is $75^{\circ}$. If the difference of the other two angles is $35^{\circ}$, then the largest angle of the triangle has a measure of :<br/>
Question 23 :
An exterior angle of a triangle is $80^{\circ}$ and two interior opposite angles are equal. Measure of each of these angle is :<br/>
Question 24 :
In a triangle ABC, $\angle A = 80^o$ and $AB = AC$, then $\angle B$ is ....................
Question 25 :
ABC is a triangle and AD is median. If E is any point on AD, then<br>
Question 26 :
If two angles of a triangle are $60^o$ each, then the triangle is
Question 28 :
In $\Delta ABC, \angle A = \dfrac{\angle B}{2} = \dfrac{\angle C}{6}$. Then the measure of A is :<br/>
Question 30 :
If the largest angle in a triangle is $80^{\circ}$, then the least possible integral value of smallest angle of the triangle is
Question 31 :
If the angles of $\Delta$ le are in the ratio $1 : 2 : 7$, then the $\Delta$ le is
Question 32 :
In a triangle, there are 3 different angles. Which of the following statements is/are definitely true about the angles?<br>(i) Sum of all the angles is $100^o$.<br>(ii) One angle is obtuse and other two are acute and right angle respectively. <span><br>(iii) Sum of any two angles is always less than $180^o$. </span>
Question 33 :
The sides of a right triangle are $9,12$ and $15$ cm long. Find the sum of the squares of the medians. 
Question 34 :
If two angles in a triangle are $65^{\circ}$ and $85^{\circ}$, then the third angle is:
Question 35 :
In $\Delta ABC$, $ \angle A = \angle B/2 = \angle C/6$. Then the measure of $\angle A$ is:<br>
Question 36 :
The point O lies inside a triangle PQR such that $\Delta OPQ,\Delta OQR $ and $\Delta ORP$, are equal in area. Then,the point O is called as <br>
Question 38 :
Of the following sets of data the only one that does not determine the area of a triangle is:
Question 40 :
In $\Delta PQR $ <p=2 <Q and 2 < R=3 < Q, Calculate the angles of $\Delta PQR$.<br/><br/>
Question 41 :
In a $\displaystyle \Delta ABC, \ AB=AC=2.5cm, \ BC=4cm.$ Find its height from $A$ to the opposite base.
Question 43 :
Origin is the centre of circle passing through the vertices of an equilateral triangle whose median is of length $3a$ then equation of the circle is?
Question 44 :
In $ \Delta ABC$, $\angle A-\angle B = 16$ and $\angle C - \angle A = 34$;  find all the angles of the triangle.
Question 45 :
The vertex angle of an isosceles triangle measures $84^{o}.$ What is the measure of base angle<br/>
Question 47 :
Vertices of a $\bigtriangleup$ABC are A (2, 2), B (-4, -4)and C (5, -8), then the length of the median through C is :
Question 48 :
The three angles of a triangle have measures of $x^o$, $2x^o$, and $y^o$, where $x$ $ > 55^o$. If $x$ and $y$ are integers, what is one possible value of $y$?
Question 49 :
If each side of an equilateral triangle is $8$, calculate the length of the altitude.
Question 50 :
In a $\displaystyle \Delta ABC,AD\perp  {BC}$ and $\displaystyle {CF}\perp {AB},AB = 6.4 $ $cm$, $CF = 2.6\ cm$, $AD = 3.2\ cm$. Find the (in $cm$) length of the side $BC$ (in $cm$).<br/>
Question 51 :
Which of the following will form a right angled triangle, given that the two angles are:
Question 52 :
The first of a triangle is one-third its second angle, whereas the third angle is $5$ times the first angle. Find the measure of all the angles of the triangle.
Question 54 :
If each side of an equilateral triangle is doubled then its angle will ______
Question 55 :
If two sides of an isosceles triangle are 4 cm and 10 cm then the length of the third side is__
Question 57 :
In a triangle $ABC$, the sides are of length $17,\ 25$ and $28$ units. Then, the length of the largest altitude is
Question 58 :
An isosceles triangle contains three angles that measure $40^{\circ}, x^{\circ}$, and $y^{\circ}$. Which of the following CANNOT be true?
Question 59 :
The angles of the triangles ABC and DEF are given as follows :<br>$A=90^0,B=30^0,D=90^0 and E=30^0.$<br><br>If the side BC is twice the side EF, then<br><br>
Question 60 :
The mean of 10 observations is 16.3. If one observation is registered as 32 instead of 23, then new mean is<br>
Question 61 :
Vertical angles of two isosceles triangles are equal. If their areas are in the ratio $16:25$, then find the ratio of their altitudes drawn from vertex to the opposite side.
Question 62 :
An isosceles triangle with base $24$ and legs of $15$ is inscribed in a circle. Find the radius.
Question 63 :
A triangle with one right angle and two acute angles is called _______ angled triangle.
Question 64 :
In an equilateral triangle if 3 times the square of one side is equal to K times the square of its altitude then K equals
Question 65 :
If in an equilateral triangle with side a, then the alt