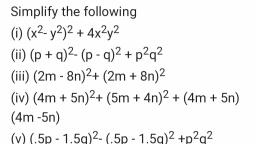Question 1 :
If Leah is $6$ years older than Sue and John is $5$ years older than Leah and the total of their ages is $41$. Then how old is Sue?

Question 2 :
A Gym sells two types of memberships. One packages costs $ $325$ for one year of membership with an unlimited number of visits. The second package has a $ $125$ enrolment fee, includes five free visits, and costs an additional $ $8$ per visit after first five. How many visits would a person need to use for each type of membership to cost the same amount over a one-year period?

Question 3 :
A diagonal of a rectangle is inclined to one side of the rectangle at $25^o$. Find the acute angle between the diagonals.

Question 4 :
Given that $Q$ is a rational number:(i) Difference of two $Q$s is $Q$.(ii) Subtraction is commutative on $Q$.(iii) Addition is not commutative on $Q$.Which option is wrong?

Question 5 :
While representing $\dfrac23$ on a number line, between which $2$ integers does the point lie?

Question 6 :
$G$ is a set of all rational numbers except $-1$ and $\ast $ is defined by $a\ast b=a+b+ab$ for all $a,b\in G$, in the group $\left( G,\ast \right) $, the solution of ${ 2 }^{ -1 }\ast x\ast { 3 }^{ -1 }=5$ is

Question 7 :
A computer is programmed to add $3$ to the number $N$, multiply the result by $3$, subtract $3$, and divide this result by $3$. The computer answer will be

Question 8 :
Arrange the following steps in correct order in constructing a square whose one diagonal is $5$cm.<br/>Step 1 : Let PQ cut AC at O.<br/>Step 2 : Draw a diagonal AC = $5$cm.<br/>Step 3 : Join Ab, BC, CD and DA. Then ABCD is the required square.<br/>Step 4 : Draw PQ the perpendicular bisector of AC.<br/>Step 5 : With O as centre and OA radius draw a circle. Let the circle cut QP at points B and D.<br/>

Question 10 :
Find the square root of $8100$ by the prime factorisation method.<br/>

Question 11 :
If x is a positive integer less than 100, then the number of x which make&#160;$\displaystyle \sqrt{1+2+3+4+x}$ an integer is

Question 12 :
A coin is tossed $100$ times and tail is obtained $10$ times. Now, if a coin is tossed at random, what is the probability of getting a head?<br/>

Question 13 :
$20$ card are numbered from $1$ to $20$. One card is drawn at random. What is the probability that the number on the card is greater than $12$?

Question 14 :
The following table gives the monthly expenditure of two families:<table class="wysiwyg-table"><tbody><tr><td></td><td>Expenditure (in Rs.)</td><td>Expenditure (in Rs.)</td></tr><tr><td>Items</td><td>Family $A$</td><td>Family $B$</td></tr><tr><td>Food</td><td>$3,500$</td><td>$2,700$</td></tr><tr><td>Clothing</td><td>$500$</td><td>$800$</td></tr><tr><td>Rent</td><td>$1,500$</td><td>$1,000$</td></tr><tr><td>Education</td><td>$2,000$</td><td>$1,800$</td></tr><tr><td>Miscellaneuous</td><td>$2,500$</td><td>$1,800$</td></tr></tbody></table>In constructing a pie diagram to the above data, the radii of the circles are to be chosen by which one of the following ratios?

Question 15 :
Find the value of cube root of the number $45$. (Round off your number to the nearest whole number)<br/>

Question 16 :
Choose the correct answer from the alternatives given.<br>If $x \, = \, 2^{\frac{1}{3}} \, + \,2^{\frac{-1}{3}}$ then the value of $2x^3 \, - \, 6x$ will be

Question 17 :
Given that $1{cm}^{3}$ of a metal weighs $5gms$, the weight of a cylindrical metal container with base radius $20.5cm$ and height $60cm$ is:

Question 18 :
Find (x, y) if (3, 2), (6, 3), (x, y) and (6, 5) are the vertices of a parallelogram.

Question 19 :
Let $n&gt; 1$ be an integer. Which of the following sets of numbers necessarily contains a multiple of $3$?

Question 20 :
If A = $10{w}^{3} + 20{w}^{2} - 55w + 60$,<br>B = $-25{w}^{2} + 15w - 10$ and<br>C = $5{w}^{2} - 10w + 20$,<br>then A + B - C is equal to ______.

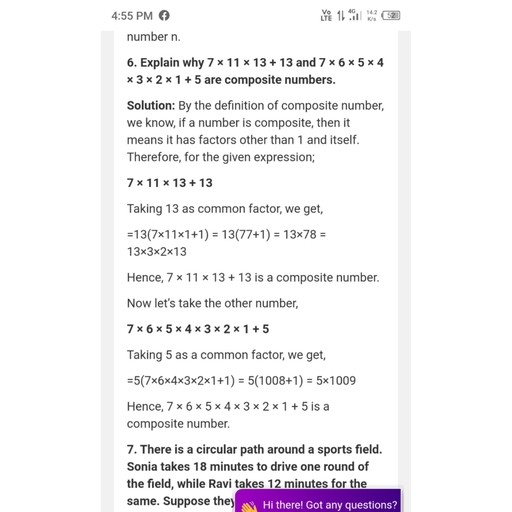
Question 23 :
Two numbers are such that their sum multiplied by the sum of their squares is $5500$ and their difference multiplied by the difference of the squares is $352$. Then the numbers are ?<br/>

Question 24 :
Simplify: $\displaystyle 18xy\left( 16{ x }^{ 2 }-25{ y }^{ 2 } \right) \div 3xy\left( 4x+5y \right)&#160;$

Question 27 :
What will be the product of first monomial $-4xy$ and second monomial $-4xy$ ?

Question 28 :
Which of the following will have 4 at the units place?

Question 29 :
The square root of a number x is the number whose square is

Question 30 :
For a given job, more the number of workers, ______ will be the time taken to complete the work.