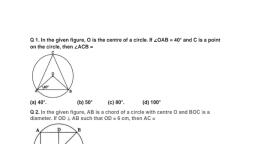
Question 2 :
The abscissa of two points A and B are the roots of the equation ${x^2} + 2ax - {b^2}$ and their ordinates are the root of the equation ${x^2} + 2px - {q^2}=0$. the equation of the circle with AB as diameter is 

Question 3 :
The points $A\left( {2a,\,4a} \right),\,B\left( {2a,\,6a} \right)\,$ and $C\left( {2a + \sqrt 3 a,\,5a} \right)$ (when $a>0$) are vertices of 

Question 4 :
If the coordinates of the extermities of diagonal of a square are $(2,-1)$ and $(6,2)$, then the coordinates of extremities of other diagonal are

Question 5 :
A polynomial when divided by $\displaystyle \left ( x-6 \right )$ gives a quotient $\displaystyle x^{2}+2x-13$ and leaves a remainder $-8$. Then polynomial is

Question 6 :
If $a = \dfrac{3 +\sqrt{5}}{2}$, then find the value of $a^{2} +\dfrac{1}{a^{2}}$.

Question 8 :
Which of the following is the remainder when $z\left({5z}^{2}-80\right)$ is divided by $5z\left(z-4\right)$:

Question 9 :
The angles between the lines $3 x + y - 7 = 0 \text { and } x + 2 y + 9 = 0$ is:

Question 10 :
Reduce equations to a pair of linear equations and find the value of&#160;x and y: <br/>$\dfrac{6}{x} + \dfrac{1}{y} = 31; \dfrac{2}{x} + \dfrac{3}{y} = 16$

Question 11 :
$300$ works were engeged to finish a piece of work in a certain number pf days. $8$ workers dropped on the second day, $8$ more workersdropped the third day and so on. It takes $8$ more days to finish the work now. Find the number of days in which the work was completed.

Question 12 :
Total cost of $15$ erasers and $25$ pencils is Rs. $185$ and the total cost of $9$ erasers and $x$ pencils is Rs. $106$. Which of the following cannot be the value of $x$?

Question 14 :
Two distinct ________ lines cannot be parallel to the same line.<br/>

Question 15 :
Select the correct answer. The three steps from solids to point are

Question 16 :
If ${n}^{k}=64$ and $n$ and $k$ are integers, which of the&#160;following cannot be a value of $n$?

Question 18 :
A computer is programmed to add $3$ to the number $N$, multiply the result by $3$, subtract $3$, and divide&#160;this result by $3$. The computer answer will be

Question 19 :
What is the value of $a$ and $b$, if $\sqrt{25x^2+50x^3+35x^2+ax+b}$ is a perfect square?<br/>

Question 20 :
A line is divided into three parts. The first part is two third the length of the second part. The third part is&#160;$\displaystyle \frac{1}{2}cm $ shorter than the first part and $2\ cm$ shorter than the second part. Find the length of the line?

Question 21 :
The measure of an angle which is four times its supplementary angle is:<br/>

Question 22 :
Out of $100$ numbers $20$ were $5s$, $30$ were $6s$ and the remaining were $7s$. The arithmetic mean of the numbers is

Question 23 :
The mean of 50 observations is 36. If its twoobservations 30 and 42 are deleted, then the meanof the remaining observations is

Question 24 :
The captain of a cricket team of 11 members is 26 years old and the wicketkeeper is 3 years older than the captain. If the ages of these two are excluded, the average age of the remaining players is one year less than the whole team. What is the average age of the team?

Question 25 :
If the first and the second letters of the word MISJUDGEMENTS are interchanged with the last and the second last letters respectively, and similarly the third and the fourth letters are interchanged with the third and the fourth letters from the last respectively , and so on,then what will be the fifth letter to the right of the third letter from the left end?