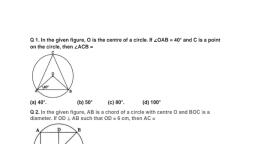
Question 1 :
If ${x_1},{x_2},{x_3}$ as well as ${y_1},{y_2},{y_3}$ are in&#160;<b>G.P.&#160;</b> with same common ratio, then the points&#160;<b></b>$P\left( {{x_1},{y_1}} \right)$, $Q\left( {{x_2},{y_2}} \right)$&#160;and $R\left( {{x_3},{y_3}} \right)$&#160;

Question 2 :
A line has the equation $x =-2y +z$. If $(3, 2)$ is a point on the line, what is $z$?

Question 3 :
If the coordinates of the extermities of diagonal of a square are $(2,-1)$ and $(6,2)$, then the coordinates of extremities of other diagonal are

Question 4 :
The points $A\left( {2a,\,4a} \right),\,B\left( {2a,\,6a} \right)\,$ and $C\left( {2a + \sqrt 3 a,\,5a} \right)$ (when $a&gt;0$) are vertices of&#160;

Question 7 :
State whether the following statement is True or False<br>The conjugate of $\sqrt {3} + \sqrt {2}$ is $\sqrt {2} - \sqrt {3}$

Question 10 :
Use the identity $(x + a) (x + b) = x^2 + (a + b) x + ab$ to find the given product.<br/>Multiply $(x + 3) (x + 7).$

Question 12 :
If a remainder of $4$ is obtained when $x^{3} + 2x^{2} - x - k$ is divided by $x - 2$, find the value of $k$.

Question 15 :
Reduce equations to a pair of linear equations and find the value of&#160;x and y: <br/>$\dfrac{6}{x} + \dfrac{1}{y} = 31; \dfrac{2}{x} + \dfrac{3}{y} = 16$

Question 16 :
Twice a number minus three times another is equal to $2$. The sum of these numbers is $11$. The difference of these numbers is

Question 17 :
Ravi distributed the chocolates with him equally between Rajesh and Suresh. He was left with a chocolate. Rajesh distributed his share equally among three of his friends and was also left with a chocolate. One of the three distributed his share equally among four of his friends and was left with no chocolate. Which of the following could be the number of chocolates that Rajesh received?

Question 19 :
Find smallest of&#160;two supplementary angles, if they are in the ratio $7 : 11$.

Question 21 :
I. If the points $(\mathrm{a},0)$ , $(\mathrm{b},0)$ , $(0,\mathrm{c})$ , $(0,\mathrm{d})$ are concyclic, then $ab=cd$<br/>II. If the points $(1,-6) , (5,2), (7,0), (-1, \mathrm{k})$ are concyclic then $\mathrm{k}=-3$.<br/>

Question 22 :
If two lines $\displaystyle \displaystyle a_{1}x+b_{1}y+c_{1}=0$ and $\displaystyle a_{2}x+b_{2}y+c_{2}=0$ cut the coordinate axes in concyclic points,then <br>

Question 23 :
The construction of $\Delta EFG$ when $FG=3$ $cm$ and m$\angle G=60^\circ$ is possible when difference of $EF$ and $EG$ is equal to:

Question 25 :
The construction of $\Delta LMN$ when $MN=6$ $cm$ and $m\angle M=45^\circ$ is not possible when difference between $LM$ and $LN$ is equal to:

Question 26 :
If each of 'n' readings are increased by 5, then the arithmetic mean of new 'n' readings is equal to 10. If each of the original readings are multiplied by 3, then the arithmetic mean of new readings will be

Question 27 :
Mean of twenty observations is 15. If two observations 3 and 14 are replaced by 8 and 9 respectively, then the new mean will be<br>

Question 28 :
If the ratio of mean and median of a certain data is $5:7$, then find the ratio of its mode and mean.

Question 29 :
The captain of a cricket team of 11 members is 26 years old and the wicketkeeper is 3 years older than the captain. If the ages of these two are excluded, the average age of the remaining players is one year less than the whole team. What is the average age of the team?