Test Details

Math Class 9th Test

Dec 30, 5:05 PM

30 minutes

Dec 30, 5:35 PM

64.0 marks

MCQ

30 questions

Mayur Sir

Mayur Raj has completed B. Tech from Electrical Engineering and Now Pursuing BA- LLB . He is teaching from 2013 Now He has transformed teaching section for students or parents that deserve education.

Class Details

All

Class 9th

All

इस Class,में Class 9th के Math, Science, Sst, Hindi Literature, English Literature जैसे सभी विषय की जानकारी दिए जाएंगे।

More from Mayur Sir

(20)

Test

Introduction to Trigonometry

class-10th

All

0 Likes

11 Views

Mayur Sir

Oct 29, 2022

Test

Force and Pressure, Sound and 1 others

class-8th

All

0 Likes

3 Views

Mayur Sir

Oct 29, 2022

Lecture

Lecture 2022-06-23

class-9th

All

0 Likes

2 Views

Mayur Sir

Jun 23, 2022

Lecture

Lecture 2022-06-23

class-9th

All

0 Likes

2 Views

Mayur Sir

Jun 23, 2022

Lecture

Lecture 2022-06-23

class-9th

All

0 Likes

5 Views

Mayur Sir

Jun 23, 2022

Lecture

Lecture 2022-04-30

class-10th

All

0 Likes

14 Views

Mayur Sir

Apr 30, 2022

Lecture

Class 7th Math Ncert

class-7th

All

1 Likes

19 Views

Mayur Sir

Apr 20, 2022

Lecture

Components Of Food

class-6th

All

1 Likes

22 Views

Mayur Sir

Apr 19, 2022

Lecture

Chemical Reaction & Eqn

class-10th

All

0 Likes

8 Views

Mayur Sir

Apr 19, 2022

Study Material

Lecture 19-Apr-2022.pdf

class-10th

All

0 Likes

7 Views

Mayur Sir

Apr 19, 2022

Study Material

Lecture 18-Apr-2022.pdf

class-10th

All

0 Likes

6 Views

Mayur Sir

Apr 18, 2022

Lecture

Understanding Diversity

class-6th

All

0 Likes

7 Views

Mayur Sir

Apr 15, 2022

Study Material

शिक्षा का अधिकार.pdf

b-com

All

1 Likes

560 Views

Mayur Sir

Mar 24, 2022

Test

Force and Laws of Motion, Sound and 3 other Topics

class-12th

Allsubjects

0 Likes

8 Views

Mayur Sir

Mar 03, 2022

Test

Force and Pressure, Chemical Effects of Electric Current and 5 other Topics

class-12th

Allsubjects

0 Likes

10 Views

Mayur Sir

Mar 03, 2022

Test

Understanding Quadrilaterals, Comparing Quantities and 4 other Topics

जनकआदत

अनकनक

0 Likes

12 Views

Mayur Sir

Mar 03, 2022

Test

Chemical Kinetics,Surface Chemistry

class-12th

Allsubjects

0 Likes

4 Views

Mayur Sir

Mar 02, 2022

Test

Chemical Kinetics,Surface Chemistry

class-12th

Allsubjects

0 Likes

3 Views

Mayur Sir

Mar 02, 2022

Test

Areas of Parallelograms and Triangles, Circles and 5 other Topics

जनकआदत

अनकनक

0 Likes

10 Views

Mayur Sir

Mar 02, 2022

Test

Number Systems, Polynomials and 4 other Topics

b-com

All

0 Likes

0 Views

Mayur Sir

Mar 02, 2022

Recommended Content

(20)

Test

Class 9th Chemistry Test

class-9th

All

0 Likes

34 Views

Mayur Sir

Dec 08, 2021

Test

Class 7th Test Math

class-7th

All

0 Likes

7 Views

Mayur Sir

Dec 11, 2021

Test

Class 9th Math Test

class-9th

All

0 Likes

15 Views

Mayur Sir

Dec 11, 2021

Test

Class 9th Test Math

class-9th

All

0 Likes

12 Views

Mayur Sir

Dec 11, 2021

Test

Class 9th Test Math

class-9th

All

0 Likes

20 Views

Mayur Sir

Dec 12, 2021

Test

Class 9th Math Test Revision Syllabus

class-9th

All

0 Likes

6 Views

Mayur Sir

Dec 08, 2021

Test

Class 5th Math Test

class-5th

All

0 Likes

13 Views

Mayur Sir

Dec 30, 2021

Test

Class 9th test

class-9th

Socialscience

0 Likes

5 Views

Pawan

Jan 24, 2022

Test

Class 9th Test

class-9th

Maths

0 Likes

27 Views

GOLDY NARANG

Jan 24, 2022

Test

Class 10th Math Test

class-10th

All

0 Likes

12 Views

Mayur Sir

Dec 12, 2021

Test

Class 9th Science Test

class-9th

Mathematics

0 Likes

5 Views

Sandeep Singh

Mar 05, 2022

Test

Class 5th Math Test

class-5th

All

0 Likes

12 Views

Mayur Sir

Dec 30, 2021

Test

Class 11th Math Test

class-11th

All

0 Likes

13 Views

Mayur Sir

Dec 08, 2021

Test

Class 6th Math Test

class-6th

All

0 Likes

8 Views

Mayur Sir

Dec 30, 2021

Test

Class 8th Math Test

class-8th

All

0 Likes

9 Views

Mayur Sir

Dec 11, 2021

Test

Class 8th Math Test

class-8th

All

0 Likes

6 Views

Mayur Sir

Dec 30, 2021

Test

Class 6th Math Test

class-6th

All

0 Likes

13 Views

Mayur Sir

Dec 08, 2021

Test

Class 6th Math Test

class-6th

All

0 Likes

10 Views

Mayur Sir

Dec 30, 2021

Test

Class 8th Math Test

class-8th

All

0 Likes

14 Views

Mayur Sir

Dec 30, 2021

Test

Class 5th Math Test

class-5th

All

0 Likes

11 Views

Mayur Sir

Dec 30, 2021

Question Text

Question 1 :
Find out whether or not the first polynomial is a factor of the second polynomial $x-3, x^3+4x^2-3x+5$

Question 3 :
Square root of $\dfrac {x^{2}}{y^{2}} + \dfrac {y^{2}}{4x^{2}} - \dfrac {x}{y} + \dfrac {y}{2x} - \dfrac {3}{4}$ is $\dfrac {x}{y} - \dfrac {1}{2} - \dfrac {y}{2x}$

Question 4 :
Simplify: $\displaystyle \frac { 49\left( { x }^{ 4 }-2{ x }^{ 3 }-15{ x }^{ 2 } \right)  }{ 14x\left( x-5 \right)  } $

Question 6 :
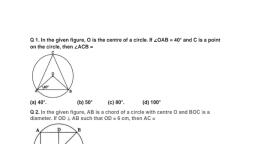
Two distinct ________ lines cannot be parallel to the same line.

Question 8 :
 Two supplementary angles are in the ratio $3:2$. The smaller angle measures?

Question 9 :
After covering a distance of $30\ km$ with a uniform speed there is some defect in a train engine and therefore its speed is reduced to $\dfrac{4}{5}$ of its original speed. Consequently the train reaches its destination late by $45$ minutes. Had it happened after covering $18$ kilometers more the train would have reached $9$ minutes earlier, find the speed of the train and the distance of journey.

Question 10 :
Find the value of $k$ for which the following system of linear equation becomes infinitely many solution or represent the coincident lines. $6x+3y=k-3$; $2kx+6y=k$

Question 11 :
The budget for the annual day function of a school was Rs. $60,000$, out of which Rs. $14,500$ was paid to the tent house, Rs. $10,400$ to the band party and Rs. $5,000$ for refreshments. How much money was left over after meeting the expenses?

Question 12 :
The cost of using a telephone in a hotel meeting room is $ $0.20$ per minute. Which of the following equations represents the total cost $c$, in dollars, for $h$ hours of phone use?

Question 13 :
If a $\triangle PQR$ is constructed taking QR = $5$ cm, PQ = $3$ cm and PR = $4$ cm, then the correct order of the angles of the triangle is:

Question 14 :
In $\triangle ABC$ and $\triangle PQR$, $\angle A = \angle Q$ and $\angle B = \angle R.$ Which side of $\Delta$ $PQR$ should be equal to side $AB$ of $\Delta ABC$ so that the two triangles are congruent?

Question 15 :
Given that ABCD is a parallelogram. If AC is perpendicular to BD but is not equal to it then ABCD is a Rhombus.

Question 16 :
Find the midpoint of the segment connecting the points $(a, -b)$ and $(5a, 7b)$.

Question 17 :
Two adjacent angles of a parallelogram are $(2x + 30)^{\circ}$ and $(3x + 30)^{\circ}$. The value of $x$ is :

Question 18 :
Two adjacent angles of a parallelogram are $\left(2x+25\right)^{o}$ and $\left(3x-5\right)^{o}.$ The value of $x$ is

Question 19 :
Find the angles of a parallelogram if one angle is three times another.

Question 20 :
Given two parallelogram $ABCD$ and $CDEF$ on the same base $CD. $The height of parallelogram $ABCD$ is same as the height of parallelogram $CDEF.$ Area of  $ABCD$ is $50 m^{2}$. Find the area of parallelogram $CDEF.$

Question 21 :
If lines $x-2y+3=0$, $3x+ky+7=0$ cut the coordinate axes in concyclic points, then $k=?$

Question 22 :
The angle between tangents drawn from the point $\left(-1,3\right)$ to the circle $x^2+y^2=5$ is

Question 23 :
The angles is to be bisected to obtain an angle of $90^0$ is _____ .

Question 24 :
For constructing a triangle when the base, one base angle and the difference between lengths of other two sides are given, the base length is equals to:

Question 25 :
ABCD is a parallelogram with AB $=$ 8.3 cm and its perimeter is 25 cm. Then BC equals

Question 26 :
In parallelogram ABCD, AB $=$ (x+8) cm and CD $=$ (3x-2) Then AB equals

Question 27 :
If the volume and the surface area of a solid sphere are numerically equal, then its radius is ____

Question 28 :
What is the total number of candidates at an examination, if 31 % fail and the number of failing students is 248.

Question 29 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b1d103f59b460d7261f3ac.jpg' /> In the above figure, PSDA is a parellelogram. Points Q and R are taken on PS such that PQ = QR = RS and $PA\ \parallel\ QB\ \parallel\ RC$. Is ar (PQE) = ar (CFD)?

Question 30 :
The mid-point of the sides of a triangle along with any of the vertices as the fourth point make a parallelogram of area equal to

More from Mayur Sir

Recommended Content

Learn from Anywhere on Any Device