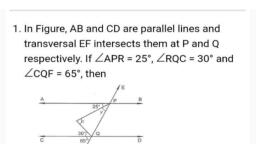
Question 1 :
'Two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal.' Which congruence rule is this?

Question 2 :
It is given that $∆ ABC ≅ ∆ RPQ$. Is it true to say that BC = QR?

Question 3 :
Which of the following is not a criterion for congruence of triangles?

Question 4 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b1d24af59b460d7261f584.PNG' /> In the above fig, can we say that if two angles of any triangle are equal, then the sides opposite to them are also equal?

Question 5 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b1d244f59b460d7261f57c.png' /> In the above fig, OA = OB and OD = OC. Is AD || BC?

Question 6 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b1d242f59b460d7261f579.PNG' /> Are the triangles shown in the above figure congruent?

Question 7 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b1d246f59b460d7261f57e.PNG' /> In the above fig, AB is a line segment and line $l$ is its perpendicular bisector. If a point P lies on $l$, is the point P equidistant from A and B?

Question 8 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b1d25df59b460d7261f59b.png' /> In the above fig, AC = AE, AB = AD and ∠BAD = ∠EAC. Is BC = DE?

Question 9 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b1d268f59b460d7261f5aa.PNG' /> In the above fig, ∆ ABC and ∆ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, is ∆ ABD ≅ ∆ ACD?

Question 10 :
<img style='object-fit:contain' src='https://teachmint.storage.googleapis.com/question_assets/cbse_ncert/61b1d26af59b460d7261f5ac.PNG' /> In the above fig, ∆ ABC and ∆ DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, is AP an angular bisector of ∠A as well as ∠D?