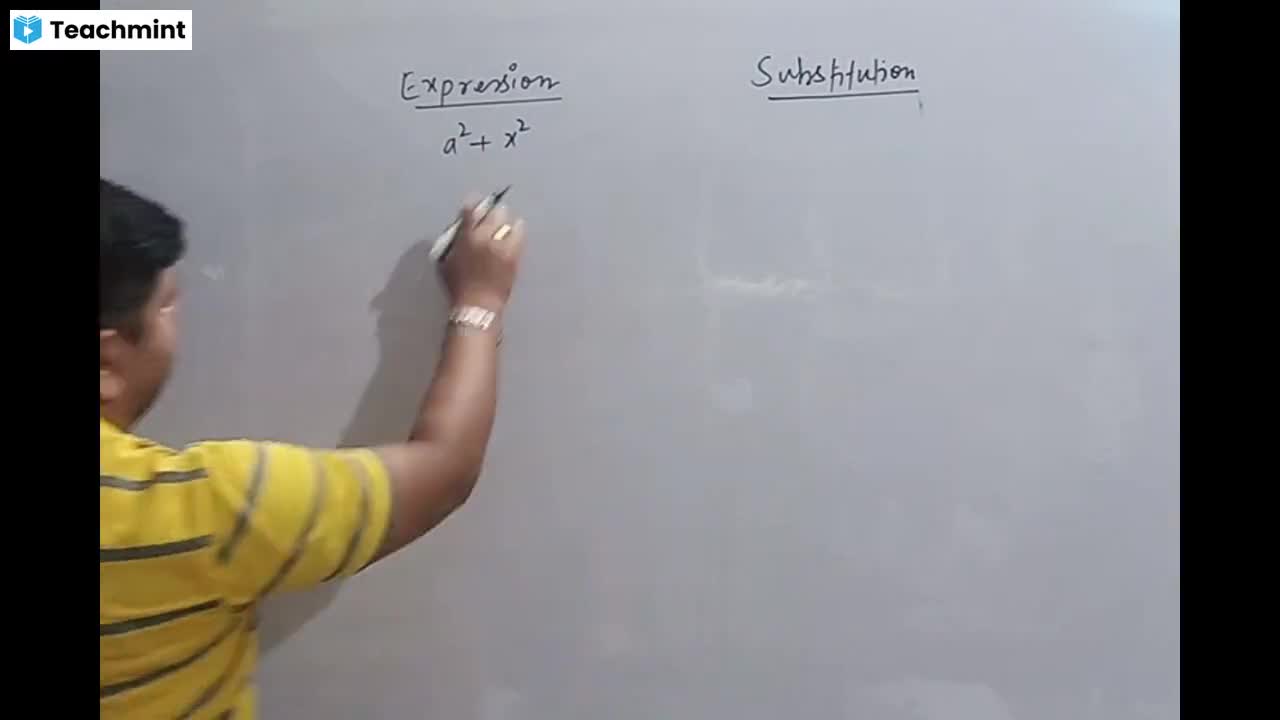Question 2 :
If $\alpha , \beta $ are the roots of the equation $ax^{2}+bx+c=0$, find the value of $\alpha ^{2}+\beta ^{2}$.
Question 3 :
State whether the following statement is true or false.After dividing $ (9x^{4}+3x^{3}y + 16x^{2}y^{2}) + 24xy^{3} + 32y^{4}$ by $ (3x^{2}+5xy + 4y^{2})$ we get<br/>$3x^{2}-4xy + 8y^{2}$
Question 4 :
Simplify:Find$\ x(x + 1) (x + 2) (x + 3) \div  x(x + 1)$<br/>
Question 6 :
Simplify:$20(y + 4) (y^2 + 5y + 3) \div 5(y + 4)$<br/>
Question 7 :
What is the remainder, when<br>$(4{x^3} - 3{x^2} + 2x - 1)$ is divided by (x+2)?<br>
Question 9 :
Divide:$\left ( 15y^{4}- 16y^{3} + 9y^{2} - \cfrac{1}{3}y - \cfrac{50}{9} \right )$ by $(3y-2)$Answer: $5y^{3} + 2y^{2} - \cfrac{13}{3}y + \cfrac{25}{9}$
Question 11 :
Find the zeros of the following quadratic polynomials and verify the relationship between the zeros and their coefficients.$49x^2-81$<br/>
Question 12 :
What must be subtracted from $4x^4 - 2x^3 - 6x^2 + x - 5$, so that the result is exactly divisible by $2x^2 + x - 1$?
Question 13 :
If the roots of ${ x }^{ 2 }-2mx+{ m }^{ 2 }-1=0$ lie between $-2$ and $4$, then
Question 14 :
Find the Quotient and the Remainder when the first polynomial is divided by the second.$-6x^4 + 5x^2 + 111$ by $2x^2+1$
Question 15 :
Factorise the expressions and divide them as directed.$12xy(9x^2-  16y^2)\div  4xy(3x + 4y)$
Question 16 :
If $\alpha$ and $\beta$ are the zeros of the polynomial $f(x)=6x^2-3-7x$, then $(\alpha+1)(\beta+1)$ is equal to<br/>
Question 17 :
The roots of the equation $\displaystyle x^{2}+Ax+B=0$ are 5 and 4. The roots of $\displaystyle x^{2}+Cx+D=0$ are 2 and 9. Which of the following is a root of $\displaystyle x^{2}+Ax+D=0$?
Question 18 :
If $\alpha, \beta$ are the roots of the quadratic equation $ax^2+bx+c=0$ and $3b^2=16ac$ then
Question 19 :
If $\alpha$ and $\beta$ are the roots of $x^2 - ax + b^2 = 0$, then $\alpha^2 + \beta^2$ is equal to
Question 20 :
(64x$^3$ + y$^3$) $\div$ (16x$^2$ - 4xy + y$^2$) is equal to
Question 21 :
Let $\alpha , \beta \in \mathrm { R }$. If $\alpha , \beta ^ { 2 }$ are the roots of quadratic equation $x ^ { 2 } - p x + 1 = 0$ and $\alpha ^ { 2 } , \beta$ equation $x ^ { 2 } - q x + 8 = 0$, then the value r if $\frac { r } { 8 }$ is the arithmetic means of p and q, is
Question 22 :
Divide :$\displaystyle \left[ { x }^{ 4 }-{ \left( y+z \right)  }^{ 4 }\right] \ by \left[{ x }^{ 2 }+{ \left( y+z \right)  }^{ 2 }\right]$
Question 23 :
On dividing $x^3-3x^2+x+2$ by polynomial $g(x)$, the quotient and remainder were $x -2$ and $4 - 2x$ respectively, then $g(x)$ is<br/>
Question 24 :
Find all values of a for which the equation $x^4+(a−1)x^3+x^2+(a−1)x+1=0$ possesses at least two distinct negative roots.
Question 25 :
If the ratio of the roots of ${x}^{2}+bx+c=0$ is equal to the ratio of the roots of ${x}^{2}+px+q=0$ then ${p}^{2}c-{b}^{2}q=$
Question 26 :
If the polynomial $3x^2-x^3-3x+5$ is divided by another polynomial $x-1-x^2$, the remainder comes out to be $3$, then quotient polynomial is<br/>
Question 27 :
Let $ p $and $q $be roots of the equation $x^{2}-2 x+A=0 $and let $r $and $s $be the roots of the equation $x^{2}-18 x+B=0 . $If $p<q< $ <br> $r<s $are in arithmetic progression, then the values of $A $and $B $are
Question 28 :
Find the product of roots if the quadratic equation $ax^2+bx+c=0$ has exactly one non-zero root.
Question 29 :
For the equation $3x^{2}+px+3=0,p < 0$ if one of the roots is square of the other, then $p$ is eqal to:
Question 30 :
If the equation$\displaystyle{ px }^{ 2 }+2x+p=0$ hastwo distinct roots if.
Question 31 :
Let $f(x)=2{ x }^{ 2 }+5x+1$. If we write $f(x)$ as<br>$f(x)=a(x+1)(x-2)+b(x-2)(x-1)+c(x-1)(x+1)$ for real numbers $a,b,c$ then
Question 32 :
$\displaystyle \frac{x^{-1}}{x^{-1} + y^{-1}} + \frac{x^{-1}}{x^{-1} - y^{-1}}$ is equal to
Question 34 :
If $\alpha, \beta$ be the roots $x^2+px-q=0$ and $\gamma, \delta$ be the roots of $x^2+px+r=0$, then $\dfrac{(\alpha -\gamma)(\alpha -\delta)}{(\beta -\gamma )(\beta -\delta)}=$
Question 35 :
$x_1$ and $x_2$ are the real roots of $ax^2+bx+c=0$ and $x_1x_2 < 0$. The roots of $x_1(x-x_2)^2+x_2(x-x_1)^2=0$ are<br/>
Question 36 :
If $\alpha$ and $\beta$ are the roots of the equation $ \displaystyle 5x^{2}-x-2=0, $  then the equation for which roots are $ \displaystyle \dfrac{2}{\alpha }$ and $\dfrac{2}{\beta } $ is
Question 37 :
State the following statement is True or False<br/>The zeros of the polynomial $(x - 2) (x^{2} + 4x + 3)$ are $2,-1 and -3$
Question 38 :
Total number of polynomials of the form ${ x }^{ 3 }+a{ x }^{ 2 }+bx+c$ that are divisible by ${ x }^{ 2 }+1$, where $a,b,c\in \left\{ 1,2,3,......10 \right\} $ is equal to
Question 39 :
Simplify: $\displaystyle \frac { 45\left( { a }^{ 4 }-3{ a }^{ 3 }-28{ a }^{ 2 } \right)  }{ 9a\left( a+4 \right)  } $
Question 40 :
Suppose $\alpha ,\beta .\gamma $ are roots of ${ x }^{ 3 }+{ x }^{ 2 }+2x+3=0$. If $f(x)=0$ is a cubic polynomial equation whose roots are $\alpha +\beta ,\beta +\gamma ,\gamma +\alpha $ then $f(x)=$