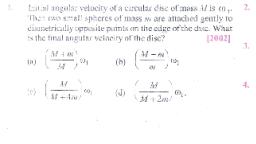Question 1 :
The set {tex} S = \{ 1,2,3 , \ldots \ldots , 12 \} {/tex} is to be partitioned into three sets {tex} A , B , C {/tex} of equal size. Thus {tex} A \cup B \cup C = S , A \cap B = B \cap C = A \cap C = \phi . {/tex} The number of ways to partition {tex} S {/tex} is

Question 2 :
Given two finite sets A and B such that n (a) = 2, n (b) = 3. Then total number of relations from A to B is

Question 3 :
If A = {0, 1), and B = {1, 0}, then A × B is equal to

Question 4 :
The range of the function {tex} f ( x ) = ^{7 - x} P _ { x - 3 } {/tex} is

Question 5 :
If A, B and C are any three sets, then A × (B∩C) is equal to

Question 6 :
The number of non-empty subsets of the set {1, 2, 3, 4} is

Question 8 :
Let {tex} y = f ( x ) {/tex} be a real-valued function with domain as all real numbers. If the graph of the function is symmetrical about the line {tex} x = 1 , {/tex} then {tex} \forall \alpha \in R , {/tex} which one is correct?

Question 9 :
Let A = {a, b, c} and B = {1, 2}. Consider a relation R defined from set A to set B. Then R is equal to set

Question 10 :
The domain of {tex} \sin ^ { - 1 } \left[ \log _ { 3 } \left( \frac { x } { 3 } \right) \right] {/tex} is

Question 11 :
Let $n$ be a fixed positive integer. Define a relation $R$ in the set $Z$ of integers by $aRb$ if and only if $\dfrac {n}{a - b}$. The relation $R$ is

Question 12 :
A survey on a sample of $25$ new cars being sold at a local auto dealer was conducted to see which of the three popular options - air-conditioning, radio and power windows - were already installed.<br/>The survey found:<br/>$15$ had air-conditioning<br/>$2$ had air-conditioning and power windows but no radios.<br/>$12$ had power windows<br/>$6$ had air-conditioning and radio but no power windows.<br/>$11$ had radio.<br/>$4$ had radio and power windows.<br/>$3$ had all three options.<br/>What is the number of cars that had none of the options?<br/>

Question 13 :
The set $\left( A\cap { B }^{ C } \right) ^{ C }\cup \left( B\cap C \right) $ is equal to

Question 14 :
Write $A = \{x | x$ is a month of the Gregorian year having more than $30$ days$\}$ in the roster form:

Question 15 :
A small town has a population 8000 out of which 3500 people read 'Times of India' and 3000 people read 'Indian Express' and 800 people read both. How many neither read both newspapers

Question 16 :
A relation R is defined from {2, 3, 4, 5} to {3, 6, 7, 10} by :$(x,y)\in\;R\; \rightarrow x$ is relatively prime to y. Then, domain of R is

Question 17 :
If $\displaystyle A=\left \{ 0,1,2,3,4,5 \right \}$ and relation $R$ defined by $a R b$ such that $2a+b=10$ then $ R^{-1}$ equals<br>

Question 18 :
In a town of 10,000 families it was found that 40% family buy newspaper A, 20% buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers, then number of families which buy A only is

Question 19 :
If $R$ is a relation from a set $A$ to a set $B$ and $S$ is a relation from $B$ to a set $C$, then the relation $SOR$

Question 20 :
Let $A$ and $B$ be two finite sets having $m$ and $n$ elements respectively. Then the total number of mapping from $A$ to $B$ is

Question 21 :
If A = {1, 2, 3, 4}, then the number of subsets of A that contain the element 2 but not 3, is

Question 22 :
If X and Y are two sets, then X ∩ (Y ∪ X)′ equals

Question 24 :
Let X be the set of all engineering colleges in a state of Indian Republic and R be a relation on X defined as two colleges are related iff they are affiliated to the same university, then R is

Question 25 :
Out of 800 boys in a school 224 played cricket, 240 played hockey and 336 played basketball. Of the total, 64 played both basketball and hockey; 80 played cricket and basketball and 40 played cricket and hockey; 24 played all the three games. The number of boys who did not play any game is