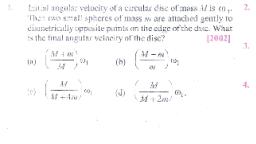Question 1 :
How many of the following statements are correct<br>A. Yellow mosaic resistance mung bean was developed by hybridisation<br>B. Yellow mosaic resistant bhindi was produced by mutation breeding<br>C. White rust resistant mustard was developed by hybridisation<br>D. Pomato was developed by somatic hybridisation<br>E. Golden rice variety was produced by transgenics
Question 4 :
Which of the following in sewage treatment removes suspended solids ?
Question 5 :
Ornamental plant with maximum number of floral leaves in its reproductive shoot is
Question 6 :
Abdominal spasm, vomiting, Internal bleeding and intestinal blockage are caused by which of the following :-
Question 7 :
Read the following statements regarding Euglenoids and select the incorrect ones :-<br>(i) These are mostly fresh water organisms found in stagnant water.<br>(ii) Their body is covered by a protein rich layer called pellicle which makes their body flexible.<br>(iii) They are photosynthetic in presence of sunlight but become heterotrophs in the absence of sunlight.<br>(iv) They usually possess two flagella, one long and one short.<br>(v) Euglenoids are multicellular ciliate protists.
Question 8 :
When the largest posterior petal overlaps the two lateral petals which in turn overlap the two smallest anterior petals, this type of aestivation is known as :-
Question 9 :
Match the column I and II and choose correct answer :- <img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/NEET/5b02ced57f6cca08b9fd9b89">
Question 11 :
Inner most layer of the extrastelar ground tissue system of roots, is characterised by
Question 14 :
Choose any one of the following four responses.
A. If Assertion is True but the Reason is False.
B. If both Assertion & Reason are False.
C. If both Assertion & Reason are True & the
Reason is a correct explanation of the Assertion.
D. If both Assertion & Reason are True but Reason
is not a correct explanation of the Assertion.
<br>Assertion :-Multiple alleles can be observed or studies in an organism.
Reason :- Multiple alleles is a rare phenomenon.
Question 15 :
Pickup incorrect statement(s) about enzymes :<br>I. All enzymes are made up of proteins except lysozyme<br>II. H<sub>2</sub>CO3 molecules are formed from CO<sub>2</sub> and H<sub>2</sub>O in the absence of enzyme carbonic anhydrase dramatically raises to 10 million times<br>III. Formation of Enzyme substrate complex is transient phenomenon<br>IV. The energy difference between average energy content of 'S' and transition state of reaction is called activation energy
Question 22 :
Choose any one of the following four responses.
A. If both Assertion & Reason are False.
B. If both Assertion & Reason are True & the
Reason is a correct explanation of the Assertion.
C. If both Assertion & Reason are True but Reason is
not a correct explanation of the Assertion.
D. If Assertion is True but the Reason is False.
<br>Assertion :-Atlas-66 variety of wheat is used as a donor for improving cultivated plants.
Reason :- Atlas-66 have high lipid content.
Question 23 :
Ringworm is caused by fungus <br>A. Microsporum <br>B. Trichophyton <br>C. Rhizopus <br>D. Oscillatoria
Question 24 :
Triose phosphates produced in the following diagram are :-<br><img style='object-fit:contain' src="https://storage.googleapis.com/teachmint/question_assets/NEET/5b29766935e93a2c2bb471ed">
Question 29 :
Which of the following muscle help in changing the position of testis to keep them at proper temperature?
Question 30 :
Sphincter of Oddi controls the flow of digestive juice by guarding which duct?<br /><img style='object-fit:contain' src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAOcAAADgCAYAAAD48XGYAAAgAElEQVR4Aezdd5CtS1X3cXPOEYQSU6ECKmIC0zGioiKKYKiitFAUUYI5e8w5gCIYQf3DQhAMgBjAizmBiBSoRAnmnLPz7s9z73dc93HPnjmz95x765Wu2tP9dFi9evX69VrdT5iXOXppeKkEXiqBG6UEXuZGydVLmXqpBF4qgaMzgfNf//VfF1H9y7/8yxL/93//9/VE91//9V9H//mf/3m9PNfq/dM//dNxvjx1hWjI+/d///fjOn/913+9pP/5n/95if/2b//2uO6sN9v/27/921L3P/7jP67Xn76Uafd3f/d3S53Gou7/9dDc/PEf//GxKJqf4uOCHQl1yXjb/Oxodlz0D//wD4te1H723XypPPNdb9O5dZ1oqp/+6u+soTbpY/xcDf3ZCU4MzMHNQUkDiB+B+AUYAy9dHTFlSKAGLV09bVIS9YAJza/92q9VdPQFX/AFR9/4jd949HVf93VH97///Zf0u7/7ux/nP+lJTzq65pprlrporoG6FGz+pJDxUf7/9diiaCEU1gp+kmzIOWU9a5tJK4Vf55mjtfIHkqlnU3eklVXu+vnPf/5C2ti29TX7PSk99X/WOSl/1tk3vROcEX/qU5+6JL/iK75iGXwKPoVT3RkTlMkTrwOBNbFZPgOOtvom5JVe6ZWOXuZlXubo1V/91ZdYurwv/uIvPnqt13qtJf8BD3jAkq/dS17yEtESXvCCFyx09PGXf/mXS95pfF/X9P/7yAJF3mt5/NVf/dWZxp6CPvOZz1zqt+C6OCsY6MY//uM/Lh5OnU59+fM///Oyjy3fccaOxHpMqgb49G5H86WoMdCdF73oRcfV8Xs1wk5wmrwYjJnAM61oZWJC0Y6ATV6CFivzA0wTmrBcz4A2gQDhl37ply7gu/3tb3/0+q//+kcv//Ivv/yAtN+rvdqrHb3qq77q8fVv//ZvH/c76ZamfPFV3v/l2Jw0r+TASzmrAms7w1nb1cY8P+MZz1j07G/+5m+W7LYgLrLm0TVvP/uzP7vohzRdW/MQbfGzn/3s48vozrEeF25JZK0rmv2sy6pzyHgnOFNgICIcYMNUgsKIPAKOcW3kBbyY1U6+oK509KvzxCc+8ehXfuVXFpC99mu/9jHYXud1Xuc4DZCf+7mfu4Dxjne845IPmJ/zOZ+zuLrK5X/VV33VUvbrv/7rR3//93+/LAj6wfu63/r/vxhbfMlHCAhnlYN5J8sHPvCBi15Mi/KCjcdyWkhHWujTj0Aqnz4EhAxF7cRTj+gVnqIz9VT+DEB9lqBPY2x7lRd5lrb71tkJzoQwB6nDOYkEkTCUBVLpKZCZr6yAdgJmJb/kS75kcVU//dM//YhFBDYr3ld/9VcfvcZrvMYCTHkA+fmf//lL+Su/8isvsfyXe7mXO3aBpdURpuKcdWLi8f/nuIXqz/7sz5ZhmvPpSp42dsBpsRWfV7YBdOpJ+odmOihdfrzNNmt9/Iu/+IulWuPc1qa8bTF6+ly3j99tbQ6VtxOcDZowptAT1JoJdYAg4QXa6KhPWM95znOO/uRP/uR64FXGdeW2Ahlg3upWt1qA2r4ScAEOSNX5sA/7sKNXeIVXOLrf/e539Lqv+7pLe2lW94M+6IOOvvzLv/zoHd/xHY9+5md+5ug7vuM7jk9s8bMWtv7/r4XmZy6iZ3X5pqxSVEA19+Q79WXWXadZbe1tRbSLVjzN/e+2OdMfndvWH6v3sIc9bHGZ1YtW417zsr6OZha78vPIqLZXEu8E55oQwQU0AySsrtXljtg4d/BS+wTtOmFK11YewAMm6/llX/ZlR+/93u99dOc733k5mQVAoPy8z/u8xWK+y7u8yxFr+V7v9V4LSAN0IL506dKSD5zqZFnxGy9rgePn/3qwiAnm5azySVFnfe2T8y6ZmvdCrnXASTecwguz7uMf//iaLbpG53KFFWgbkAN79GqYq9z1SfGsN3X3pPqHzN8JzimoBnnIztEyiV/5lV95bC2dwL7ma77mohysI2D6Sfu93uu93nHadae480DoFV/xFY/8srD2ny/7si+7AF2frfDSJtGvVdIkzglR5yLDVJoUSn9TGfftH93Zz770ztp+W58t6pNGnlhy39Zu1j9retJpfrWd+WeldUPU2wlODCU4aQNMaQ41wGs29yY7/OGCBjKgYxHdvgFCFlBZVhKA25MqB+r3e7/3W+p+9md/9tHly5eP7Fvlve/7vu+Sf/e73/3oJ37iJ44nx1gmIIzxagZ94yFZHlqBoqufxmkxtNC28F7keOsT6PSbNXV+YNx+k49pAGb6vDz+/M///LEXpy+6nCymrM9L/6LbnQrOefiDmcBqsPsGgnKaClyAl1UENJbu0nXuadbxVV7lVZa6HQTd7na3W05mJ0i/53u+Z9lvovkGb/AGS33tnSje8pa3XPrg7jaOOQZKlELlZs3yi0gHoIugnQKKGxf3097rEMp/Gs+NTZ+BQpsv+qIvul7TTkDX99GvV+mcF8lAc2n69qu/+qvXu3V0TtIX3uxUcFJiSmuFkw6UTfY+HJo8Lm3W0KQB1Ru/8RsvsfwA+03f9E1LXkAWZ3Glc2GltcsCOwJ3306+AyWxPai+TVart/G0shvTnNR9xniWtnhJkePrLO1Oq9MYxNE3XvvE5vE0GhdR3mkwvuZeVV/tYQ+1eJhXNOmwMYuTy0WM7ZA0d4IzASWwOibQQwwQGH75l395AczXfM3XLHvLDm8cAHk8D5g+8AM/cNlDfuu3fusCOm4qAHJ124/e9ra3XU52WVeWUbt+gOuxPye6aMm3Dy3MseRmHWLxif5JcQAhh/rFCwU6ZDCWOZ453kP2s41W41ImnU4ZYzyRg4VfufxtXs022leSN8eM/lqnr4TW1aq7E5yYMAhC5HIIuSDLxQH+2GcCT5bv3d7t3RbA6e9Od7rTAqRumQQ2hz2lub+sq9jDCm6l5OYCai6xfag2lzd7UQ8xsMSt4HMYPdN7aIDMPkqnuOKpPIfu2/xFnwVtUYiPi4znWOJBHp7iYw3G9VbqvPwFwknfQri21uelf9HtdoKzVQ4TM02ZEuy+DLKUAAM4QMcSsnCBL9c119RBkLJc4Q6M5KkDkG7HeEheXrdX8NmeVT5L/ZCHPGR5OsaE+Qkp0HJxwX+yHOLcTul5W+AQLEz6+mmsh6B9Go1tQOh+Y2OmS1PuE0yn0d9VPvvufmr1k33XN8Z4JzgxnABbAQ8luIQBKH5A+CEf8iFH7/zO77yAVB5rKG7/CMjucQIzcFbOOgLeHe5wh6X+B3zABxy967u+6/Jsbie4ucus8Bd+4RcubYG58RU3vsYbnxcRp5BzcWC5n795m+IQB1IWUeNaK+KhFtazyGQChGzjZRsPDEDzkFdxlj521dFfc6oe+vN6V9sbuuxUcJ7GYErcJDTwhJ+SrYXdJL3P+7zPAihAYc2A0X7zPd/zPRcAOXaX148ldJrr2v6RG5yVrM77v//7L+XAi5Z8aXvUz/zMzzy2ph/8wR+8TBbe4j++G8dp4z9LOZrRrX5K2PW2ONkqC8ilJ714j0YPgWQhk3Xl4vImXTTX8zTbbEsbhzaNZ3pY6s8xoD8fo9xGb+apH3/xWz+zXjRnX7P8pDT5THrJ8cayH90bnCdNZvkJjBASMIGXDzgsXyDi1qoXUAk21/aN3uiNjoGWJdSeZZ3t5fXgu7g96jd/8zcf70ezuuuJM2G9vbAuu9LrJrt2rilvsil/V0xu2iQvdcmP4s4FBN/qJeMWxTXtytFI8Y03V1N9dSbtNY2u55xK40kQoxH9tRyuVPkDn7OC5NAcGfeDHvSgWDqOPR56WsBffEd3vbicRuMiy/cCZ0InoJPed2uCCGGbwnTa6jaHtGdigWveDsmtld8hETByXe95z3su9e0zgTBQqsvVzYqq75FA+X5OdLnRDh/wPw8hUuBDCB4tYFzTXF+ftS8yTJG0SUlrT87NC5DoW5wiVq9Y/QKeAlh5u+I1zUBEngX9q7ce71lAgDevE9a2OXL9hCc84Xjv3MKi3zmeeDgtbhx41X7K97S2F1m+FzjXg5iCUWaiCcwqTKme97znLYJu8rin3FqveAFgLi6QOcUF0E5eHRL5AgJgqev0dVpPljALKQZGK60TXM/oaoeesvvc5z5HXFp5ACw0FvG2ReS8k0AG0woB00/91E8t93dPo4kXVsYBUTLTJhBNZaS4gfIkq2F+/NSjkNHKDXb98Ic/fNkmBIil0gl/jCs6xolXcXma6QutfV65mosb+oFxsiVfPUF/UxdnvZl+wXitzcJC3h5W0X7Ke7a5mum9wInRKxH+n/7pny5jS4guAAhIemfTLRWAYUVzPZXba97sZjdb6rr2InbgdIJbGvjmfc7Ajb53PrXtwYbA3Oko4HCnhfKWiz3/mGiTP0F6FuWf3VKc2V5ZCrhNkeTpY5uFqj6rFJDQmvSjPXk4KQ2UtU1u5hjPM0ya67JZrzT+W3DEAFiwGEXvWc96VtkLQOVfiXzjPSLR7fqGivcGp0kwwWthtP9ZD3w90HngwyK+3du93QIg+1CHRDe96U2X52NZwnvc4x7LIVAPJ1zenNoGPqDjwgKtX8CTD+x+3UuVniCdPOU6zbzzpoF9n4lmbZ7+9Kdfr3vAmovbN3zDNyzlQJEi924m8L3whS9crEBgVXkNWPTmPrD21+t4y4VT5YL5Z9G+8zu/89jVjh99n7Ttqf22OJ6SobdmJkBLp3tXCsr4o78tFn1yZcp4G29XI28vcLbqNsgYTqgmiyvLapggwtNGmmAB9+u//usXoHQA5FMkWcHiCaruW3riB8BYV+9qSvu5TdKDB1xh7rFbLF43U/7hH/7hS/yhH/qhx23wjR8/E91ENZ5DxMacDNBL4c5Km4y1nwGfXNLmQVlzUd1cdGNT5vfc5z53ARL5z7YTtOqfNVDklLnvNyXD8te0TsrfVg+PLRjxG6/tuf/wD//w2ECYw8rX9HZdB3JyudL52UX3vGV7gVOnTYK0Ce1QwLXQ94EabMK9tvTo+GsG0wJyaR3wABOLKT3LAZBl7IGEDpXU7WQ3y+khBel5qMSyoi0f3RQZTylNSh6f54nXCp4M0Jrpk2gnK3QmrfJrl3eCd2kWN0Xb5gmk0Gs+tDkLX/Wrv/qJv7Xc0o/y47X60doWt7BUZtx+8Zgc6sN16drsiqOjjrHM8exqd7XK9gbnWRkliCnYBOPF6oDkpLbXu4Am0LF8wOVEN2sKXO6F9uZJgJPPbXUyK89DCO1dXb/He7zHAkwPKlT3yU9+8vGikjKbqCa/Mcaz69Ip5wR4C5J68lPI2U5aSAF/4Rd+Ybl/y80X9C/gYdKWlyylBTzEh7LaSus7Xtftrm19/r+7AIZnPAFlctR/fJ6/1/O3jN9k7nobP/Lxndz0ONOuG5P0RYULBecc0DYhNChPBeWKAlIuLvDkxhZ7QkjaflS5H4Dab7q1AsT2pN02aX8pv6eKLAjV1X79jG2TN/mP12Jlay/BhAUME7wGlbbK/ZpcH7BCi/ttXA6z6r++TopTtmidVG8te9dr3k9quys/umJjbezrNsrjVZnxnlR33Xafa1ZUX3jTf1Z1Pfb4b0GpT21PCrvKTmpzpfkXCs7JDAE0IBOTAtqfThACUNZRmqsaCMWd2LK2b/iGb3i9sqwngPtpn/WdNDoZLg+f9ihzn5IbpqyJnQqVsplQk+7a+DqtdK2sAEB+5FDIoorxgl+xQC5r0KGHx+gmTzSji0fKp/85Hmll1YuHQ8V4WdP3kfB4nGNJdofq+zQ6J/WXHGd7/KrfrzJja57Lu+j4QsG5TREM2iHG8zcnfZSySaOUXM3AKM4dLZbX87MBq3uYAA10AOrEN4upHhe5hxOc/srrlJi1ct/RS7gOmVLo+DIGC4kPkwGeSTKBjS3la6KUC63S0k2stBBtb+r74Qe/eQ/zi3HR1wYfZCeOBnp4Idd4dXjCtTamFpnoqB9QpfcJ5KHfGZLNzMdXY5p1Lzrd4sczwheZNX+uff/2KU95ytEf/dEfXW/rga/GIdbGWI2B7Jv7i+b/QsGZwhjgDPKzMPIf97jHLQpKObMent5xuNNXD+xHK7t06dJyWwRYpQNqcRYVUD1RVLssMiBIB3qT2CSkzE0s/qRNygSc/E6lpSmAcTVmeQKFWAOJZbNq/9Zv/dbSLv4sKg6/BP0V8BZ/eGjF15dAWZKxtDFMBQJWH25uLzzL6uM8sQXWYhEfk4Y+nMTPjzorN+9z7mebQ6ctQvh4weZhgxbN0/pQf5t8yN2cTL04jda+5RcKzpgz2Fas8sQdvpQXuAKNa4rLhU2BWcGZtj8FQrdbfElBeXTEgGh/Ko4uYDpc6iCq/tuLNJEpfOUznnWmVTDWAK5+QJJeA1We90qNJ+ueYqTwrkurP0P5tamsxaC+lU+lkm6stTlPTFmnHNZ8JD/5eST6Wdc7T99X0mb9RBG54EGMfz9pckmm6De2bX01tm1lh8q7KuDEbAJoYoqVBdIJKgc83NS5ZwQmh0fqBTTpwAuArrmq3kCRvtvd7nY9sL7pm77pcj1vrRD0VF48UV48b5sEeSk+IDppFVgorqQJrnzSbZzqelpKPTz25NK3fdu3KTq2mvpRZyrMNn7IMnkCZn3Gw0J080fZpFX+oeJ4QG/yqd9Zdqj+zkIHH3k85EImHoiYi8Wko755r+4cR/Wq0/VFxRcKzrVyzEFQEgBolVf2qEc96ugud7nL9cAEaBQYGCegAJLFzPqpwwK1b+tzJPLlTTBzHT3HW9tv+ZZvWZSJ0PG8TYHlrcEaCNxLZbUtDk6KZ5iub9aKe6lPAX/ccLd40NglM/W38bFW/sn/HM8E8TalQ/9KQjTEeOg6Gvqb4+l6Xa/6h47xZM4K9ZunE9/kNfWw+sXqoTPlWtlFxjvB2YqTm0bQBrFrIFfCbBNnFYsmZeV2UvS5R5Qf0MRZ1A56PAGUS2svWjkAqy8vGtLle4rIgUDhSiaAss3Jt5fSr1D+3DuiXT5ejJ+1jC97NKFVfYIpWQV2c6NcaH7E8U+hKs9io1Gedi0W2qmvrXKLjuv6FLtOH7QV8CK/YA7RiB/5tSmvBS0+G4+6ZJO8Kpe/bzCmyeekF3/y9JlMZp0bKr0TnJiaT5MkyJMGep5BzHuMlNtDzCmr01sAtZ/svqWyrGn1PDHUIZC8gCkNvFnUS+PwaFpS+75AY3KuZHzq29OSU18NnHJo0Zl5pZXhI36BE70Uk7wpdTIKLP0f06lYlF79xlFdfTWe6HYwFG/i2sWb+Jd+6ZeWy3mAox90aqtd6dk2EG6jq578gPiCzYGNYKHCa4vTkrnHn8YNnC1K5IL+5LuFo67S865vqHgnOBtQMSZNzBzYPoynFCkSITWZuZwB0HXKL89+NMB2QCTfGyf2q/LmwwzK+q9krLInh7jJn/VZn/W/PlrWpJ51bD/3cz93/FC9flIugE1x7UfnNdq/+7u/e7wQeea3f7qkLEBKF8gmQKb86E+51Z+68dGcRSd5u65+dOWlzG4xJQv19BnNqROUOYuTF6JeSq+/kx58b8HQr0Wg+Z/5ys4TGps4fvHkgKhx6G+W10/lXd8Q8U5wei/QR5oNiGt00nuCh2B8faLmNBWIuJ9A5Kkeis8lzd3tWv/qqC+vfHEPzatTOjCjBfT6MknGmdKnbNqdFCiTSffJTn1xq/GRQmtHyQJD+dpRCLchJo8+oTIDwOCrh8lnmX7nfOgHzaxRfWnTmGa5euhvU8Lqa6teliSZKG9MvQboHrG9vfzqT8CjNXmqTN2Ao07pQ4OzvtHVZ/TNuT73ed8U3xcRdoJzW4etNNvKzpNnwpso7Sku4f3Gb/zG0eXNK2EByIGJNGX2kS5xhz/zC3zANkGqnl9vv9Sml62VUaz14nAlY+k+rZNkp8Qm2wkui+ql8F/8xV9crKZ3V/u0qLEJwGxcfiy9AHS/9mu/tijz0572tCUPf75UTskslG6eF+bWg9JRuEKAcm3uUtLKi5UV8I/OlMk2wAVQ7fJiolHZLuWPZjx5s+QigvH4FSxSwtQ71/GxrUze1Q6ngpPrVWiv0vW+8Vyh0U4Rm9iE6Kkge7Meu8s9BSzP2gJnoLN/y5198IMffLyn88zq3KsC8V3vetcFuF+8+SJDgTLr/yxjpcDqAb4HJigoqwxwHsr3EL/Pb/awfQtETzmVzyvo1o8xeZ2td1aN7dJmr2xc9tbqGcs111yzfE3hAQ94wPKOq0XAu50WGntg1lyefbtrB2b3ve99Fy+Bp3B5szjo6/u///uXNsavjmd99WNBedLmP3zZjwOpBybQBzbWNkXuo+DRY2nnvLaYT3DoC41ZT94M6cDMO29a3+kSvqfVRFNfJ7nd5+3zEO1OBadOmghpwjaYBitv39Ak2f81iRMcVjgKT5m4uSwjZQ2suakdCrkl0SFL7bTtp11fYLBHBQ4WOz6udDw9CogPILW/JB8/yuzWDdr4thDIx4OQN4BfP6GnovBrUaqOsfcVh/rsrRx1q9c4LUDRsDC9yZu8ybEMOhDzAkB1xOstQ7TEAoBOKyufOy9P2wIApCPTkivPYkqr0wGXayHX/Nqr/f/SqXRYPIE/xzJ7Oil/1rno9E5w5hIl5JQ3AO3LXPTRacIIpZUt+hTaJzBNPgWkUJSLFXEdOCnKBCVrqm6voSnvO7YprrYs3hybxeAsk1Mb45iu9EmTT27JjivK9U25xX7GXnt1/VPZ3Ev1LSKCBahvLhkDi6kdi+dHCQGY9WPVxPa4LCrr+NM//dNHvkb4/M0jeP5fDWusHkvt55rVtVDwMPRHJnMM9MLjkckK/+lKY5iuo7Ftm3PjSZbRkrdvQIscknn0pn7FXwtIfMw6tbva8U5wEnQrTowRehMgz4RQfqEVb1o9dZsodaQTiOvTQm0Jy68H3VkRAO2Fayu6a65ZAOXO9fV4ytb+Ds+ATvmk0aqf+JnXUwYmb5YBzhOf+MSFXtYIjWRkrCZ+Kkhl6nF/WyjwIsy63TDnEjs9xTe3/dLG1fXARjJfGm7+kNG2Q57KZzwVMWVsbGuQTBlIK89Nx3dj4BJHq77IqL6MfdKqzo019i8j12Etm3X5oa53gvO0TlICk5PCzcMJ7VuRotXErPMr3xanDGKTHyD168fVW7t0LEnl8zMm6OcOAzFAcWuFbnXYqwnGZCK2TQYlTpHVVUd/07Wb5cbrIGcCjxWxYOgH/9zOeTJLyX0wu8UGfePnOqPdbQvtk/955Nti2V6yhxaiZXzbQie1+HTrB1/rYFxC/FlMpgzW9W9M1y18ZP2c5zxnYU2al3eabA4xjlPBiRmTJp4hYXOdmgCTHDhZz1wYeROMKcOkty2dqzvLfvInf/Lo0nUPE/jeEIXl1r3TO73T0Ud+5Ecu11zM29/+9ku6x/j679msvPq5txNQJwmcMk0A4Ic8uJiNhdvXogHswJrMjH0CnHupL7/11+rRZokf+9jHLgc5rLuxcdH9u3W8rPlMtvKn14LWaaE5Um/K2+tUQGfc9ScuHV3tjdNi+BEf8RELDTLRXlsn1srV6+NZ2q7pRO/GFjeHN8SCshOchGv1oExi1wLBprAdUMhvINLbAhpNSkq9rd46TzuTO5VHHcDyY/06iaXErBEQOojhstqvque1KcCsnfjmN7/5cv+zm/7t6eKhMbvG8wRZdcTcNvR8ld5hUw/DT54dfERPfQrsgYn46fDKrSL7aW6jE921mzgPUPJe8IA/AMDjSXyqV2gOHv3oRy9Zzc1aBtVXjpepqHM8uYAtFrUrfvGLX7wktVmPqTo3tnibLOjj1eB/JzgJCuBSSpPTBCZEykfhZ/Dv3ikNBQmw7Z3mSj3bbEvXtj5TdIKR55g/xbZyT0sqv4cOpHMNZ9yzuMpZsILxUiD943etjCmkiYs3bePF/itXWf4cszGQS2OpzYyNq8lPBq4pfS5nezj0hYBmkanttSVn/6vdaaCe45Ve86E38qLAggOnGZRNGrPsxpZu3vIG8bdtvBfF96ngXHdsAlNWzHfgop5BUBKngQHD6t9ENfHadwK5pr/tOgWtfbEHFVLqvhDPvfQwQBZdObAAYocW8lisvkfEDbaXE3gJwlz9gTFAKosfacFCxL1n7fTDklPAJnXKLN618/ACnixu2lhc6l+9+gl4gS66k8fqoHvWoI1xTTqUz1hm3xaSxj/BFT/F2pbGQzS0T6nn+M/K5w1VLz2fssV/8r9ovs4EzrnSEb5fecCwtpwm22R4JAoQuJyO7ttrXemgCGf22QQTnn5yafXFNQQQe87u62Uhc2lzH4u5vk5NWcIWEjx24CGdxZJO0Zok/PAM+j8v+HD7QSCL+HX/U2DdWHBBXYdIgHnve997yetPSgEY6KfslU9QyWtO8lqqtyvOOngqKWVMBuhJW0j1pdw8GE99zbR+XKsbmDu0igf9aZsMy7+xx821sXlAv7m5SL53gpMQCduEbAsmy2GQ1R+z6s5gAtzC6OkdZWhNRZ/11+lcv9pVnmDiCw+U3Gmh+PLmfp3Yz+JB+QmVqwmo6rNU9qQBVl1pdd1XVcc7lx2wpMR4mHy5JidAd38QHZbY/UF9ClMuAQzv+tFfvKobANC0aGhbG+X13V5TeYp+VrmiI8Rfsbz6SrauAbRrdQAPf0JzgY/qlBfY1a9sabT5E3i7vrHGyQN/AXTO50XyvROcZ+mYNfTo09w4m7gmBg2Tbx/VkzKzLOU3WVMQU2FO48MD48BGyTuV7aEAt03crFc+gdjeEzgCSDQ8lACcDpJYwPm2CF4ChnTjxruT4ejqv3rGWz33YQX3YPGrH3zdYfOIokfhUvripfIef9agIG8PNjQHEySBHLicst7QAW/xGS/p1lnls0s/G3uLievS9XdDxnuD0+SzKg10DkZZSmmynTwCQMBbK462hP6C697vm7S2pVMmZawMJR9pGnsAACAASURBVGcZb3e72y2K3x7TflS/gOOXO1s5kAAooDgYUu750yya2N5ZMNYWkcbG7bu8sdaXNrd4uMfq23+mQK20xv2YxzxmoRM41cW3BSDFQH+bbJaGV/in/V4LhebxIz3nrXkBiPlMtXo3dCDLflfCyy79RCdreIh/53AlfJ2l7t7g1ElKKG3i5+TPcorgXqCb/CxcyqBOtzJSyvWKqc62wBJw5wKa2Mktl5HiA5zPYZoE1/2AtK8ocL1rrzxL2mmwMvxMficvKT4XuhPj7nV2wOO54YKH1fFlwdAXcAodSlXv0LGFpYO45Ju89WVxaC5beA7Nw3no4ZXu+MX3ldBpTNpM/Wzs0VSv9JXQv6i6e4HT4Ay2ARmcVX+Ck+KmvCZc3Y/5mI9ZQAIg3nYQCJ7ya+vgZAr0pMFPy+nks4MfVoviAxWX9ra3ve1iDfXXwwcsrZ96ABk4uabadx1NgMcbkHM/KXqrLv6iE/jRKLDCQIvfvlOb9WZttfHsqz2u21D6SXGicd4Yn9uA5oBOmHOlz+byvP0dsh1+TtKDvJdd/Z2mn9He918I7uJhn7K9wGkigapB7mIkIOW6+Ue4wOIf2W4LV6Kc3dvzkEHgABauo6dr5DmU0l/lYq9msVYdWMnrYfL2rN77ZNk8z9oi06THN0VhfXunEfBYzqwmlxdt/x7PLZwsc6+Fqa+Pt3/7t19uTXmX85DBHAn4LN08rBeCs8zlIXk7L63Gsav9lejnnFPtbgxy2AucuwRjcBSAEFOE6s/nR7sfqowlOsl1rO2MZ139sRICIHAbgcATO6772TvKZzWrJwZGeVlMeT2OJ53raSwtNPqK58BcDJACnvCCRj8LhwXB2PXnGvDrD4haCBYie/7BL4XzyztJ+czPtJ66klf5nl0fpDn+nBjP+TaWfYLxZX1z9V3fmMa9FzjnQKRTAOnKsoCUOmEQauX2nl7rEvvnqMI2QC8FW/5Ml80kAotH2HpkDyCAwKmtvV4AkO8RPw8rAJ6vrbN+7o+2b3S4w6q5j+owC/9++BOMrVsbLGUgFDuVVZerOq1lX3EIqL4dJDzhCU9YgHqlt0OWxif8mbIpTe7xXLPmzbXy5qzyGzrGr/u8xpDs1wvKNh7TMWXSjVO6MnP0oAc96H81n5+A+V+FVyljL3AmqHh1PVc0AsjKrN2G2qQ0Dme4lNpLX2mY1llfHh4XcjWBgVWz5+TuThdX3uTbHtVe89JmP5gl9dST0G0Vlq0J1jawBdC+S+uQyEej9ek+LMCzlFlPbrVDLU9azQOh5LJ0uscfcki2udnImas5fwHSWGb+Hl0frCl+eCDpEsJnAed6HK7nPMdgHtfUocpuyPgg4GxQBl/6rIPKUlBu90FT7tqjaXUrVH/mNVFzMag+wQdEMSsZkEqr68VjvLOAlfdQAcsbKKMrxps+8VIb7qwx8AQKxqUcADoImn2j4XS5bwhRoMYUjV2x+mgELGkhC4k/LuGU2aRXu5lnbBcd6kM8gVf+uv/GuM7f9xpd8m6Bip78ZBZPVzo30TpPvBc4ddiJ5XnuEzUhhJBgvDQNIKxoQCcQIFNPSOnksWBTkdHULmGqn9W7zW1us5zc+sQmi8aqto9BSxpIHBSxbMo7rfWWSXX1H+/xHTjtJVlbp64WkvnR6D4pkmudh8AF1j5r30sCeN8VyMVvBvwkp/KbI9dZTzJTzy86s91MR+ci4uYY7eYNP/rHo/kNIPGp7iH4Q3cbnfqeOtSh48zDx0WGvcCZYqYgBlX6LEwndHXnJAEIYHg/EyB61lM9bWY7eQKwAJgQD2IuY9dL4ebP8573vCU58xuLfeitb33r4wf3OzjyMLjbIIVOVPVJiYDLUz63vOUtl/S3f/u3X+9dTf81rQ+PeUfzgQ984PFjjJ5BNmb8TJ7q66RY3bVyUZ5ocI2Tndg1y16b4pPoX438eDB/5Ng86Bswe67XtXEFjmL55w36OyngKzmu6+g7ua7LDnm9FzgT7D73idDIEhpY6VxKSl8wUYQSkAOjcoJO2Fk4+Ql4vYdbC1c991ftC3ODHRDpn5sKnOizQtGKdnLgsjoJZhk/4zM+Y2mrfSe40jwDof6NV5/z42bKs8zSp4X6r94EqLwsp/yU+iTrjNa6fXQPHTdPZOD7yPpOLsoAVVmAjTd8NI5D8USn9L2Wuz7Nt4XiIvrdxf//aP6uWmcoI8DAQWkN6izhEY94xHG1KRhfPPAYnoMSp7nr0N5TfmCpToI0wfFUGUC3AFDaFLdyi4JXyQC0/aG3WxzWTIVoYYi+53uB0mESELK4/Ue09pdoAmf9UwhyA2h73qxHvJwl1r/xTtmRPbotHsqlueZzDOhrP9079eQFiLPwcN468ayvH/qhH1rIlFc8+cVbYzpvn7MdWmRlvHTIggWg9bHWK223eW2T5iHTe4EzRve5TzRXTwNznXBcsyhOU+0XKb2fBwvsBYFW2uN5bnVwhe93v/st7qMDGUDwpA7AOdBx7dTU87MeIXRQ4/tCrKL9nr2fvSa6Yn31Opq9Y3zhkdLgzec4ncCiL87qigEU8NCxhwbSFo5iTwYpv3zdfVFjRlv+WQI69pFTqbRrcew1tUkrhZRHMf0Ktev6horjA3BLk0tzcAi+5gJEBi2W0bb18FLHXEwnL9W7qHgvcGIKQM97nyhwFxPONmXST8+t9jQPVzM3knLP/6MyX7QOLD3sACAObNpLBj4g6vCnMiAGYPV9emRb0He0Abr+Arfy5BMIp1JYGLT3LifFo4BZ5W39zTz1yUz9CbBZR7qFwP5bSNmWi/Gnvid/o/jgSf3hrf6Mgy7006F0gBAfEpzR3TYwZWs5kfU2i76t/SHy9gYnJlImzF9JIICUyiRkRdEwcZW1D+FmyBeAxkSxeCyitg5sPKzu41h9w8d/ygJsfTmQ8S8N0OWmAoZ+HchwZQUA8gtcE3hNlvFm8ZzsugZklrO2TpwDuW/rXHPNNcve9dLm3qmQQrL8LLtgPPjZJxinnxCt5DjpKtNfdZWRL0vRie6sf5Fp/KVD+pk8Jaf6j+dtY6rOWePZz0xrn57RK98BDpTremft6zz1DgLOybBBpBSnMdSKrt707yn41QomIQXAt8f7uLV4yKo60PHg+7TqAVVdJ7ECBQNq9cVOftHJZe2ASV1y0ndfT0jZ0Ohf76UQ6lNK/zW7EM/yhZQbnac//enLql+d2sy4djPvStMWRXNPFr3AQJlbZNOLZBX95r1y+WSB95nntbW2TOoo65e85J83xKd40ls/HaRP5QFWf5PP8/Z/Wru9UJBA58Dq8KwApSQpylT+qZjRPHScgClLgg9gHQb1AAHA+Vq6MBeS/sOY8T70oQ9dwJj1FDtM8tig8WSFp4ehjsB6xo/rZDrluLZo5FZ59bVNjslVnj55ILNv+fsEoEtu6JBdfXbQ1jX+LBbxq77rxlwsX1AWiK/N+R9r1vUh4mSFvykbc7xe3OJRvC47BC9rGnuBM2ImwCTNiZqTUL117N7ebKP8uc997jLwqwFO/el/CppS9R/IvKTdd4iAyO2RAsVpMj3Haw8seD3MqW1vw2jHOgrcanVTOn05uPLcLzeZcuOH0vtsptBLAskpuXYd7xOcffuoMsqkT6eR+gwwSwcH+IOnSXNayvjUjTmt3pxf/KX4sTPLazvHGJ3q7xPXtw8CAGXbqDUP2/jcp9/T2u4Nzil8yjoFeFrnyk1kynqW+oesk6KjaSLi4x3e4R0WsLF0fZwa+HJfp2JEo1NZYHQgxa11wGQBkld5+8vGcYfr/oPa/CxI9MUWKzJN4VsQAl508G8ulNs3UrA5F+orw2/KWNvzxvGEZpZSnxYaIR7jI95dr3nAe+PWVrm8Yn3M8jVwtLnSgGd00J200XGrbvKofOr6lfZ1nvp7gZPApiuDAQM46yDWN8LR0/YQgj+rMFKcKXy3SHrEDrD8nPJ2Uoy2cQu1w7OH3asPhG7bCG6zmGiATQlMPuVVvzpi/LRIkEUu9JTpWmm0i66y5mTWU2eGSW/mX0ka//WrXWC0OMxgoWhO4085cCR/+Xha0ztpDCflz36vJE338E8n7UEd8BXwhLf6xHOLUXUuIt4LnDGE8TnZBnolwcQZMCEkgCtpv0/d9T4ul9Ctkx4e8FZJ//SIBeX2OnTpQKH+fSHB3lQdVre3TFLM3CX1k5f9aAA19oAZzRlHJ4VOaWadbWl9aTNlO0Gwrc1Z8yhpdOOvtuW7TicAoHzPY8+HSdRT1s/1DGs9m2XnSSeDjER8oZW8tvGC54v6R79zHHuBM0VGcAp5PUmzw3W6dimr8l0Kum6/z3UrPRrSrYa5a31SJCvqI9ZA1/OzQOXEstO9y5sHCbKcbqsUyCNAce06gQRuQPcgRIEyqJ9cyhdHI6stbyoPZUvhpjzV0Xadp/0hgj6TWf24DpD1Yf8cf+RgYczVrU4xngvS2pmjCe7K94nJer0FwJP+Jg+zj3ifeReR3guc3LhubE+FaaJOYzgwUNIUaALmtPaHKF8vJPGem9OHsTtpBb7c2/I8AEEpWUzl/Rcz/EXfGFNMY228Pl2ijfuihSkD7VPKyuMxOtGd9fCzBkftxbWZeVeaznPAR/TyDuINzRYjrmJtkkt9ao9/7QryLCgzr7JDxFPO6PXZUunZp7S6jVH51QhnAmfAI1DWhBJ6u9+TM/M9x5QG43PgrY7FreDA2YBTJEolBNz1noug/KpXP+LS8ZuA9Rv9Yn1MPlxrXxvXBS6u+5yBz9cLAKr7oF2TiXxfUvDgg5AySjcmaePWV/+23f/eFPAXD2dd/Bp3MkFnm+WVPwMe8Jcc9Nt8zHpnSQdKdbct2M2Jcn3UZ/01hsobyzq/duoVnrQ5gIqOcjKsvTQalWsTr8arbOqwcrzOfuXdEGEnOAObCUypKZPnVwUnjFy+T/3UTz3mHRAMOgWLRu1VTDjHja5LBMRWWtlNBh4ScG5koKsv9etPWpjXLQ7yS0/wtJqbGEDSd326fvKTn3x86POxH/uxCxDtRZ3uWqj8C7y+7mfv6QkktPTVOPQtRPfaq6OlXbdN5OH7tG0DGnPsrpNJdM8SazeVEc2Ue1d7dab8qjtpJWdl+pn1XQstWuRf3lKw+SMv2Slbl1dW/bklmvMZSOMN77/5m7+5NDPexlz7KddoX+14Jzgx0yo4AdXE9V3XmE7IrhukyWiCrObyq9cN4HkoQyitXPWDRnwk3PVE1l9tArpJmVZk/vs8fDaB+sDXnOwmTb3yxb0czUr2cHv7UnleqnYy24GQ9vGnfX22cGjjmVxBefJaMq7Lq395LXSNdeZJy58gkLctkEVKOOkn421t1nnxgE5jVCcalQNV4zLffcZF3erEg/FVtzz1hMAZ/eaWTAOgetLrtvIar/Z+tYmetmeRnXoXHU4FJ8GlTAk/wbmBTrEMUAAqdVO62iW4OZjaEC7BENoUkLoJN4E2Ma6blECLz8qjrV5tCTwlQFtf1Z8ulzL1GqvrLLkFqonj4rKWxt9Jrr2mdzPx7TOXrGiLRHxEXyw0xk/6pE9arpOdfowDb/FZ/dq4VpacXScX6bMGNDqxPGub6k2Zloc/OkJuv//7v389D6A6xknGybYFu3Ixvsih8ZNh6bWuKGtutE3e6pUvj6zwvJYTWZc35YnWDRVOBWcWk8AJJuXxtThPu6QoCcNA7M88TeMhc0/ZCJc3J5ndgPeVPY/FERpX8WlPe9pS50d+5EcWV5lCenDdQ+0mz/do0UeDWy14/zEQLhmbPwHV9bypb+KblOo2AcYXnSx4ZWvFC2hkgH4PtrfXBFSurEn+7u/+7uVtlGjrl/zQTlYUJ4Xw6pn2QnxIJ19pCj95SlHRjOfmaW41tN0WPEf87Gc/+3pFxtg4r1ew48I8BpbGNqvPPHOxXgwDj5i8xNqYT96VOTJWfTRm9JNd7esnHRVnSCrTLj0hy5mvrEV5na/saoed4GxgMYy5lGDeUG/1I0QT+8Wbp2L6vOR8fYvysSxiv1xB7p/rbvSj7ee6k0/l9nG1LY6Gj1N3QOPfzvXMq8fpeibWp0M+5VM+ZZlgIErxvbcnv4B/oUlXz0Q6uU05+l8qHRLJ90SQ90RNLBp4FMgxGebKU8IUmhJxlW0Tyqtv7dHGQ/zK035am6nw5uDN3uzNVNsZUkD040+Dxriz8SjEC/ngPR7x0MIuf/KHfm0i03hbwOXXrgVJu3jDezyTb/0ql05P6d9973vfpRvyqt6k2RmG/tJ56Rs67AQn5iaTDQJwPNZGwaWBK0Fp04rmk/+EROCsn1enWFX/5tx/unKi+ZSnPOXoSZvTNorvVNRpsDTLzHKi7ZlULysLj3/845c+TY4PZPnygODxuB6vc4sDOMRe6fKxrcDM4koDvtsX+HdP8k53utNxHd+wNalumXhZW333I71l4oF4B0D+bYP0pc0rYGj0xXcvZVMAYyMfcTJMQbmQAaOYpxCY1U/JKFGKtAz0uj+UW0ipU8bc0+bguuo7I/ym9DsrrgqNp34VTZ7aU066+gHa6mlj/H0FwTgDTyBRZ4bKk+ksm/8LtPIMx6yXbIrxqO/51k/9zHZXO70TnHNljjHAAoTeXaTkPaRtpUwoTRrQpoBolE/4TdJ6AutLPMumMKfwqoN2x+K5NpSBey0Ae0EaX9pes3nXknttgjxUwM3WzpNBTRiwo81icgcBlVvrUyRkkAVFS7i8ccEDm2v0BH2meNK5WNx1e9ge+VsqX/dnLb/kNusYT2Oe+bvSxj5pdT3729VeWQuO2BiaXx6E0LX0XGQssusQL+lQbeIHf34F+VNH8zyiUz3xpDl5Sqeq23jqs/wbIt4JzrMwROAAuA0s2ufapJzyqrtNiMqFOQnX5uz+OwUubTLQqC/CzrrPSZ55epiTNfmLTsDqxBagcq0BV6gd0AqBpomPhrLSeArQc+zJD82ZbzzRxdtUPnTjN8tqXNUpTz2BpyK0141/nkl0lNdf7ZWpW76xxOM6bn6iRxbGQH/iSx9XO8Rn/DUf8WFskz/pqwXcvcFJeaz+BoVpwm8wc6UMBClbgxc3SU1cebPOSekJ+qxQ/adEKRsaKaC+qj8VrH6i4Vp5NJxQG6t/q9Ae18HYzW52s+Mv1mvTPrr9jjE2qcDAskQzV5RbztraAqQklKd6LRzoyK+O/gJIym6haKzJQVnKqI3A8hhr+S0gymw31qHyaCpv3pJZtOTjfepBMph0Zx4afjNv1j1kGp/xFu/JGu90tQMp/eKpsR6Sj5No7Q1OK46JakKK63CbQtgHJBT1DNj1nJA1neit40BffnuMqbjoUt76pJD2vEJKZhz1GR+5TPgr/cIXvvDox3/8x4+/YDAPvIBLXX2j5dMn3/d937csAlPh5sMF8ZvSA2cnzSlK/OC3fX+8uq6efvXfN3XVF/QRDeXaatPCJi1fyIJMecmvbguEvGRMhnMe0EvZ1RNaCKV3/WNe7Rqbuhcd6iv51F9yMi/pjbLkVL2LjPcG55q5Ocg5YSbSIFMk7WbdNZ0rEUKKjUbCjh7FSbh46Kvr9ojctv5pb/XX7adSZYkuX7efRKP3NB0Orb2CuedMWVP+FgX9pvjS2vil+CwgoEw+kls0J43kyxobS9ctLmiVp13B2Br77Ev5uj4aQvFysfmTnLsWm8dt+dVBO90wrsZW+dWKd/E4eSAjPE7Zz/JDpg8KzphukjGaUkhTTIPy7xGkp0DkmySTdZ4JyhqhaVEIBN7N9MC1gx5K75s/N7nJTZZTWLd1BI9xsYYFPDQGCog3AJLn5+0UJ7To+R+bTnWdSDdh2uvfSa9DCotH9FgeaWNt8TJe+WJ89rRQMokvvPhpj35jnOBeA6a2YnwVqqdt8hb3n94chOHd3tp8OWXXxlNFjQWtuSCVj+88gvpj4Y3RouQD0q4BV3sLg7gFGR/Rqv1FxPUnxnPy0f+cy+SDp9LFF8FXNPcCpwEYWExjeAq1AeosIDYo15XLo6hWe2CeNGJ0W6zeBH913JKhWMDj6R2nrNL2hr1RIi2vn4Od+JlWrQmMNhDaR3rwgEvre7lodBjU+KqvzPd0Z0gJ5E03sbbq/9iP/dhssnWcbr9YfNyysYfVlz2xW0QA7uT30uZWj/2vj147ZQY2wb4XIPxrCqfSxmUsd9h8mQEdi5innMgLHbfO3C/2/07VVccpPR7MgzFl7WOc7OY8y29ui7Uz91Mm6q3lLu/QYc1v828epMX4ild5pYsPzdOktxc4MZhCTaIzbWU2kQJhBFLXc4DKKMtaYOqdFKKFPhdV7IS0x+q0o5SXN26oe565oBTMfUnBkzkUu4f5WaMmR3lAlZ+711f09OfBA6e1At4pVVZQv/p0y0XoPhwLlPL1UIJysmJlWSnfupWe8kh51G2sPZjhYQ2K1EMe6gCo+6xc7mRCPtriuTz84Um/hfgzJ4L7tz1N1L3bnpBCEx88FPUnINOPLDVa2xZU+Vc7rBeE0/ia4Ez3LpLnvcA5GZtAlTbwuRek3CY8QBroVLZJS7p66/x57f4lRaFkvijg1S2Ww+tXyrpn6MEGiuSBhf55rTaXNlYlRQ24PsY1AVF/KRkAVTdFZ4XnWOI9Bef6znusaKKXcohrowy/rJnAMhkjy4zf3iEFBhYS/1lQ9bVjSYUnbU5bHS5xlXkTFiFlfcCMFfXPovQnUDi/3GV5pef45OMXbS5vlpQc9PW4xz1OlSWQgV9jbbFrIUuu1VcvuZV3UXEAwxNg+l7TXDj1O8eNt/i9GjzuBGcTYyIS6kUIKjBMQehn9p8w5tM8DmQ8rTPDXKHlW8m5oP7nirq90sWF64F1CuZZX5YOTd+N1V99zkXGwwjqaA+cft1Qn/VKkxvAo218QApQfXLTYhHIupXiy31ZRIsIV9Mel3sOCJSqE91AvQYVmVZGDvhIsZL3LDfWazYPUMhr3AEK3ynylG/0KvPx5bYNWVVxrrJ54Fprt+YfjxY+8iErgYwEPOG5LUB79amTWXj1Zxrv6ZH6jW221WZbqB9l6Sbejbcxb2t3qLyd4CSUJkiHDbJJ2ZeJ3Ig5UIcDBDEFjI+U/f73v/+yhyJkVqDHxBJ6PKHZSWz3HFk8Sg9QlJ7bByjF2rrmCgv4aPyUw7iVcxPF9siUcQb1U/7y7QvVF1iv7o9yI7nTXGMAZd24pcalvjGxmMa/LehrrWT6Tqnwq23XZBhvzWWuOvrRMgcThPNwp3lAp3lLH7TzE3gt8o3LeCxoPbhhbDwAeYGY52NutANgdSyE5s7CKv3gBz94oU2eM3Sf2FjjqfLG2zyWf9ZYu4DZgVbjPSuN89bbCU5EmzDpANOA5R0ipHzrdy0JgWL4mnhfRueSUVgTTlECYMoWP/PaRAMgZZD2Y/m4m4DKGgOZN2k8i+s5W6GJjj/PClM2z/lSLuDiFj7ykY9c6pMPy1bbycN83LFHDHMnow+MxmPc5U2lev7zn7/Q9qeFTZryqN/8yGsvG50p2+oBbWOMXtdoTKU3lsYzAR2I5+KIH9f1jVbl12yss0Xojne84+Kuk7k3eMjVgZPHIs2NAyuyJGtv2NzlLnc5nruP+7iPW7YuUw9Z3a7T2WL9G2v84Dl+lO0KAXPOg/lpwdvVdt+yneBsMK0UrZqT0X0Z0L5+pFulW4E7fAEuoX9VsFyMPynDFDo+L29cJGCU700ZD7WztiYd4CkKV9fBkNXZCaVbIB625+4aMxoe0Le3Q4s7rJ40gAOpNF7RleaGStuDBUyHVvaPDk5YEQuMt2FcUy63GIQ+WTKGdz0ZUTq3fyiItk5NuYl45lqyzk6r8WMM4idt9p/+rSI5qD9BGOjMc/n4EVLCFJ8lQ9MY7eHdVpJWTj7Vx4+XDH70R390sYQAjXY6lNLrQ1/aKcOfH53wm/Xc3jEW3oY5MI/kP4NbNOlTPOcOz3qT7sxfp5OD+skpHV3XPfT1TnC2QlppMNegD8kEmlbySbtV36T7OeShFEL1CKqJTqGUS7eYZA3Q4DqKuUjRFfdcrLR/Jci6duhSvdr2KJ58rm0u2bTIwKicRa69mLV0ospKOLXlVpPrwx/+8KWe9L3udS9DOA4tglw94zYHvaeJZvdapRtHPM2+pS1MFhGLEFly8cmnPloMKTRwsFzkqK2+zYE0XvRhfF7Bk4cvMZkI0hYKsXEWayugr41gDqeFa+6Wws0f/ABu/MlnYc3zlDt+oqmONtGa4Ex/1DktBG7ejDHPtrOv0+ict3wnOBsc4gQqlDcZXQrO8ccAW400l/bjthK8+31Wx4C57iIeJiDVwaMylspqzoKlyE4UAdTKKw9gHMR0UGQ/w0prS0HV8WNl59NFHSahp5xi+oYQSyzon/UywR5X89YLMFDE+HbDnyWwxwXqhzzkIYsic+ecugJODwWw6vik7N02iof+YZLbL4CAV4cpxiRNsXr1TTlFxrM0ULuHaQEiJ+6mfGMxB/PxRABXT37f2628RWEuSuSIB/NoP+lA6FGPetSxfNKlYgXTUi0VN39muYXcfPuRIw+ie9oWVfJKvtoHohYA80HHJs36WcfkX/u2Auq0oK3rH/p6Jzh19gd/8Af/q08Mx/T/KryCjASEVlbayWcHAlmq6iGd21RcWYtH3ZsgE+E50xSR0nUK2qte8igWBRJngdzXU0bBxBaMazb7JbSABCjls0De7ZT26xaI/SlAGttcgHoSKQWiZBYfE87aqM9tZGU6eEI3vsvrdkj3NdWZliR+5NnXqe//vuAPqFlyZcbtP4irb68HfNxiaXnqkwsXnCvuyxbGa9zqAJyFwILioOsTP/ETF/mUh0auvvqB2AmuhUk5HiwG0vr+3u/93uVklhvOTS8ks+LmPODhS1/kabzJGrDSE7SuBFz1pR2PDh2/K6Gh7XnCTnBSFPuG3JAYSijn6XC2obQGz6UTik3SDIQfGGe+dCsantCi7OuAteOksQAAIABJREFUHgvJqqUcQAcMwEaxXFN8C4KHFOwrslAsLSVVT/1uF6Cb26bPTm7jdU6s8njjyqUs1VUuoJkLKe3X6S6AlJdiGxfQuMYbK2wsxsnyq5/FlxYAh4UT5Bl3aYtQC5QytNSXrm5pC0bglSfNetlX40UfLH4LSu3EytGWjs94kKdtc6UuOs3HlKsFOFmSLx3CPw9ITNboVy8dnjSWwW/5k57DgTDbNJdbmh0s6/oo2EI2xhRhLoa3VD0xS7sGRpBzYDONgAkxyR4imGWTjyZj8hL96Taix81hIUxsLhcFzNpRMFaUa5TlSSmmMlmJBXm5dtJ3vetdjxWXsjl1FNyvc1gizD1PbltjWCps/lzeHDrlUl/aPGyAV9ZTHx04OUXOorEQXFWg5IpSYDRYoawq0FowjFc5Wj7JIma5WD9pbcTocYOlWcTKuab6dS2tbfzxIlgqbWrLKqtHtu7ZkoP6DsbMA56V+wG+a/TNgfpO59HDc+NtgSJflt+8WiwLQJcOyHOo1v4ffd4IfQqc4qlTc46mXkV/5gH61QingpN1i7EJsrMw1+Brv27TgY58K177HRZNvw4c5v+kADwCpthoTgX3cbACPoGgicgSWUmnG0gBAixAcv/EPUVEeQCOgnOvnDyyVNpR5NriWx/aUqw8AGPIsuMt96sYf56mQQ/Y2r9lmdHrg9UAUH/qU1blgU6eRaO9JY9HfeBR5tc/BdbXVHYgYpUtUlk5ccCwkAFkdOLTdZ99kdY3yx1tefHnEEf/PI0Wwbd5m7c58rV8/Ng3k3/7aPWA+alPferS71u91VstZfa6H/VRH3XMC4ACH/592sZpPrkLru3D0WF56dU1m63JDPOgSZpOpZf0l56Zw3TZ7SXnIB02TlqHTp8KzjWwWp1idhdDgWeCGrgMvvYpcgppZW9lynJqn8DrL8HJr0y72lZPTElSutK5VDfZvKEij9VyWhuQ40c99FmxDh6iAewAkLLJL+Bjyq7xFldP+wBPkckGnfbdgMPycRctLKyhfn3QjKXEH+XUxo9lyg1lZeQBEx5ZPr/cSLIHaHUAXYhOMZDEHzp9JRCv3FdKqo4tgzbSytBz7f/A8ISkbReiCyzNgTw8C/FId4xTGT0A+CwlevohG1ZaHN1c34XY5k+3PfRXHTGdMn7zsfa20js0JgijFe2Ljv9Hm7b0ZACTcQKTJ6yVbEvz4yxt1BdbhWysOwCqUoIjeEG/U7mrR3BZxHhAF29+2slv9dPOik6pU46UIgByIwOvSccLBSvPKSVl46pSnnh1eIHfadHcD7WPTE74EXKb8IgX9yc/7dM+beGpk88Ui6vMyuBBX/oXO7gprwMU+dzSrFXuereDWE5KHc/66ACotmL7ah9C487qT73GlUcDgBYpWw6udgurwzMvlicvVjarayHIq9BPru+d73znxRJaFN237Av66jRGt41cs3gdwCnDPzotQvHZ3OUdscL6J++C7xy1XbAwddJtTBbhHvTwMTrBfAlAqvxJ130dIoOwFF7Qn53gBCBAAqgJsLPysgaPdugE+PZfFIEy9WaIegBor5IlRIsyrAELCNVRFnDRqK79BzDYz1AcaZPeP8Y1ucAHvB4uYE1ZqyabhXDj3k+7vtSXMlJsKziwzwMeFg0/KbE0ZclysdTo+QG9/lI0+0Z5KSD+0MuyW1BSrFxX/U/glY83dD/6oz966YtSAhd6FipWFTCNBzhbJPBlXii5engQt0dNDo0Bz8aq/lzEXLcw2ipUHz3zeve73/3oNre5zZLPWpI3aw2ULC/+zYd+LQR4NJfmEbh5CNpYhLjm6qtDRsDcQsF6khk3mgwubzwPQKU/ri1s3OMe32QI5nzSqZ7qak7lXVTYCc4sUGYesLIIrSi7GJvgnPUCTXlNln0VQa9XJfXXwoin6k73w/O3AgXJQktTBkDSH4W036nv4lxUk0pZ/bQDrA5TphsZgFvt8eqnfq4pXtqbUSZ9CPUpbWGiXOj4TTds1tUmi0+R8iQor7Lcziwn3lnV+FSHIorLIxs0nVRLGzPa8sjVNcDmcQCC9vhl9Z0Ge7pJHhfTuCm4awFYpM1v7mtjwht6ZIJX9dY//VrQ8Ea2yvXDzbSQJlvzkyuM3xYZbZVZoHKx0eg8wPikgTUPRLkgn673Mr+8jIH0RYad4NzWMeEIAW9bnXXeBLX2AUo996IA8qEPfehywtaja9xSirfuR14ua3sAFrhFA80WFf04UHC/TGjSKWXKC2hWaSu6SWINKFMAsFpTDhZrgpISUCblKbknfPDXaturXxRd3+oBXq6n/rJCb/mWb3nMHyW06qMvDhRcwfhqEcn6zgMbfQENiyUN6GiyGPpvTMpSVuORDyiNR7kfpY1nBzspMP6r43CHO6ytR+rkAyMAs6jkgg6LZiFiFQM53qYb34ET0Hvc0mKizq1udaulDV7MLfnkPeiP++0+bMDs1FoddMyhE9zcdOOwVZFvMe3zqKyp/gSnwhki80rPgHPq21LxAv6cCk5CjbkJsivhBSDnYAIcAXfcbeXvXy3Yywn6LrCcBLgOAVS+0z68mvhCrrLVnKApbGAxoe1PpDtAocC5ukBACQE2N3AqZcChlFziAj6s2HhGaypRiq5PPy4md5TiZtWqA5yzLRC2sKRkFpZ5gqmtgKf2eBQZH/rL3aXEgZylU27s6si3jySf3EILA8uPJ6DjWuJBXSeiZGEhUE7O6qAJVHksaFN8cQc56hi7PO0DFfrJA81kQh4tatrkLZgfY6NL8XyLW9ximRdtzbt9Mz4BrPk2n7Y49M8CUkwW2ggtuFMnl4IL/HMqOPfpOxCi0RsO0h2SKE855ANVYHItVFcayLPchFTZdHmlnaq2oASq9rlZv/Zu7YVMsjYpfoos3+ThDS35AVKZfAcOVmHjMeFCLro6LQCTZguAcspKKbS1YAX+FJoSp6QpNCXWr7ZZssomf6XjAW9Aayz6Vp771/5W/5SYYuLZWPAXcLXX1i/XXd+stUVAvv2gel3rB1iVxWcxHSht/ht3c6Vf7clG3fgAsICObg9bkFWyNl5zZAzqsNbmWZq8/dCQT5761k9j5DKvw9S3ddkhry8UnABEYQ22EKD6Vw0Uy/0oFqYy1pClbR9JmPN+lHpZY4JSV16Wlaumb2VcFPe+3JviFlohAyb3C28s3Hd913ctE+Zfyrs2eVbfe9zjHsubI8bRis56ceFMKuVr70rJBTEXkoK0+BSj28GMPBYTLc8As4DS6nQ6aa8EGPIoKB7E6GdJ7LFZEv35T9msIL64eFx2iua7uqxTtzzIXVngSuk72W4x0G+869ePRQO0CQyW0sKmvIM2bf30xbqRJ54BF02HN5SfS8vrAJRko465u9vd7rbMB3mw3ECkrZ8xauPg0PzyuFhN8qcfLbT6wWugzm3Gj0XLSToPwJjtLb39om+uPne4z8uwnlnODjPT64uILxScGKb8cwPdJtx+rJVO2urWs5CAUAC8XIrodVsC7ac//enHVlI5gPZlAte/8zu/s4CcFQBWkwZ83KTAFRBMNkU2eRTdHoRyyXNS2w3+XDAWhsumDuXrWeB5PzSg98WDFINSAYrnSFPiVntKhBf5lMcXHAIC97H6WRRKq35tlAMJ+eIPn+hQ1oAWDTFZ4EcayLMa0uTmHVeKzNpyKfHAFQdS5bYm2gMBYFB0C6AHAFh4rnD9odXhlcWRDPJe9Gvv2l7ZdftX7TvskbY4oR3dyrO65TswMmaLQguOxdVY5Dmldt6hPjkK9Mpck6F6QgZhubhKfy4cnAGtPWfXuRZcF6EVSTrXVZ2CdoRWmIB3QJTVDMgUAh2v+xCycgrUPS9luVlA4Yg+cFiB8TNBRhF668NEpsCsz5zYrJy8CRbXuavSggUJnWhRDmWAZOUOSKwF64Pf6GurLjmIgUKsHYXkdVAsQDAWZX4CoHPzjHe6bWSU96IeudUO766zPvLjT7qFovrF+mrcvAL8RSOrrS4e1VPfPIkBnKstLURTbNGjH97kaQ4qVxcQLRzomnP6h18WmUwsVHQvHYi+mJdmwdG2w0f6Qv/kkVN6rP5FhQsHZ0AzyDkgb4vYZ1jpekm378pQOMLMQiag2md91dn28nXAdY/MyiyYaNZPvyaHktj4p/hNLKCYRJOrLQWuX3Um4ChrhzX2SibUl+S1r560MXaAwUrjxeJhBUcTLywr60RhWCCnxq3oPU6Ip7d+67c+XiQ6BLLKc4mzoNxZjz5SJIGVEzyCqD8HY4HS4pW8WgwBm5wAHu8OlSi4+WJtWGMLCFrtFaX9LBpkgh9yljZmgDQu7qeFDk08eBADiJRpzyvhFgOll7l72EJe24q5aJDTIx7xiAVsAJd3o725FfCCttBDIwBmMeC2AuiljfegvaCM9Q/c9Eze1Q4XDk4DagOdsshrMihKt0/kB0RpgSILWc3+XVyv7yjj/1sEUi7usX2IJ0xMNqGnPE1ssTIgBEortkkCKOmUhZWhrJRevU5AlVMarqr6npMNcNwxily/aFKYlDdrkrWsHkC07+Qmy7dXDgTuJ3b7A2AokD0b60Lpb33rWy//JS2ZZwl9IaBgcTMXLX4tPkBJEQXK6Eeufuo3N7wMdO3NWHKehiejzEPnBPMUnfKTc9uHxkIm5oE8latn/H7mUr4TY4sL0JEpa2uO8iDIOwtM/mhaAGYdaSAnNzHQkqvFA98CGVq8C8oDd/LBk4Vsyq76FxFfFXAGrCbeAFkkijlPcXtgoM12sYHPlSthyefG2ouYQPm5tSZPPtBQBn22x819NQECxQYc11yk9qby5aHJpQ3Q8oCrPYxxUGD1qyMOeD/4gz+4uJgUVtva4TGXjKK0H1UHALQHZlZZXguJcQEiRZQfzWUwmz8tUnkYATULWT0xnpqf6smvbYCUF8CbM2WBfx7Y1Vab+iQffGax4zuX3iJcnsWQ/MQ+6lU+mZSeMTkI5tqCZTw8FyF9aBugHZdYUJfeyNMfkAv6pSv0pPH5BlNyXSpdhT8XDs4JJBMEZA5xsjAsktNawWs91Q+MKQ7ByOua0AK7tiwwaymPa+mwIuUl5JTAqmwyhFZc1yyslVJ7fZksbibQCOipB0CsU8ClVOoq61dZJ7adXgbWXK/qi4HdyW38We1b4QMwftzHYwEoVf2y0EKywX/plKvy8int9GQCkXqBK7DWRpk5FMxT7YHVAihoo//ma8kcfyYt2xkLlDFz5y04rm0BjD058Q54Dw7G2i5wVYGMHpm75hcf5ltbcjF/LLYtDDpAykLrq8cPA6uHVcy/BcSJ95RJQygvPS3/IuK9wDnBsWYucJnMJqQBsYgUuMOg2jbwJl0+5aodmtWR55TXiSo6Hkh2MtsKbbJYKPs5k2Sy7blMqhVWvjQl9c9y6wNNYAJs6XigFC0ouWVAlbJQCGOaCqTcAhBIWT559jnAGIjlcfN7OCArTom4cgG2cvXxgD+Lw5RJgMJ3csx6NEZlzU955rK2ATC66ACbIFZO5tr41U/tp7VdLw5oTL2JD/l4iR99pzfmS3BtYRLcipuB15U+4I/MbFcAz6LWnAVi86vMA++Cfp15dCJ8zerVstnXTCeXmXeo9F7gnIwRyJxEDBI8BSs0eVZ9yqzcyuY+XYpQXQqVkjT5yuT1M8lckBTGZEhTXgcQpePB4YNJAgpAAQI8UCb7lNy1lF9sBTWhAcn9QvlOT9FyFG+PiBeHPPIA1sTrgyuYG6svbVlCY5C2mnOhcusoh/bGNYGvrp/TRuPql7xyOV1T4pSc7FJyaf3i1S8wzOdGA1ag0qegrTZCYJd2CNb1nEN94lEov22KftG9vLGS+qEDZFOY/NTGGUOh8aRP6QdAFuLVvlraYkKeLKa505+5FfIUeCJ0wLxNfqJ5teO9wJkAMG0imvw5iCbZBJkUysHNYJ3mkzzamOQEHw0T0OTOMhMh34ksutxjbjGAUnBuTYcul65zEVm+FN5Bg+CaO+ywR30ThDfgkI8ewDl1BNJuA1AudbOmFht588da40Ub9wbV4bJ5gTo6gd5KDuQUhpuGjidulAO32yI32dwieexjH7vwTfYdunQIoyBFXSpt/lA8MhdSwuXiuj/Nj8uXvOQlx4ByrY8AQMYz4IeSk1WHXA5U9A/g9UmGgKWuBTCvwGmveSET40aHN+P0ff0VjNlvY+5k38LOOwE6CwX5Slscuan4xLtnrAN6HpF+8CPQSc8Naxvvs99taQBey2VbvfPm7QXOXYMIrBgjFPuLVlLK7qjawCgAAAiBUP4117kV/lntDCZDv5Qg14VyaMOltF/wtImJp+Ce/HF6e3mzSufSoOdwQT5rZy/Y/lQbvKHpoWiTPAEnDcQA054PwNGXD8Ta5oICl5NAgJNuH4UOHv0oSPtL/LuFoJ7PaFrJueNkRzGdkApAI48lFdwSKZBjIM0CkFlWUT3yav7UncBdyzy6+nQ41S0cYyAjbifvpDHbHzZOC5FrdSk+AAoWnk7pPRMNxKxbe3seBcCyquZGu7wYfZEzmp4o4rY63CFnix5+7N898ICO20HAZ8G1SM5TdFsOdMyBBZ7sptFp7DdEvBc4MUxBKIBBmfBCyjFdFKsY60cYBCVY7bTrpLb28lolCasVPmVDYwoRH1ZmK3EgNFEm3qod+CiAxSE3iTVy0mjyu3eXdTUmLngWFW1pdbudoU+89FNOiV0DL2+gg6DAfItb3GIpv7wBdJYTbXxpJwCO/gsBqdsf5U/5ktlsM9PJipzkiwOka/NizupHjJ6fMUTL44Gf8AmfsMgUrx4vNObkiS+ufkH75q48cRZZGm/16xqI0TZX4k6x87T0l/5MvcFjfKIj8Cq4/PSMfDuhVSaPHAR8kkF8uL6hw97gJFgCsMKbxDlYg8v0s55WfUpI4E5sU5gpBEKZCmi1V4/QU6beUu++lDZWUqBBGxgc9gCZvdx85I07ZPIFysiVE4BNvoln+dARxEDFDZYGciBuHPL0o44Vmnssr4MFC8WsG51cXis8JXRyCGj4dfLsgMseWTDulC6lJqPc2RasFIo1E6Z8mxdztA61r47y9t/Sv/d7v7fMLYtkbOZR/2hxI8nOXpxsJxDxPR8SaV5f9KIXIbuEyQ+gTZ479AGaeNTI/xQtNOb1Nf4DmrLpNdReX+kUWV7eLJaFjEvX22L8nqXetrZnydsbnDoJOCmQPANvghOswVNux9qPfvSjl1XMRCfEBKU9JcxyRk+cK2QVNfEUmXtLKeSxRNwhSiRwVSiPfYm40AfBABqQgcjNdEAGTgFYs7gsLJq5n05Ry9OGq0VRuUfd+uDm6VM79bOy/r9KtN0DFSYw5oTLT64pGGWdgdKT4VTU6qpHNsm4ufDPefXjRj9LZ8Hh4pMnfn2ojCtuy4HXxs7acLNzp6MPZBahTlYnyOhB+70WFLw2jnhNBto25sapTjTkBerquW5stRHTo+pOuc46pVtY5hahsm3xC17wgusZkm119snbC5xzAtZMpCgJXrkJ9utUrckQU54UaE0LjfqKLjomlzI4XQMark59ABW31p5FG33o148yc8eUsXoUMPdS3QCIFpc4mqzq+iCHq8RqrkGca93TPtpGR6xfQAZY48afMU6ZuG7cU6nx2JhScDLDQ9YJTcqo/Vop1SEzYNJGjJ/Sud/4zCW39xZyI9EAhvhTZoFCxyInAMYsn+CJp/LUMyahMunGF53cePnqT50JhPEYbXSqlz5qH7DF9V2b6mt7UjAnzddJdfbJ3wucZ+3YymmlbbK1I4QEkiCaAMJqUtT1WFZ1WDoBgLg97lFKs6KAStG6LaGeEzmnc/q7ZnPIBJB46cACTxQVUKTdN/VWxOWNlUcrMCoDOMonTZG7RcIqqse1nvX1wbpyXbVTX5pFVY87m5uK1+Qxxy6fR4HvwnplD7jGPQNlnSeTrKIDksZgHH48B8Ei5cRbHu/BwZTTcLJoK8Fy9mUJ2wrut325cXiYRH3ykF8ANvPX+ORLB6bqyQuYZ1V69bRLd9BCo+vAJn/2N/OVCcrrNz6uLfmfv8qNBf05nv+pcbjUhYLTABssC2HSrGr2RP7HhZArq151GzSQBkp1CbQjdPmUWB5loihO7VI4D0kDcocKLABABB4uG2vGklJCbi+3mIvql+UD3Msb5XTtAXSA1cel606DO4kEDLdVuLFcxAl+p4bA7DAil7exGpexpDit5ixEVlAdY83tsvqnyD02N2moT67PfOYzF8DhN37waYEwXiffbjF4KAI9z+06wfaoIqCSHR6cD/ixiORM5hazOTf6FJ7znOcsC6KFCk18BARj5pquFd/2JVrGmXW7luLZ/063V6toSuvDmPHQnrc5wOesOxdHdZT7AWRt0GwBkL6IcKHgxHDKRkG4kgYpmADKllLKN2lNXMKq/bQw2hIMKyBoyxq2N3IYAyTAx0pMNxVI8OJWigfjgU+gVIJ9l3bAGBDVn79c1Mq5gbnF/ectZUCaW5gbGZ2ls82f9uVz0isrbryuk0tlMwYCMiVD8rE4+VmQyMTY8crS4QN/yttmyGux46IW7nnPex7PY/NTmXi9iFoAtNdfoXl23SIzQSCfDAJy3oD8k8IEh7bJcOanN/hO99Cb12s+5qKoLpnvkrs6FxEuFJwdr1MAK6n7UNwl9zw7dDEok5uAmhz5ncYSjFU8oRM494nLBpDoO1iiXLmagQBIunfGneTacc3ksSysARfM3hLoup2hfVaWQgOXNjwAlhU/WdceGnB/FD9W6NxkdIxVrIz34GR2hsY19zDGTCadWLp2kEYBKTqL1N7K6aP+HC550Zxrij8LUxZe/73hIW0PiR8uvFhdn6fU1r1WdMhV2kL33Oc+d7GmgE1eeDZXFD5QGBPg4TWQk4UADPjP0rv2E8wdV3kNiqVwx5/Ahs60tnMh0HzSDazqJHd0yBqdqYtzXJMN+dqw1PEwyw+VvlBwYpIS9TaBFZqF85SLQfW/Jk1mE5VA5BXQEKzG3GEC5HYRsGN+Vst/twIgikfhABC4gMGNcFbCjW+LhPut9qcsL8VzyqoeBXUrJIADZTfW3WvLOupj/QNq7cvPqgZ2lotLy5q87du+7TKeFJViUQ4P7HN98YQWPixoaLLAFgV8e9yv19bQ67aNehaMbqwbE5ea3H1+5VnPetZCC3AB1aJhcQJU8rIQeBhA/0B5eePONw/KzI2tw0mhusrVbYFqnM2j8hZh4w4w8rOqE1DydwW642exSn+qH2iVRbsy/K7z4oVu4a3QYqSNPsTP3/yn8cZWvUPGFw5Ovj5F9SNACgQcgn9J1yS5Vt51K1LWQTlB5ga6tiqjZwKAD5hc90OjtFUOUCgdcOfa9RqZtllCIA9U2s8TW4BXrj9l6rkxL80CtadEf4KGFVKHHJRNRW4Fr69cYdd9Wa6xtXAo64cn9bL0PACgBUJ1BDzP02yehzL8x5v65CM/YOHFYVQHUik7xTVXFjhj6d/aTwDql5vPzU3p5QW8PCt5gYosSss/S0hnvF6W1Zz9mW8hulP28u27BYu//mvbvCijmxOs8oxV/kWFCwVnQjPZXEIHLlZjbhH3qWPxefpowAmYMBIogZUGeMBzOGTigYpi9gI3t9G9zqwP1471pmB4AWpWRdoPoNBgtbKOgAZILGbKyyJlHdEPfKxJwA4g0Rbf/OY3X6we+q6FFiLjoASUHJ/RsU8GHHxmCXkdDnHQMEaWFL/caYc88p28BkKPrLGI8vHLWpKDdvbW5MBKqh8PHpEDUod2fkBq+8AlFZyKr61NC+lSYfMHGNAzf+aazIw3UEwlN6eBoHzza/twWggYxb6IELDWPLYQWHws1HQT37XVV3q3TruOd2lh1r025/B/LxSc2CWkVnuTLpjwTl0DnBV5CoDQmvRWPnsyytF+lTtGybIQlJtCc025r1xALivFpaROUylq/LBGpeUDW+BDBzgptJg1Crho+2nTJ0SUA1H7T6ejXET0uLH6wSeXG0gbQxYK76wdmhYyIFUfTSCzsDlVZemt8OpZCC5vFjtjtEBYZNBR1j437wJfPVOKbjIzD3hUXz/oWfDUNQZWHo/yKbRFw4MdYsFtrgIXL2UPcD3UYC66rROAtKMfzbM4HViDqz5mXF/y6k86o4BW+emZBaA8dYUWhfSsuuhL97u29rUnv/5befXKP3R8EHAm7IQ1BymPsrjfZ8WiUAKByJ91CS2Xp4FPAZs8+QmTJdQGHcDJagEK4GXZlK9/AU1dZYABhKXRqkxeINZ/AKYEPWSgDn4q03c0c0nj0aKivsBCy7cYyPPL5Y6HxqVMuuv22OWL68tYGo9+ArS0engT1LHACfamFg508UW21cuttW+fYe650oOp/ObM+YBFRX7blE5jWUnBPKvb3E7LVF701TtLiA/1c8e1Kx2It9GqD/qZLs56PI6LDnuDM2FjFBAbcEA1MMrgl7VYDypAyrdiNhkJJQCbHBMtXN6s5NwxIaA5JKFsrEKP8OmXq2ePyEVkFdzScTJJkVkAlhX4UmxWq3QACHS5nepTXPRZHJahtzUCT+Wsq68nqAvwnUK71q76LKA8ctIWSHNj5aPjZFN9YOstHDHLybp6iAL4gQlfXGFp5QI62ra37FE842XVWViK6SDJtblwKNVnP7mbtiPc8D5Bak56n3TOe2DS7yd/8icvY5UuBJLalB9gzbuy9KBydNOz8rbFa920ZdJuTU9b/SgL0MWBNPqTpoUp3az8kPFe4Mz1SMgxxkIKlVM0DwVYjSneve9970XJrI6tkNrk0mib8KNl79I+5JrNkz5WXopln0HhKJUAmAKQ+myievokSArJMqgDIGh6hw8dz5pyfR/5yEcu7U0OfjzL61Djh3/4h49fH2M9uMjGZZGg7Lmn9n/40UdpdT/+4z9+yafU+FEOfNxmVtYCw1UGXqCyoKjTQw72gugGZGn9WyxhrDuRAAAgAElEQVS062BLvp+9JcBdus5dVhfY9M9dNQb19GFxMg4gBm4LgkXLtcXD2Bx6UWBuslthQOsEV9w8E1xyW4S4+aO8ObZPdtbgmtIrE+jPBIyyeW0egKB4aXTGP8AU2GsS8Ob1tkWgMxHj0zedtPdu0fGPnadhid6h4r3ASYAJnoBj1AS24rSyUATgFAii0EC7FhOEED3pvroNXEBUQN+pb0rpZLVbJfIAWkypKT6Fm6evyiisWKDQgC2wQMbYCWR8pThNMoDn9qKT1WVtO72VDyDifoHLdRaawpauHqvP7Q0s6LKSud0AFNjIvvFoD2T6ccvENZ615UEYD9rq6xcIBfyjI2gjAKw5Jf8eWlgKrvuztiIUOddVFf02ntlOmg7Ud2+MyEcj/Wmxli8E7Guvtv9NNyt1PXXPePDVfFZPfkZhHlZWXmx8k175h4r3AicmUtgYIoCE0gC5PBTq8mZ1NhHeeLCiJfBiNAy2dgGX8PqEoToeMQNArpJ8isbSzD1meziWZRtwKEogVd4Bj7xcWHVYNorK+nGLc6FZG1aHBU7p3HboQMgnGIFc2aWN9UKT0jsp1QeryUKq73E5tLmeeOGes3KA0ytoAMHi+ekXXW4wlxI9Vql8dYBSnfa3lF8/FilAMxdAyyL74c2iZwGl+GgBNB7EZMxFtpVwiATQ3Fp7L8psTjvJFc8QSM0VnvR7zcb70c/Un+mBTWsMoO7Ruo0WGNKx2c+udKe16LaoFs92xmKhcQ8Tn/HRI3/VjY+uLyLeC5wGF/Os3EmrmQGbDCeAVvlWKit47U1SFspAmzQuifZcT4ErIeiLAgsE5aFrE++dyiwXt1Yehe9/oXCvKS6wAA1lba9HyQHGHour2o1+1o/Co9WPddMW+C0KfcIxV1Y9p679H5WeZnL4QrG9ptXBz02uex1tWtmArV+HTuRmvOgCWXy4XwnwHjIIwMqAUj7QG8t8fc1DGeYD2Cxy+BCAlnXGB0tM5kDp5QFgFbQD4ObNwmo+AxYaQq6qBVa5etxh4LbA6UdIF3I9ATA9olMBqDxt9O1jbmcJdCovIIDawkyDgI5+4oU+aaefxlkd8fToXF9U2AucMTUHaoAGV55JsvJZ4bNggXBurpuEaM6Vycpbm1xj9eyruB0AyTKYBIpJGSlVCpxL18lqip+FzKoBmzZAWttcR6to7RuHOtESA568QJYlv7yxUgVpdbbRAlr3VXNfAR/g4gX9vgIPrB3qRF89eQBSOjmw6ll9baMJmO7jGqe5sg3oBXTAVc9CSYYAYr8soNWJJdrrYP4moObDI4BoH2/RbV7X7XNn5dMNPKQTrlsM1u22XesnfVQencAob61/8gT587ALWOMH3Unj2haH+7sXOAkssExhJog5OTbSVnJWy6peyHUtTkgG7dckVK4dK0mR3SRXBx/oO6ENLCkfdw/oAlnWh9vLqqgHzMAnjUcxgLD0XE11u3eqTD/KAg5w51J6kbqv/AGBCXQI0grcs7L2boDjjRg84yve4hVP3GqurwXBWHwfCb+8A1ZVH8ChHp55A8ZAPsp5Atpq41TXAoYe19RYeAd4kc+644fH4fMuZIoOt/cZz3jGMmWd0HIr3e/MZc1CqtQcSsu/ZmNthZlvm5A3pIw1mjqkbjqQ7FwL5vssYV1vLgTmZYb0qD7E9HfyHB+1re6kc8j03uCczExmpQ2sgajHXWQNTFa3E6YAW9HU1TZAqt9+Rpl3Cy0KlIni9zmPDkUoqD1olhHA7J0oI6WgzNJ+Hb6om9JzRyvHb3XkWViysK6zopc3FhGNnoUFuG7Qc+caGwWh9IAE0PhEB/AAjAfAI8CnPaDFrDpigLMo4LGFxPhYNHTQ6H+K9ABDwGb98ClfW+O1QGhL3rwbcsYbngFWG3PEwrbokj3em2NzIh24ANYe1NwbqwVEH+LqWKQscOgXlDXnExTK06WpY7U7KZ66pc5sW7q9a9fRis/aGcuap+peVLwXONcDmkzOMmmHPNw8q9Ec+GxDmLUL1Oo2Meqm5NLqNgEUU5ueRXXtd4tb3OIYaK5zfSunuLmjLKT7ef1LOgoFIOq6N1o+cLAo8i0InQi7tqfi1oqnh4A3K2+nkvg3Lm0AOZczC16snJXkalNkdV3rv7EAWI8YxhP6+uI+OukGONfo4FlQ9/IGrNxgYzcudMiUNSUXwdhZUgEws5b459kEKGNEs8XPmOY4lLWY4bkyAGm+9dH+c30CrKyQnnS9Ld5VR5n5eNjDHrbE+q/fdOyk9nQSbxcd9gJnzBkYhhuUfHkGH3hYuVb3J23uL5ZvNU4I8kqLmzB0Ugi0KZfrlJ8SWYlb6SmBHwVzqsp9paTyXFNQVsgJbQry5m/+5seWtvbFrO4aPJVlnYHG4uO602a8Ul5egocH8MuNFO51r3sdH0RRePQc0IiB28ESy+b/d+KTd5D8WFPWUZ8smvGzvNo6ZOMek5GYK8vSR5vc0LF4ADhLyaIJ5OWASVuAVAawgB2g1cvrSf7y+hcYycUDGawrHrnF9tj65Waroy1L3b3rFuwXv/jFyC2LxLb7iPSi31LxDH9O0k9N2wuvrWJ9FM9uuOAdTM78Q6f3BqdBcdUMklICqAGtB3vNxjU1Ke5JmnRgFaovPQUhLeR2SANyq7Rr+x97J64nYAK3VZvrB0wOivTJ7QuE7esoPLdKvnJupLqUHDis7JRaPvCoXz/oAyzweEgADVZJvT7ngf+5x+Hi8hrU4/q6qW9B8dTPdJ3xT6k9wYSf+X9ZLCqdBuNHGUtkD8lN1fYt3uItjh9csH/8gR/4gYXOdCE9/YNXoFQHwAEV6DttZaU9FwuYHkywv5Q2b3NOvIdJ1hYB9OyX8Yb3fm0pyNnJODmQ66XN9kNwsER3otscW0ha8MnT/K71aiGw488u/cRHIZe964yHazSm4cDTNBa1OXS8NzgxZJAUsdUvJgk7QcszSVaxBF69GSeErGZCc82CCmiiYXVXrg2g1JaLRjEIVWz1NrmsWooiP2t4eePaue77qNJ+gNSJq1W+vSclrI5Ymb7waL84J71JBCIy6oRVO3SyvCwjPgBVmSd+gFHawkPpgce1AMA+R2lRtDhoRxbKjVGQ78QVX2RCRk63xeShXABIwMa32DzirTlgPVv8OqE1B/e5z32OT6a52h1koSGdfIG6MmMiKzSbJ+UFfSbL8sTmVn4B/2cNJ+mn9s9+9rOPyTRX6ezsQ994uJphL3BO5tdMA0/C5MIQkJerAaDVWTkAB0A0tgmgo2zlPqnJheKWoeNAyCqfQFkEhxmUgcKkAECWdZQfCCgznuRJtycqlseKBiL5aLrOVRbbqzn8YGW4cYI8Su6+Wi4g/gQAYfGc/KIJKMCJtgObDpaUGx8+WLxOmPXP8sgXO022eEzwSyeDazaeC8vVwgLo3GEgYTXFaHCL1XHtrRr0ve/oU6J4RwfgPRXVflxaWzwZhzYdSrHYrvExLSqa8s2DRRAw0hfy6ZRemp6tdW0ugOpsC+s2s842A9FiFO3i2m3jo7KLiPcCpwFuE4C8AEfg+fV9SoQCCCbE84utWOomIOVZSmnBht0N8SaREgnaABCAUnDKTFFYTMqcUtjz9HA6YFCOm970pgtAnHICCQD3UAIXl9LZL1Fs9T08QBm5pCymwCLGC3B2k7pxqfOoRz1KtCw+bgEZm5glmgtB1plSW6i4sfhvv8ktZ2kCGYAAksXK2NXDl4cijMVCMcvs8eIbP27NOPktPOYxj1mSaArG4OsTbUMA2eJHFvPUOssov/u8AFlafqfOrKd/68Cy6gf9wNIiy3qb1/SreGFq82fqSXnr+DT9fP7mKSDB/fa1rslf9xEP4nWZ+ocOe4FzMoPZtTDWVpAipnwBzArZxKAnrSxByHOd8lvxhdr8v/buJ1Wy49jj+Ao0fxrYHgk09dCeaAuaSEYgPJCgt9HrMPTUYJC28Og1CIRBQnLLXsmrz3F/2+Hz6tatv31vlSqg7smTJzMyMjJ+GZF5/tzCLLNvxHgznMJS10wYEzBAxmj8ZkgrLJOXF8BLGOmHtNXg8IhAgXhyxovUL3xMdvnAE3jxUz8ZTFrSQkhH7QKWNH0ESN5GvsnH7O4YD7JJ04/28cdHWh3ltZNXKGJgnHSlDXn0jIeJg6fEVzv0zbsrQ89NLIAmjU+yONZ2upSXtzShOp9jHTjpauazJfLMPGX2pW32qW52JN2yrLWvPKRN5aY9HyvHvznu9/ds4HyoOZ3IEJQxGAZWfgANMJWr4xOkrUvklQYERiPPsV3EBl2eEJFRBiYyAIg6do2lbXzwtsAq1AMOwHGdcfNOPCUySMLXaSg2S+Jnc8U2u91RdQ34vNluw0hZfSQfj0wfvLV+0Q85gEBaH10zYfA2ha3AZqIDBv2zCwpEPKvNITrwyJ61rDUofuqYSFzXP+0LP/Ok8slsEgNS40EGpCyg4dvyQF9dpx8yAq+6QKpfyHVyAT4ejZ2QXxQE6AFSX4q4soGOeNFbNMezvFs7Xhycc7bxnRnPhQpv5uxkUConjbrnJC2vwXAU6hkou7UNmI9Lv96sh5AvBrSrKTysrvC6dpoI5o5qMycDUY5hAOHauydjvOb6KOMiV5MOmdY85PFgDNordOQV4jH4nuRh2IAAfNIAbw0KJIw7ADPyzz77bAGe655Sck04/P333y9lrVfpXX+s2U02Qn8TiU0s/E0iAEQP5DBJ2UXlRfOoygExUEn3Sps0QDYx8pRCas8Nz/WzZYY2moym/umkcXGkQ2MXQNO3cuVJ3ypdFJyUmUJTOmMwkGgquOuMpweUgUCZAKiOPF5uUqByTXsGnzdC2jIzBxp5lcdXfnIEYmUQWSYpy5jUmzyUmfzzBLNu6e6PCW2tX9uR5dV4SfK2o9xupzUvcs0PoIWGM2TvmuNc/5WvvjrO6UfdJhkbPfQGcK4hEYSxsmZ0/zOP7Vo8TRpzTfmb3/zm3TWemZzKCvd5UzvQsz4gI3qfY5QtuNbYSP/a6KLgzNht3+cJ5Qm9AMyACEXXhq5M3ihw9zC2ARJGIsbc4PW+p/Jm+cIq3sKzuAiwKr9kjD8BMVk6V2cay6jybmYPmOpm8CIDbTHwKJ5CO2DkuRhvRiw0ZcBASX7ej+fkqXhNIbowXD08AAmgeCjhKE/nSLeuA4+juryyNpHJxb1a1xEZ6YxXA0J9sAuO8Hy5CYU/+uijd/I2aZgAyd9RmsfsnHwTvO00K8cG6Gu+L5m9zBciyECPjZtjNuHaLdNFwUlxhXYZvTxG5yZ8lEE7L115A7EeDDe+AQaAfbdWGx5s8DPADM1MjRg2YzD7Rw10Hq62uu4Y4Hx4mpdTJ3ABnnYCbUdlCtMyNLxcx0+/vYtqRzdA8lrCRrcthLmAZQ3IsAHKQwrApw+eLhL+ksfuqTyPFAIZnsAnJOYVTVxC+sJOIa4daWSnmmfMc8mjY48udusDSIHyxYsXyzuz5AB8E4QJz6RAFrvdeAmDtZvu9dXPRGJNSjfk/fLLL99NCtpdU2NCf+mQ7tI9ObeN15rPLZxfHJztTFJW3tMAGigDYWZHecoGxGAaFIZdnnO/V69eLXXVw782qsOo8UfqCxMLDZ0baD/l/VC3e5aT8WfmaxvhgZJ5pnklkwW+8zG+pcLmD7mAIu/S0TrSNb++Kdt5O9zOe28UEJA868+8MJAAt/y++2OiMjnxggzbhEAG/SDj9O6Fr7xjZMLAbx0uN8HMnVjlkH5p13mhu/o2tZpss4cm5CY29RsnaWNVHed3cNLCGSgD7oilGdm/C48Ktwpnmj2bLZWbg9P/1nSf0M1sYORJ7LoaVAYmLOwen3t7Nl0YKPCggNbGVP9YKaAro2yG43zKBXwZk/Qsx3jir56+M0QhacYPcLzZJ5sHCMjPuwj1gMZjebwhoAlrgYkndd/Vt3l5KmWt65Th7YSMSB5QasvmG+Bqn8fzPSR94vl4VjR1TP822YTBQAXM9GnN6KVxMsj3lYdCW+ExENoZbp3p+WXeGRj1UX319BU/1Himf3nZiMlYucbKsUlUetukp/6t0UU951TwNFa3IgwWr9ltiTlIayUHggyJERgkPN0QR2Z3YS3iORgM0FufMjprHwYrDx/tGvCMhIeM/wQofhN4GZf8qL6pn4HZQSUbQ+oJIoBrl1P/TSC8DkA6t2FTWsioPAMHCqQMo9cPtycAD0gc6cR19SsrzwTGKyP6LjTtnxBv64+yJlAPYNjJLYQW8ZBLeKytvLU04GmHPNJAKV//TDzS5EEmL7ovInIsTZ702dg4L09U8o/NwwPZxMLwRv+cDZzAQsHNcPRFuSk4/TUQBo3hFXq5PkHgfA5ARi+fYdZOg2ZQGRSy1mHoZGKMeTxGrV0y5DkmEAvvktlR2SlXa2j5qPY7ahMxZB7ROcMMdNLkcDRRWG8yauvN1pbqVx5AeTDlpZWT9gt00gAsfBcdODcJvNzow4Shz3RW3QCsnV3EY+Olbg9mGIceW0xG7eZVhbpkcKQT9RF9GbP0s6vdfa/N8LYxU7dxe4yPcc2OKkvOeHWU13jHv/KXPJ4ETsY8FTQFXXd6ekZKYTyMS1g2O/7Pf/5zslnWbwHCYNsMsvmBv18PHvCQvRGCZ4bLoH2dW1jJA7jpDrzuswUo4J3gL7zuuqNfIK8v8vI8jC6gA4GJhcG+fOuBWlvyIkJB+TxJu6vuzVprAqzH6VqXe7jffUJkE83zyeQXHosQtGsd2qth+vj5558vsghlAYyutSUtovBwxdT5fyl8nCijTUAjM6DRrX6ZVD7ZeMhCYIB0j9VEwrtrE3idGzOUPhl9OhzNHZVkA3hNO9wXnDVoApuThvrZXGXYbPKXd+njSeB87H07Hcp4KVGnU+K33367DLa1E2DNLXWdbl0RIChmrRw8vXHPM1ROe4yVsTNGxu9heV6M4butAhg+cmUNx3gANmBpe24CGfgMubBXmcguKwImsggxeRoyMWa/Xl1Tzjnw2SQp9JMnihAu4mNNyMB5UjJaw+mLCQXIeF7g4P2BAlisvZXxU09/lTNhmSyEt6IU9VD6Wk52/KEX4beHFvT/9evXSx+smemWnr3g3i6vSQhI/Sc519G6rcZ2R7NHXzIpZmOPMWE/JuXsqnGWZ0Inv38aPEnZbXYwy5wrfRI4zS4JGvjmDERIYJEHmGgqzpqFZ2NEiMdKUUvG+JPirJsabOCPPPIGdMgGRBsv1bMWyjArE3i8SKw+qj/rmTOD0mZAri9encILj3hqr7WWPKBxJGNhocGXp01pO7B0FQ/yAIG+IPmAj3hPQEAzlFQmUEjzfCIcff/444//31tAC4MH/hRNWM+Tow+pmRSAAP9CZZNEu7KNtX6Vbsw0ZcJjL6cS/eNrbKbd0GHjfkgb057W46+tHM0hPE8pexI4Z8MGYQKT8jN05Rpo+cpRJgUa4N7kYFRTsYU+KaoBoKjWjOoCl3ptzXt8jbdBQEE2P+EV4wYuj7AJ73jOtvzJIhQUGvI8PRNLDi91uzHfFwJ4SGGb+6iA2CNwePCCjryJ9kQH2pFncrEDa00sFOVtpcnJswnHhYpArLyJpq8HmMRcJxs+dkh5TX3l/QEFaLVPZ/TpW7F2d/Hy6lrUZNP5tmPA8jYR3eNhV1if6czmEH1pR/+UmWOOJxCrj0QkgXICYbl44p9jwMP+gFs/OQb3tIvgyHlu8B/axbOAU0dSegKYZQKVvGayQClP5w2q2wMZgnwKC4gBfvJiANp7vQmxEN7Cth9++GFJ+96NnVueDNDcYmG4AVp4yxsIXRyBGyDyAowQ4Bw/2ayr7PS2Mym/kFW+EFU5fNyoByS3MHgS+fpnvSbfes0zrsJToJIP1Oq6teSaOsAroiCvCcCtIDLj0c6siaM29LW+CSlNPDyl8l5V8/UJ4KXjQ2d/Y1GkQM+AaJ0vvwcqjIHJ11g1jtpRBvU+rvND218YPPCHLOcMO5P3geaW7EPC5l189rl2EjgNVqDsWKOB0TmP1qA5By4DCYCM1+aB80I2ZRAefVPGeQC1Loua6Sit2RgfO4gMJoUzepMBL/Lb3/723Tt88oFSWXIBAc8kHxB5rjwhvkJJ7Vv7mW2V+8tf/rKUsdZD8lzHy+N45AY2YauH/wt/hb2er6Ubb48AHiKPthEDxI+n+5+3H5927kcWetcO/voPpK4hfIBfXWXoOHDM8VgKP/AHMNVD6XddtKio/OmVa8f4RMaksSzv1CPZmtD35WW8p51WT159ol+RE9uJ9Glbva6f63gSOCcgCZxHS7g+Ddm5DgWW6hokhuNXnmNpdasjbQBswjDkFKRt9xS75ymM5DXw4K14Ft5JeCU8BTL3Of1evl2nChmFlvgzcGneCTgadGBi3PLUc1RGKMlTue6bPF3nxQBZ+7ytOiYislgn2hDiPV2zw2r3VYgLdOQPhDwq+YSv9ISnCcQEoIzQstsawnxppK82mZRFgYu+pn6Xi1v+BGSXAhOdq486Ng7xB2a/9LYUfvuHjZyLZvvJgHf5h7STzPocrzUg44d/Zcq7xPEkcJ5DIDNUs73wbdvgNegp/SHFtEYFgoDKUBkJ5QMJAuzWQUJaxo93t1/slhoYIOpTHfgoRz7eVOgI+NZfyvNc2gUEILMe85O22+kaUAEPgMm3bpSHt59JQ7jrAQZHeYjcygEzkOqnMnZ01UHSIhRtonRq/a3/5A5sgPmQDpfK488sV3g7+SiqzJxAG6/B5mJJ45qMTSAa6yGLizX8Hhg/OTgZCmC0KcMbIAbQzCttECYxACEiEkZlHI7CUOGrOnOHlodj8PgBqDLIERART+T5TwRovKDBBwIAwd+tGqBGlQXmPG5hJUDY4exFaetWPF3v9gqAo/LsikoHLmny8aYA65yu6InM0o5AK+y16QL4yvHkPVixNLL5U7gWwMrfdjQu9JxuTV7dZhLSC5vn20L0rc+N2zae58zTnn5oc5JP37TDPfOvLf2k4CxsYARAygPxJojCmwkzDoPR/0xcD4idVGEcXgxz/qMbvLX1erOBlOHwPLwnkLqWx8mjAjzvK2REXuYW6uJvncyLAT6wAQ9wAA+w+QlpeUh5brXY5QUi57wssOMD8M55PvKR3YYSj+w6/nSCv/aAUl2y4GlTSHhuUy2PpS/q8NJoAjSdLxf2+EN3KFBLx6M8Y1Hbrqdj6fdB2jMuflG20/k1Hp8UnFNhgc1abD7SV6jKIDIKnkya0QEsMjDx4B2t2ZCQkIF5tco/wJU223oYQZrBA7UdSGn5AMBjWjMDE5B5INxsrG27v27DAI467Y7i0b8nBFAPBtjwca8RoNwHtKtstzYwW3NqQ3tNENaJAKuPNrZ4fH1T1qRADrvQ+ijfTjO+yJq391fbLKOb6SnT6VLhkT9CWSDEI12vwYd317BrMn2E9cmXJxiljY3frdCTgxPAWstQKiP2sS1HA+43B2F6AeVda+Z0zqB5HwCLL+M3aLxNpF5eWp5H5yqPnzSjn+HRV199tVQnm3zgfrlZSwojbfQgYSYiQyGvkDSSr07G3DoXOBm163ibEPAEsB5awEPbyiB9tIGkb/iZ2NQF7CggAligapKrzEPHuesaH32uvZYV6pskmhydK3NpIgsylunTOVmnJ5d3jfSk4Jzb6xkMUPBIjDBvQPGtbaQbiIyhz5pkEEJFoV4Ub+fKCgUjhs7jMV5pXsDGFM+mHc+yAjFvbA0n5ARygEQA4pofvjyptDpCbbcylPUABFACnfWkMsqSU566vC3ZhdaOQm6e3xHZreWlkesee2SE+k0O7VQ23fZgBmAy5jxohr0w2/FHvYBJj3SyruvctcZjB7uzX8oWmnjO3sATMnxScOo3w8pjTRAxXgQw3ZLJsBieQZkze8YIOIDNWFFPxRg8mxgRQK4JWFCbPdL9N2Zp4MlrmUAYI4/HWwEB8GqfB7RZUlnytHb9ZPNQg3N9wQNg3eOURupYm7ZLLDQGOvnWycDnHqi+S9tAogsTirZRhtpktWS+/ROAKjOvrdPrKAUIAyY++FvbBRD1nTdOa37nPl9PCNrVL7rZ1vdzt39pfk8KTt4qQFImxQpRymN8QkKehsEziAZeOdS6ioFUD0h4owwRUEszLt4G+OM1jVBZgEMAoW2hpzq8lXuSeDkigAiEgIav60JpZchEFh7UTid+gKsMfu0YAz45rEvb/BGy5uXt+JJBqF17+kI/JpUmODKlk9Z+6kkHokM3S+gpXvQeQLUl7ac/ftH7Akdjro/7TDjJdw3HJwXnPgpi2J4hLcQ1CEiolcFkHPHzipW3KBqs6rouHyhsAqlnArDB40sIgUK4KCzlXQOxDSC7nwzcBo86gGxjJo8L1MoxGM/VaguY7EJrC0/tmTwAzAMMnhYySdkkko+sGT1IgQrxpU0E2qMDXpReeFl1A0OTlvZQR+nAqT3100+3R5RxDcVn6jhelVkKnvCnNmIRf+cz3fVtRxNCZfWvPm4re2ge/cRb3WwvnRzK79Dyzx6cwlW7jz5uxaCFmZPmALvNYpa369nX4xosXgmvgGpQu+aWifAXOA2GsBMo8bbmY/jCRiBjmHZJAc3EwUMCoNsleU6Ac93tHDKbDJT14yGBXhnrUDux0oCXl1SXbB4HJNvrzS0Wmz3WpwCNTECA6V8EBhay63+RALn9pkdTNyBLTy/KGIXT8au+cnSRcaY3+afQNPw1n13X1mXnefYw+zivH5LGixx45aFbfx/C59iyzxqcrSN1jjfpXybMtSbFzbWksgDBC20boGmMQswGM4NTxxpSSMmoX25CVfykeUogAcbWiIAsTC1E5j2VRwbUz79xN9syevV4T33QjnuZypgY9FfdQma7tdaX2hDuCl0BSBnykb2+F8ouDW/+zNldn/SbofkBWcafsTkH6rxpxhg/ddKVspN/ZY49kk97cxLZNnZr/srQafWMYeNY/9Z1jjKtKhwAAA/rSURBVDkPpNrBd62bY3juU+dZg1MHmq0dgcB9vv4BrdASUVpG5dE66zAeD7VbScF48EQZmY0m4OCZeVrgc5+SZ+PlEC/GCLTNuwEhECmrjLLdU1XWI36IZ5PvFk3XX26AztOqB3jCZJs9JgmA/fvf/754S2Wc25jyShnPSQbt90mQpZHNnwmSjCbPWT+VzWir5wiY+PoxuhmVONfPyWOmJ59T0uTSjtDahBUAtsm7bsfEZPddfeX1Y596az4Pnb958+bdJZMA/XrwQxvZ27sCF0g8e3BmaPpuABkrUPIe1nR5rGZP5TydAygZqzLT2zqfygVaxgioDBRAAQZg+0QIsHs4whsorzdg4SEBSAgNuEAmfP3666+JsIDQOpYB8Zbke7kBZ18paL0qzDXYAOnHm3opGvH+Jhdt669NITwAcvbXVwci/UBFCHlGefpcyFo5fKw/GXj6oo8JenUj5YHgnEBtwqv92nrsSG9kDZD6VJqM56JsLH7prvNLHZ81OFNKCqcERoQoyDO0wj6GixqQzqsfMAGux/+WCps/eVb3UdWbO7UBuK/Jq6MMwwwc1pqTfB9XGevINoqE5EDiKSVGb/2ajNrTjjUuz4ivCcCkVL+FsMgas7zAgZ88PNINg10Tw5+AA954KJvBBeqZlx7lVSc55B1Ltbmtfvrddm3mJU95yZUtlH/MMT1qo4nDC9loX/mOabc6zxqcKZ6iKWd6UR3gOYWmPJNH24ABCDwAnjeZSsyI1cWzAcybyDcgvdHAQ/YwA+P3wDuD4ml4Mx6zR//Ix1v3VJBw166v0NR60v1K13hD4SxZ7by6lcJj93igDSL9Blo8RQHADbgRECozvWLX1NFPQKzvyk5gBjb5gbFJKj54ixwyUPnqzfPKHnsk3zaAymtifIw3mfQD6XfgfKzeMdfjrc1tch/Dc1edZw3OFNBAGcwMixGiBublJtz7ZHODv7c6gKr6lDqNqrpd75ih4osfsh7l1ZCPWfO+gGnXF2i0ryzQacduqpDVLRWhLgJEEwkCWkAzoQClMspbC6uDgAIoRQXAH8jooTQ+yARDHtdmH12rX9Uhq3ZNAIi8nkbqenqOT/mAPScwkQTZz0n6ob1k3pd3E6zy+pM97Ft/V7kpC9n8tPG+6OLgNLBTgdKz0+uOHjpIlKUNhvXyLaCEjLwVyuDwTY4A7noeJYPsWmXLV5bHaidVuzM0LaQERNeAAGk/cCvvug0haeV437yWNpM93guTI//gj+hbvzqX1wQlfU7SFoDMth7ib82OGH3y0EFj5tq0lcmz8VHmVumi4GSw7aZRYAOXMp1T8lT0HIzKPXRssBpYg2zTqM80MnBA4B0CXfzVATyG1GzbMS+HPw9ZOy834PekD168JmAJq3k6JFzt27k8dx5KuKsOkLbDrHzfc5XmockN/OSuT66dSkJUD6kbCzo6J80xpKf0u08bgbDjtANjg5+8eDY+eJe3TzvXWuai4KRc4dA0iKlgSmsAjlEgXoGu+u4Jfvrpp+9CROs84WIvc1sv2lUtLKxeR/KgBp/8ABmQbcrUJi+InJsEyOOjYSYlAPeQeptRbu4zQmFvgLdp5P+iAOMfNh/16htE00iXBk78g59+TMDXzxNZL9X1ez2uh/ClP7JlJ+kXj8bhEH63Uvai4NymJEZB4dMAnfsZHIPUTLqt/jpvPlP65u19Kc/C4jE3TJwDgdsRyE4vIg9vq+2Mg2zT2Dq3roy6+a99t0Pq03xWdsqGN552ak0OZCSP89nff2z+D8gEUe0dc6w/2+rOcH3b9X3y9HkbpYtt12belGHqoAmtsvjVluMcm8rc4vHi4KT0FBswKVLePKdwHseOrOM+A4B3hixkQzYqPKhgg6UZeL53+Ne//nXZkPGwgh1eAPniiy+WMFV99XhH1HpUmqE7b53Uq1vtIAc+ZX0KUts2c2wy/e1vf1v+M5fw1n1TGz3CYucztFX3EpRB03fUmHR+zDH9qou38TButfcYT+VMoBOk8aTPJnB8m2jwb8wf43/t1y8KTsqn2IyCsks7rgGorMFyPITmYHn9CuBqtwHGb22Q2nLT33O1juoB7O9+97sl7V8heJ7Wt3/sqno6RBnAerlZf7r/6OgTIdK+PetpIF7ZN239qzzlfTPWBpXbI61JyTz7yfjaEe14iA52laVn/P3WOt9V77FrjaVyeAesx+ptu04u9eNBP3iitdxzvLfxupW8i4JzraQJzhS/LnPoeeATThpYN/oBIgJIYdI0eOlma+l4qCPERfLcNrGuVF84DHAMw6N32uDhPfNqvQlo8vrZDOpB9trq48r4T8N2PaPMW58DRHisJ6Tanu3LO5XW8s4lxS7e//rXv971Xbn4NLnKI2v9kF6HvcrcIv3Hii/Uu2n4FJ6SGwTH6UGIoUzXd4lVvVmWodvxNIizbXzmgGuj68oGSuXiN+UASrytOz0w4AEDJO/169dLehokns3w0oFv8tR+bTVZrSeLhfGRf7TVDwtyaM/xHETm+DtGbg3ZGHuMrMl9jV4kEjU54ZdujFtjbZlgXW5ivHW6ODgvrUCGlmHbpLHZ4kt2BjbjSYZpQOVd+hgok5G8TQr7tM0o46H8OftAR2t+2gsU+8jXVyqUNVEhPB/rp+uPtZ8cTwXOJoSlU6s/5L80XTU43TaJGkjrPZ5zGnRl5nFtlPPaOdNACYwGOlAKfWeY/VB724wDP7/6+1Dd95XPSNuM0+abtzvm0tOARRG8XdGE649R9R0bL+n3HdZqe63z5HmsD6dcv2pw6rjBDojSAGu3NiAoQ5Ep05Fhz+vKXIK04RfIDgVU9cimrl8Gey55tbFtE24fWacs87aR/Bme07k2LB2EpbPervYBAq2BcQjAz6EnuiBDNoTn7MM52tjG46rB2Rf5dKwB8xQOzxRRIoBMxXbtfR55DZNIgOu4jwwMo/4pvw9w9uGLD7nWt6/oah/jUw4IK+s4n08OXGQxBvqg343FY+2rg9SJlzpTF0uBC/1Jzm3szzUG23iX9x8rLucKjwaOkVCYB9/7vmxd2aXkylziyFjJVBiWgWkrg36sXfWnIainr4eAe1cb+DB2stHToboqanHvdoa3NnZ28apP+7Q/5ZKu7q5+nePaHK9tk8s52tjF46rByTAocA4Wr/nnP//53exqMAOCcozmKWZeO5gZ8iHAmmXJP/u6a2CPvcYI09djPNpZVS6POfOqT+bAX95Dbazb3wXweF3qmOcmw0Nh+aXaxveqwdnA8SSR3VprzmZuRtGA200EEqFcdat3qaO228Wsjbk+K++hY4B2fdZbvzT+UP198qcuyOs383bxUDaic6BbAxSv9SQ6+c/0bB+vKcucmGad2j/3cU4gJvRDN7ROleeqwTm9yjSSHr8zgHNAlaHgWe9UBT5Wv/aBTLq2Ges+NA29ScgtI8/knkr00+R1DC/GW/+m/kvX12281d2n/QnCCZba2Mb7XHm72piynKu9NZ/3Bs5CyQxsLcgx5w0+JVKWn9sovpDHaAJABs7zVKf2gDVqbYhPA1Pdzqf8vYepfkaal5ztqxufOajJkgHWBiDjk/z4d82zv0gd74zWXl6186XQ5k/t5YEbh/V152QWvs12K3eLx8ZE36be0tVT9/mi4JyPq9VR/2skoyzvlOP8JCSD9Rzs3K3tcyVA1XuXPA8jfP32yR4hYgZpYJJPGeQY+JK1MsAdcBpUAKh8fNUL2JWXZ6e0eoyleq6VP9vwbqqH9vV19lP53pSx/tMGYNZ+bSZ37ciXxo/ceMwJC99bpe+++27pKx1M3T2X/l4UnHXSwGcUeZvOK3PMMYNjgBkb79e7mz6RyYA9lB5oedYPP/zw3Stbno2t/AcffLA84N5D8N4a8UI1Pp6TtZ7Fb6bJzWsFFIDoP4e5Jn/dV7ICgmd3o4DYeXUmUPRzzvZkd71JRN30EJ88pzGYNMtVxpEHWcsy691SusmyPqWTqeOuPcXxouBkEA08wwpM5+xoYVqKxdvXBhi39yz7twtA5gVoH9V68eLFIoJPYAoN/3fzMraXsj2s3qcpfQHPC9DeKPFJTCDz8Lt/x+e1L48IAm/53jrxdJLzwO7LBp4bNSH41/NersbThpVy8v74xz8uafx8GtN9Wnw9cM9DetG7f8Y09ae+SWMSHfOa33///X+BWBnXHqI1cB8qd4v52ed6WTB1/VT9vig4ddzAT8Pw4WR0DoPAN+UySoDEd878tT090D7KbvaMv49o4eXdzx9//HFhASC+cPCPzYPY/o38N998s7Qtrex8IMJ7oMr7CgIPjHw5/ve///2S9joZgDKSP/3pT8ura9oGdH1q8umokv9c5v6i/tZPE019rawjY8sb45fxaUP6HOOxdOSK/qSD+dJDuptr0Kfq0kXBWacYQIOfsaeYypxybNarDUbIYLv3hneApfyMVvnCbGXKB0zyCReTs/rKyd/msV3TNhDiXV+TSz4CRDL7r9eoNoBZnT6v6drPP//ssFAArF95bhe1m0z4+XX+79r/aYc8tela45PMgbl6t3xsramPjfHMe8q+XxScjDgDdfzll1+WvmZcp3Y874ZPiu3LBAGtozIZt/Q0Tud5FelZx3mUsXdkzGZYR+uXZChPPV4VxR8om53VQ/NLDXMdtNaT8m2AkdGL4Na39UX7s05tLo1s/sxr5W07aqdx23b9lvJ6q6b/ukavD43/++73RcFZZxhzHc6wO6/MKceMvSNe+Ge0HdehivwAIj2vAwlZp5FKB554AkBlgN+EUd8CK3maGNbH9FFdZVH50vrVufdJeWDrVp4TreWUR67a0i/A/Omnn/5Lvin7rwmQ9DNJxEJH3aZybU78s+z7TJ8Ezml8hO78OXTsfSrxUm3NyUIbgR44fX3huVMTmMmliYLMh9hHfTaR4Ofcpl28T9EBHnjhKa0NVJun8D5H3ZPAmQAU/1w6lEy3cuSVgTTD0S+f9rgWsrThle06ozdv3izHGeUsGVv+AMw2EP7www9bSh+XtY3XQ+0e18Lxtc4CTjNhStzW2ePF+3XX3DbpZdRrr/ocNZVN6EdPX5Gz/MdkbrnQ0mM6gPIe47Hr+uQR7/Jqe1f9S187CZzN5jpSZ169evUufWnhb51/ywT9ZOB+yKZSxrRkPNM/gTDbIKb0IWFtXVMPv+qeY0c1HjmXKWftPuXxJHA+peD3tu8auHUN3MF56yN879/VauAOzqsdurvgt66BOzhvfYTv/btaDdzBebVDdxf81jVwB+etj/C9f1ergTs4r3bo7oLfugbu4Lz1Eb7372o1cAfn1Q7dXfBb18AdnLc+wvf+Xa0G7uC82qG7C37rGriD89ZH+N6/q9XAHZxXO3R3wW9dA3dw3voI3/t3tRq4g/Nqh+4u+K1r4A7OWx/he/+uVgN3cF7t0N0Fv3UN3MF56yN879/VauD/ABia8ZC78qcLAAAAAElFTkSuQmCC" alt="" />
Question 35 :
A force acting against achievement of highest possible level of population growth is
Question 36 :
Which of the following is not a function of auxin ?
Question 37 :
Read the following statements<br>A) Cerebellum has very convoluted surface to provide additional space for more neurons<br>B) Two olfactory lobes and two optic lobes collectively termed as corpora quadrigemina<br>C)Amygdala, hippocampus are the inner deeper parts of cerebral hemispheres<br>D) Corpus callosum connects the two halves of cerebellar hemispheres<br>Among them, the correct combinations are
Question 39 :
Choose any one of the following four responses.
A. If Assertion is True but the Reason is False.
B. If both Assertion & Reason are False.
C. If both Assertion & Reason are True & the
Reason is a correct explanation of the Assertion.
D. If both Assertion & Reason are True but Reason
is not a correct explanation of the Assertion.
<br>Assertion-Phototopic vision is also called twilight vision.
Reason :-Person can differentiate colour in day light.
Question 40 :
Assertion :- C2 molecule contains 2{tex}\pi{/tex}bonds.
Reason :- C2 is paramagnetic at room temperature
Question 42 :
Due to efforts of Mr. Ramdeo Misra, the government of India established the.....(1972) which in later years, paved the way for the establishment of the Ministry of environment and forests (1984) :-
Question 43 :
What will happen to a well growing herbaceous plant in the forest if it is transplanted outside the forest in a park ?
Question 45 :
The study of fossils in different aged rock showed that most fossils exist in :-