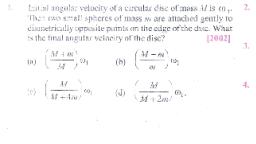Question 1 :
The sum <sup>40</sup>C<sub>0</sub> + <sup>40</sup>C<sub>1</sub> + <sup>40</sup>C<sub>2</sub> + … + <sup>40</sup>C<sub>20</sub> is equal to
Question 3 :
If the sum of the coefficient in the expansion of (a<sup>2</sup>x<sup>2</sup> − 6ax + 11)<sup>10</sup>, where a is constant is 1024, then the value of a is
Question 4 :
The term independent of x in the expansion of $\left( \sqrt{\frac{x}{3}} + \frac{3}{{2x}^{2}} \right)^{10}$ will be
Question 5 :
$\ ^{47}C_{4} + \sum_{r = 1}^{5}\text{\ \ }\ ^{52 - r}C_{3}$ is equal to
Question 6 :
An infinite GP has first term x and sum 5, then
Question 7 :
If |x| < 1, then the coefficient of x<sup>3</sup> in the expansion of log (1 + x + x<sup>2</sup>) is ascending powers of x, is
Question 8 :
If $S = \sum_{n = 1}^{\infty}{\left( \frac{\ ^{n}C_{0} + \ ^{n}C_{1} + \ ^{n}C_{2} + \ldots + \ ^{n}C_{n}}{\ ^{n}P_{n}} \right),}$ then S equals
Question 9 :
An infinite GP has first term x and sum 5, then x belongs to
Question 10 :
In a GP the sum of three numbers is 14, if 1 is added to first two numbers and subtracted from third number the series becomes AP, then the greatest number is
Question 11 :
If $\log _{ 3 }{ \left( x-1 \right) <\log _{ 0.09 }{ \left( x-1 \right) } }$ then $x$ lies in the interval:
Question 12 :
Let $\displaystyle \alpha =\frac{\pi}{3},$ then the solution set of the inequality $\displaystyle \log _{\sin \alpha }(2-\cos ^{2}x)<\log _{\sin \alpha }(1-\sin x),$ where $\displaystyle x \varepsilon (0.2\pi )$ and $\displaystyle x\neq \frac{\pi }{2}, $ is :
Question 13 :
Solve the inequation: $\log _{\sqrt{2}} (5^{x}- 1).\log _{\sqrt{2}} \left ( \cfrac{2\sqrt{2}}{5^{x}-1} \right ) > 2.$<br/>
Question 14 :
<font>The no. of ways in which 30 marks can be signed to 8 questions giving not less than 2 marks to any questions.</font></p>
Question 15 :
<font>If the number of ways of selecting K cards out of unlimited number of cards bearing the number 0, 9, 3 so that they can’t be used to write the number 903 is 93, then K is equal to</font></p>
Question 16 :
<font>The no. of ways 360 can be resolved into product of two positive integral factors is</font></p>
Question 17 :
A binary sequence is an array of 0’s and 1’s. The number of n−digit binary sequence which contain even number of 0’s is
Question 18 :
The value of $\ ^{35}C_{8} + \sum_{r = 1}^{7}{\ ^{42 - r}C_{7}} + \sum_{s = 1}^{5}{\ ^{47 - s}C_{40 - s}}$ , is
Question 19 :
<font>The no. of ways can 5 balls be distributed into 3 boxes so that every box contains at least one ball if balls are different and boxes are different</font></p>
Question 20 :
If N is the number of positive integral solution of x<sub>1</sub>x<sub>2</sub>x<sub>3</sub>x<sub>4</sub> = 770, then the value of N is
Question 21 :
If 0 ≤ x ≤ π and 81<sup>sin<sup>2</sup>x</sup> + 81<sup>cos<sup>2</sup>x</sup> = 30, then x is equal to
Question 22 :
In a triangle ABC, if a = 2, B − 60<sup>∘</sup> and C = 75<sup>∘</sup>, then b=
Question 24 :
The value of the expression 3(sinx−cosx)<sup>4</sup> + 4(sin<sup>6</sup>x+cos<sup>6</sup>x) + 6(sinx+cosx)<sup>2</sup> is
Question 25 :
If$\ x\cos{\theta = y\cos{\left( \theta + \frac{2\pi}{3} \right) = \mathcal{z}\cos\left( \theta + \frac{4\pi}{3} \right)\ }}$, then the value of $\frac{1}{x} + \frac{1}{y} + \frac{1}{\mathcal{z}}$ is equal to