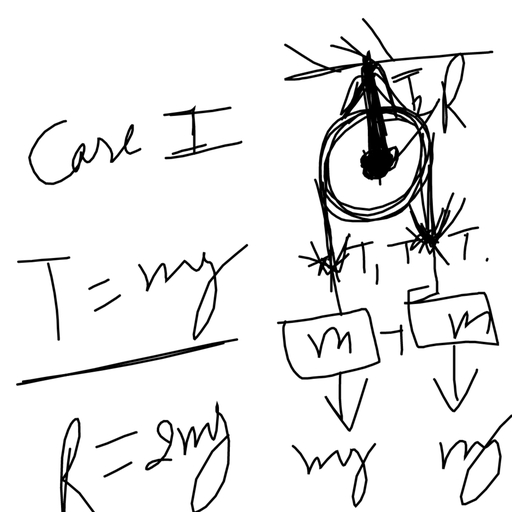
Question 1 :
Distance travelled by a particle at any instant {tex}\mathrm{'t'}{/tex} can be represented as {tex}\mathrm{ S = A ( t + B ) + C t ^ { 2 }} . {/tex} The dimensions of {tex}\mathrm{B}{/tex} are
Question 2 :
If {tex}\mathrm L = 2.331 \mathrm { cm } ,\mathrm B = 2.1 \mathrm { cm } , {/tex} then {tex} \mathrm { L } + \mathrm { B } = {/tex}
Question 4 :
Which one of the following represents the correct dimensions of the gravitational constant?
Question 5 :
Young's modulus of steel is {tex} 1.9 \times 10 ^ { \mathrm { 11 } } \mathrm { N } / \mathrm { m } ^ { 2 } {/tex} When expressed in CGS units of dyne/cm {tex} ^ { 2 } {/tex}, it will be equal to {tex} \left( 1 \mathrm { N } = 10 ^ { 5 } \mathrm { dyne } , 1 \mathrm { m } ^ { 2 } = 10 ^ { 4 } \mathrm { cm } ^ { 2 } \right) {/tex}
Question 6 :
Error in the measurement of radius of a sphere is {tex} 1 \% . {/tex} Then error in the measurement of volume is
Question 9 :
The quantity having the same units in all systems of units is
Question 10 :
The division of energy by time is {tex} \mathrm { X } . {/tex} The dimensional formula of {tex} \mathrm { X } {/tex} is same as that of
Question 11 :
Which one of the following represents the correct dimensions of the coefficient of viscosity?
Question 12 :
The heat generated in a circuit is given by {tex} Q = I ^ { 2 }Rt {/tex} , where {tex} \mathrm I {/tex} is current, {tex} R {/tex} is resistance and {tex} \mathrm t {/tex} is time. If the percentage errors in measuring {tex}I, R {/tex} and t are {tex} 2 \% , 1 \% {/tex} and {tex} 1 \% {/tex} respectively, then the maximum error in measuring heat will be
Question 15 :
{tex} \left[ \mathrm { MLT } ^ { - 1 } \right] + \left[ \mathrm { MLT } ^ { - 1 } \right] = \ldots \ldots \ldots \ldots {/tex}
Question 16 :
What are the dimensions of {tex} \mathrm { A } / \mathrm { B } {/tex} in the relation {tex} \mathrm { F } = \mathrm { A } \sqrt { \mathrm { x } } + \mathrm { Bt } ^ { 2 } , {/tex} where {tex}\mathrm F {/tex} is the force, {tex} x {/tex} is the distance and {tex} t {/tex} is time?
Question 18 :
In a simple pendulum experiment, the maximum percentage error in the measurement of length is {tex} 2 \% {/tex} and that in the observation of the time- period is {tex} 3 \% . {/tex} Then the maximum percentage error in determination of the acceleration due to gravity g is
Question 19 :
If {tex} x = a t + b t ^ { 2 } , {/tex} where {tex} x {/tex} is the distance travelled by the body in kilometers while {tex} t {/tex} is the time in seconds, then the unit of {tex} b {/tex} is
Question 22 :
Which of the following physical quantities has neither dimensions nor unit?
Question 23 :
The resistance {tex} R {/tex} of a wire is given by the relation {tex} R = \frac { \rho \ell } { \pi r ^ { 2 } } . {/tex} Percentage error in the measurement of {tex} \rho , \ell {/tex} and {tex} r {/tex} is {tex} 1 \% , 2 \% {/tex} and {tex} 3 \% {/tex} respectively. Then the percentage error in the measurement of {tex} R {/tex} is
Question 24 :
{tex} \mathrm { E } , \mathrm { m } , \mathrm { J } {/tex} and {tex} \mathrm { G } {/tex} denote energy, mass, angular momentum and gravitational constant respectively, then the unit of {tex} \frac { \mathrm { E } \mathrm { J } ^ { 2 } } { \mathrm { m } ^ { 5 } \mathrm { G } ^ { 2 } } {/tex} is
Question 26 :
A force is given by {tex} \mathrm { F } = \mathrm { at } + \mathrm { bt } ^ { 2 } , {/tex} where t is time, the dimensions of a and b are
Question 27 :
Which one of the following is not measured in units of energy?
Question 28 :
In a simple pendulum experiment, the maximum percentage error in the measurement of length is {tex} 2 \% {/tex} and that in the observation of the time-period is {tex} 3 \% . {/tex} Then the maximum percentage error in determination of the acceleration due to gravity {tex} \mathrm { g } {/tex} is
Question 29 :
You measure two quantities as {tex} A = 1.0 \mathrm { m } \pm 0.2 \mathrm { m } {/tex} {tex},B = 2.0 \mathrm { m } \pm 0.2 \mathrm { m } . {/tex} We should report correct value for {tex} \sqrt { A R } {/tex} as
Question 30 :
Which one of the following is not a unit of Young’s modulus?
Question 31 :
Write the dimensions of a {tex} \times b {/tex} in the relation {tex} E = \frac { b - x ^ { 2 } } { a t } , {/tex} where {tex} E {/tex} is the energy, {tex} x {/tex} is the displacement and {tex} t {/tex} is time
Question 32 :
The unit of permittivity of free space, {tex} \varepsilon _ { \mathrm { o } } {/tex} is
Question 33 :
Resistance {tex} \mathrm { R } = \mathrm { V } / \mathrm { I } , {/tex} here {tex} \mathrm { V } = ( 100 \pm 5 ) \mathrm { V } {/tex} and {tex} \mathrm { I } = ( 10 \pm 0.2 ) \mathrm { A } . {/tex} Find percentage error in {tex} \mathrm { R } . {/tex}
Question 34 :
If {tex} \mathrm { v } = \frac { \mathrm { a } } { \mathrm { t } } + \mathrm { bt } ^ { 3 } {/tex} where {tex} \mathrm { v } = {/tex} velocity and {tex} \mathrm { t } {/tex} is time The dimensional formula of {tex} \mathrm { a } {/tex} and {tex} \mathrm { b} {/tex} are
Question 35 :
In a vernier callipers, ten smallest divisions of the vernier scale are equal to nine smallest division on the main scale. If the smallest division on the main scale is half millimeter, then the vernier constant is
Question 36 :
If the dimensions of a physical quantity are given by {tex} \mathrm { M } ^ { \mathrm { a } } \mathrm { L } ^ { \mathrm { b } } \mathrm { T } ^ { \mathrm { c } } , {/tex} then the physical quantity will be
Question 37 :
The refractive index of water measured by the relation {tex} \mu = \frac { \text { real depth } } { \text { apparent depth } } {/tex} is found to have values of {tex} 1.34,1.38,1.32 {/tex} and {tex} 1.36 ; {/tex} the mean value of refractive index with percentage error is
Question 38 :
If force (F), length (L) and time (T) assumed to be fundamental units, then the dimensional formula of the mass will be
Question 39 :
Match the columns I and II<br>{tex} \begin{array} { l l } { }{ \text { Column } \mathrm { I } } & { \text { Column } \mathrm { II } } \\ { \text { (A) Practical unit } } & { \text { (1) } \text { radian } } \\ { \text { (B) Base unit } } & { \text { (2) light year } } \\ { \text { (C) Derived unit } } & { \text { (3) } \mathrm { kg } - \mathrm { ms } ^ { - 1 } } \\ { \text { (D) Complementary unit } } & { \text { (4) second } } \end{array} {/tex}<br>
Question 40 :
An experiment is performed to obtain the value of acceleration due to gravity g by using a simple pendulum of length L. In this experiment time for 100 oscillations is measured by using a watch of 1 second least count and the value is 90.0 seconds. The length L is measured by using a meter scale of least count 1 mm and the value is 20.0 cm The error in the determination of g would be:
Question 41 :
Surface tension of a liquid is {tex} 70 \mathrm {\ dyne } / \mathrm { cm } {/tex}. Its value in SI is
Question 42 :
In order to measure physical quantities in the sub-atomic world, the quantum theory often employs energy [E], angular momentum [J] and velocity [ c] as fundamental dimensions instead of the usual mass, length and time. Then, the dimension of pressure in this theory is
Question 43 :
The displacement of a body at a particular second {tex} \mathrm { n } {/tex} is given by the expression {tex} \mathrm { S } _ { \mathrm { nth } } = \mathrm { u } + \frac { \mathrm { a } } { 2 } ( 2 \mathrm { n } - 1 ) . {/tex} The dimensional formula of {tex} \mathrm { S } _ { \mathrm { nth } } {/tex} in this equation is
Question 44 :
The frequency (f) of a wire oscillating with a length {tex} \ell , {/tex} in {tex} \mathrm { p } {/tex} loops, under a tension {tex} \mathrm T {/tex} is given by {tex} \mathrm { f } = \frac { \mathrm { p } } { 2 \ell } \sqrt { \frac { \mathrm { T } } { \mu } } {/tex} where {tex} \mu = {/tex} linear density of the wire. If the error made in determing length, tension and linear density be {tex} 1 \% , - 2 \% {/tex} and {tex} 4 \% , {/tex}, then find the percentage error in the calculated frequency.