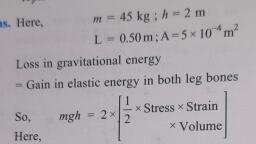Question 2 :
Check whether the following is a quadratic equation.$(x - 3) (2x + 1) = x (x + 5)$<br/>
Question 4 :
If c is small in comparision with l then ${\left( {\frac{l}{{l + c}}} \right)^{\frac{1}{2}}} + {\left( {\frac{l}{{l - c}}} \right)^{\frac{1}{2}}} = $
Question 5 :
The roots of the equation $\sqrt{3y + 1} = \sqrt{y - 1}$  are?<br/>
Question 6 :
When $a = \dfrac {4}{3}$, the value of $27a^{3} - 108a^{2} + 144a - 317$ is
Question 7 :
For what values of $k$, the equation $x^{2}+2(k-4)x+2k=0$ has equal roots?
Question 8 :
Is the following equation a quadratic equation?$\displaystyle 3x + \frac{1}{x} - 8 = 0$
Question 9 :
Let x and y be two 2- digit number such that y is obtain by reversing the digits of x.suppose they also satisfy $x^2-y^2=m^2$ for some positive integer m. The value of $x+y+m$ is.
Question 10 :
Is the following equation a quadratic equation?$\displaystyle \frac{3x}{4} - \frac{5x^2}{8} = \frac{7}{8}$
Question 11 :
The roots of the equation $(b+c)x^2-(a+b+c)x+a=0$ $(a,b,c\ \epsilon \Q, b+c \neq a)$ are
Question 12 :
Find the values of $k$ for the following quadratic equation, so that they have two real and equal roots:$4x^2 - 2(k + 1)x + (k + 4) = 0$
Question 13 :
if x be real and 0 < b< c then $ \dfrac { { x }^{ 2 }-bc }{ 2x-b-c } $<br/><br/>
Question 14 :
For the equations $x^2+ bx + c = 0$ and $2x^2+ (b + 1)x + c + 1 = 0$ select the correct alternative
Question 16 :
Each of the equations $3x^2 - 2 = 25, (2x - 1)^2 = (x - 1)^2, \sqrt{x^2 - 7} = \sqrt{x - 1}$ has
Question 17 :
If $x_1$ and $x_2$ are the roots of $3x^2 - 2x - 6 = 0$, then $x_1^2 + x_2^2$ is equal to
Question 18 :
If $\alpha $ and $\beta$ are roots of $x^{2}$ - $(k + 1)$ $x$ + $\dfrac{1}{2}$ $(k^{2}+k+1)$ $=$ 0, then $\alpha ^{2}+\beta ^{2}$ is equal
Question 19 :
If $\alpha$, $\beta$  are the roots of $3x^{2} - 4x + 1 = 0$ the equation whose roots are $\dfrac{\alpha}{\beta}, \dfrac{\beta}{\alpha}$ is?<br/>
Question 20 :
If both a and b belong to the set $\displaystyle \left\{ 1,2,3,4 \right\}$ then the number of equations of the form $ ax^{2}+bx+1=0$ having real roots is :<br>
Question 21 :
If one of the roots of $\displaystyle x^{2}+f(a)x+a=0$ is equal to third power of the other for all real $a$, then 
Question 22 :
Let $a,b,c$ be real and $ { ax }^{ 2 }+bx+c=0$ has two real roots, $\alpha$ and $\beta$ where $\alpha <-1$ and $\beta > 1$, then $ 1+\dfrac { c }{ a } +\left| \dfrac { b }{ a } \right| < 0$ is
Question 23 :
If both the roots of the equation ${ x }^{ 2 }-32x+c=0$ are prime numbers then the possible values of $c$ are
Question 24 :
If $m_1$ and $m_2$ are the roots of the equation $x^2+\left(\sqrt{3}+2\right)x+\left(\sqrt{3}-1\right)=0$, then the area of the triangle formed by the lines $y=m_1x,y=m_2x$ and $y=2$ is :
Question 25 :
The coefficient of $x$ in the equation $x^2+px+q=0$ was wrongly written as $17$ in place of$13$ and the roots thus found was $-2$ and $-15$.<br>Then the roots of the correct equation are