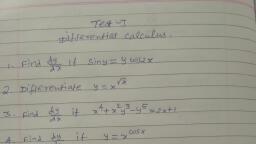Question 1 :
f : R → R be a differentiate function " x ∈ R. If tangent drawn to the curve at any point x e (a, b) always lie below the curve then
Question 2 :
The value of 'a' for which the equation x<sup>3</sup> - 3x + a = 0 has two different roots in [0, 1] is given by -
Question 3 :
L'' (x) > 0 " x ∈ R and g(x) = f(2 - x) + f(4 + x). Then g(x) is increasing in -
Question 4 :
The function f(x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74bfc3f511820358e68f92' height='37' width='88' >is increasing for x ∈ R when
Question 6 :
If e<sup>x</sup> +xy = e, then dy/dx at x = 0 is -
Question 7 :
If "x & y, f(x + y) = f(x)⋅f(y) and f(5) = 2, f ′(0) = 3 then f ′(5) equals
Question 8 :
Let f & g are differentiable function which satisfies g ′(m) = 4 & g(m) = b and fog(x) is an identity function then f ′(b) is <br>equal to
Question 9 :
The normal to the curve x = a(1 + cos θ), y = a sin θ at 'θ' point always passes through the fixed point -
Question 10 :
If y = 4x - 5 is tangent to the curve y<sup>2</sup> = px<sup>3</sup> + q at (2, 3), then
Question 11 :
If for a continuous function f, f(0) = f(1) = 0 & f '(1) = 2 and g(x) = f(e<sup>x</sup>). e<sup>f(x)</sup> then g'(0) is equal to -
Question 12 :
The value of a for which the function f(x) = sin x - cosx -ax + b decreases for all real values of x is given by
Question 13 :
The tangent to the curve y = e<sup>2x</sup> at the point (0, 1) meets the x- axis at
Question 14 :
In (-4, 4) the function f(x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c03cf511820358e69038' height='49' width='56' >e<sup>-4t</sup> dt has -
Question 15 :
f(x) satisfies the conditions of Rolle's theorem in [1, 2] and f(x) is continuous in [1, 2] then <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74bf6df511820358e68f36' height='49' width='41' >dx is equal to -
Question 16 :
If for a function f, |f(x) - f(y)| ≤ (x - y)<sup>2</sup> " x, y ∈ R, then f is -
Question 17 :
f(x) = x<sup>9</sup> + 3x<sup>7</sup> + 64 is monotonic increasing for -
Question 18 :
Let f(x) = Max. {x +1, |x| +1}. Then f(x) is non differentiable at
Question 19 :
Let f : R → R be a continuous onto function satisfying f(x) + f(-x) = 0, " x ∈ R. If f(-3) = 2 and f(5) = 4 in [-5, 5], then the equation f(x) = 0 has
Question 20 :
In the interval (1, 2), function f(x) = 2|x - 1| + 3| x - 2| is
Question 21 :
f(x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c030f511820358e6902a' height='55' width='91' > then at x = 0, function is -
Question 22 :
Let f : [a, b] → R be a function such that for c∈(a, b), f ′(c) = f ″(c) = f ″′(c) =f <sup>iv </sup>(c) = f <sup>v</sup>(c) = 0, then :
Question 23 :
Let f(x) = sin x; g(x) = x<sup>2</sup> and h(x) = log x. <br>If u (x) = h (f (g (x))), then <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74be2b46f7eb01d9e6e67a' height='40' width='28' > is
Question 24 :
The value of the function f(x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c02df511820358e69026' height='49' width='176' > is minimum at -
Question 25 :
If x cos y + y cos x = π, then y " (0) =
Question 26 :
If the trinomial x<sup>2</sup> + px + q has a minimum at x = 3 and minimum value is equal to 5, then p and q are -
Question 27 :
Let ƒ(x) satisfy the requirements of Lagrange's mean value theorem in [0, 2]. If ƒ(0) = 0 and ƒ′(x) ≤<img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74bd2bf511820358e68c67' height='36' width='15' > for all x in [0, 2], then -
Question 28 :
f(x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c046f511820358e69045' height='41' width='75' >then for f(x), x = 1 is -
Question 29 :
The function f(x) = x(x<sup>2 </sup>- 4)<sup>n</sup>(x<sup>2 </sup>- x +1), n ∈ N assumes a local minima at x = 2 then
Question 30 :
The product of the lengths of sub tangent and subnormal at any point of a curve is equal to
Question 31 :
The surface area of a sphere when its volume is increasing at the same rate as its radius is-
Question 32 :
Let ƒ(x) = x<sup>3</sup>/4 - sin πx + 3. If ƒ(x) takes the value α on [-2, 2] then α is equal to -
Question 33 :
Let f and g be differentiable function such that f′(x) = 2g(x) and g′(x) = -f(x), and let T(x) = (f(x))<sup>2</sup> - (g (x))<sup>2</sup>.<br>Then T′(x) is equal to
Question 34 :
Number of critical points of f (x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c065d374484379aa89d3' height='39' width='51' > is
Question 35 :
The function f(x) = 1+x(sin x) [cos x], 0 < x ≤π/2 & [.] = G.I.F
Question 36 :
The function f(x) = 1 + x sin x[cos x], 0 < x ≤/2, [⋅] = G.I.F.
Question 37 :
Segment of the tangent to the curve xy = c<sup>2</sup> at the point (x′, y′) which is contained between the coordinate axes, is bisected at the point -
Question 38 :
If f(x) = x<sup>3</sup> + bx<sup>2</sup> + cx + d, 0 < b<sup>2</sup>< c, then f(x) is -
Question 39 :
If f(x) = |x - 25| and g(x) = f(f(x)) then for x > 50, g′(x) is equal to -
Question 40 :
If f(x) = cos <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74beeff511820358e68e9c' height='41' width='71' >, 1 < x < 2 where [.] is the greatest integer then f ′(<img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74beef46f7eb01d9e6e761' height='23' width='37' >) is
Question 41 :
Let x ∈<img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74bfab023ac44295581bd5' height='41' width='41' >, f(x) = x tan(sin x), g(x) = xsin(tanx) and h(x) = sinx tanx. Which one is greatest ?
Question 42 :
The tangent to the curve y = 2x<sup>2</sup> - x + 1 is parallel to the line y = 3x + 9 at the point whose co-ordinates are :
Question 43 :
Let f : R → R be a function satisfying f(x + y) = f(x) + λxy + 3x<sup>2</sup>y<sup>2</sup> for all x, y ∈ R. If f(3) = 4 and f(5) = 52 then f ' (x) is equal to -
Question 44 :
Let ƒ(x) be a polynomial function of second degree. If f(1) = f(-1) and a, b, c are in A.P., then ƒ′ (a), ƒ′ (b), ƒ′ (c) are in -
Question 45 :
The number of critical points of f (x) = max (sin x, cos x) for x ∈ (0, 2π)
Question 46 :
Equation of normal to the curve y = x + sin x cos x at x = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74bd2f2ca8b87fce151f6a' height='36' width='15' >is
Question 48 :
Let f(x) =<img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74bfdaf511820358e68fb4' height='39' width='65' >, x ∈ (-∞, ∞) then the interval for which f(x) is increasing is -
Question 49 :
Let f(x) = x<sup>3</sup> + bx<sup>2</sup> + cx +d ; 0 < b<sup>2</sup>< c then f(x) :
Question 50 :
The function f(x) = cot<sup>-1</sup>x + x increases in the interval :
Question 51 :
The equation x<sup>3</sup> - 3x + a = 0 will have exactly one real root if
Question 52 :
If ƒ(x) = x(x - 2) (x - 4), 1 ≤ x ≤ 4, then a number satisfying the condition of the mean value theorem is -
Question 54 :
The ends A and B of a rod of length <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74bef5f511820358e68ea3' height='23' width='21' > are sliding along the curve y = 2x<sup>2</sup>. Let x<sub>A</sub> and x<sub>B</sub> be the x-coordinate of the ends. At the moment when A is at (0, 0) and B is at (1, 2) the derivative <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74bef546f7eb01d9e6e769' height='40' width='31' > has the value equal to -
Question 55 :
The equation of the tangent to the curve f (x) = 1 + e<sup>-2x</sup> where it cuts the line y = 2 is
Question 56 :
Locus of a point at which the circles x<sup>2</sup> + y<sup>2</sup> -2x -2y -7 = 0 and x<sup>2</sup> + y<sup>2</sup> + 8x + 6y = 0 subtend equal angles, is -
Question 57 :
Given a function f : [0, 4] ―→ R is differentiable, then for some a, b ∈ (0, 4) [f(4)]<sup>2</sup> - [f(0)]<sup>2</sup> =
Question 58 :
If the function f(x) = 2 tan x + (2a +1) log<sub>e</sub> |secx | + (a -2) x is increasing on R, then-
Question 59 :
Let f(x) be a polynomial function of second degree. If f(1)= f(-1) and a,b,c are in A.P, then f' (a), f' (b), f' (c) are in [2003]
Question 60 :
Let f(x) = ax<sup>3</sup> + bx<sup>2</sup> + ex + d, a ≠ 0. If x<sub>1</sub> and x<sub>2 </sub>are the real and distinct roots of f '(x) = 0 then f(x) = 0 will have three real and distinct roots if
Question 61 :
If y = a ln | x + 1 | + b (x + 1)<sup>2 </sup>+ x has its extremum value 4 at x = 0, then (a, b) is -
Question 62 :
If M be the greatest value and m be the least value of ƒ(x) = 2x<sup>3</sup> - 3x<sup>2</sup> - 12x + 1, for -1 ≤ x ≤ 3/2, then the ordered pair (M, m) is -
Question 63 :
If y = f(x) is differentiable at x = a and y = g(x) is continuous but not differentiable at x = a, g'(a<sup>+</sup>) & g'(a<sup>-</sup>) are finite, the which one of the following is INCORRECT ?
Question 64 :
The maximum area of the rectangle whose sides pass through the angular points of a given the rectangle is of sides a and b is
Question 65 :
If y = (1 + x) (1 + x<sup>2</sup>) (1 + x<sup>4</sup>) .... (1 + x<sup>2n</sup>) then <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74bd1a46f7eb01d9e6e522' height='37' width='21' > at x = 0 is
Question 67 :
The function f(x) = sin<sup>4 </sup>x + cos <sup>4</sup> x increasing if -
Question 68 :
Given f(x) = 4 -<img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c08cf511820358e690a7' height='43' width='63' >; g(x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c08c023ac44295581d05' height='55' width='96' >; h(x) = {x}, k (x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c08dd374484379aa8a09' height='20' width='52' >, Then in [0, 1] Langranges Mean value theorem is NOT applicable to:
Question 69 :
If the function f(x) = |x<sup>2</sup>+ a |x| + b| has exactly three points of non-differentiability, then which of the following may hold
Question 70 :
A function ' f ' is such that f'(a) = f''(a) = f'''(a) = ... f<sup>(2n)</sup> (a) = 0, and ' f ' has a local maximum value ' b' at x = a, if f (x) is equal to -<sup>
Question 71 :
The acute angles between the curves y = |x<sup>2</sup> - 1| and <br>y = |x<sup>2</sup> - 3| at their points of intersection is -
Question 72 :
Let f(x) = x<sup>3</sup> + 6x<sup>2</sup> + px + 2. If the largest possible interval, in which f(x) is a decreasing function, is (-3, -1), then p equals
Question 73 :
Suppose the cubic {tex} x ^ { 3 } - p x + q {/tex} has three distinct real roots where {tex} p > 0 {/tex} and {tex} q > 0 . {/tex} Then which one of the following holds?
Question 74 :
The largest value of 2x<sup>3</sup> - 3x<sup>2</sup> - 12x + 10 for - 2 ≤ x ≤4 occurs at x =
Question 75 :
If ƒ(x) = x ⋅ e<sup>x(1 - x)</sup>, then ƒ(x) is -
Question 76 :
Let f(x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74be3cf511820358e68dcf' height='47' width='151' >f(x) will be differentiable at x = 1, if
Question 77 :
Let g : R → R be a differentiable function satisfying g(x) = g(y) g(x - y) " x, y ∈ R and g' (0) = a and g' (3) = b then g' (- 3) is -
Question 78 :
The point of intersection of the tangents drawn to the curve x<sup>2</sup>y = 1 - y at the points where it is met by the curve <br>xy = 1 - y, is given by -
Question 79 :
Let f(x) = 2<sup>2x-1</sup> and φ(x) = -2<sup>x</sup> + 2x log 2. If f´(x) >φ′(x), then
Question 80 :
If the parabola y = f(x), having axis parallel to y-axis, touches the line y = x at (1, 1) then
Question 81 :
If {tex} f {/tex} is a real-valued differentiable function satisfying {tex} | f ( x ) - f ( y ) | \leq ( x - y ) ^ { 2 } , x , y \in R {/tex} and {tex} f ( 0 ) = 0 {/tex} then {tex} f ( 1 ) {/tex} equals
Question 82 :
If tangent at any point of the curve y = x<sup>3</sup> + λx<sup>2</sup> + x + 5 makes acute angle with x-axis, then -
Question 83 :
The function <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c014023ac44295581c63' height='40' width='60' > has no maximum or minimum if (k an integer) -
Question 84 :
If f(x) = log<sub>x</sub> (lnx) then f ′(x) at x = e is
Question 85 :
Let f(x), g(x) be two continuously differentiable functions satisfying the relationships f′(x) = g(x) and f′′(x) = - f(x). Let h(x) = [f(x)]<sup>2</sup> + [g(x)]<sup>2</sup>. If h(0) = 5, then h(10) =
Question 86 :
The coordinates of the point on the parabola y<sup>2</sup> = 8x, which is at minimum distance from the circle x<sup>2</sup> + (y + 6)<sup>2</sup> = 1 are-
Question 87 :
Two racers start a race at the same moment and finish in a tie. Which of the following must be true?
Question 88 :
The function f(x) =<img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74bd47f511820358e68c8e' height='47' width='180' > has a local max. at x =
Question 89 :
The greatest of the numbers 1, 2<sup>1/2</sup>, 3<sup>1/3</sup>, 4<sup>1/4</sup>, 5<sup>1/5</sup>, 6<sup>1/6</sup> and 7<sup>1/7</sup> is
Question 90 :
The function y = f(x) is represented parametrically by x = t<sup>5</sup> - 5t<sup>3</sup> - 20t + 7 and y = 4t<sup>3</sup> - 3t<sup>2</sup> - 18t + 3, (-2 < t < 2). The minimum of y = f(x) occurs at
Question 91 :
y = f(x) is a parabola, having it's axis parallel to y-axis. If the line y = x touches this parabola at x = 1, then
Question 92 :
Let f(x) be a polynomial function of second degree. If f(1) = f (-1) and a<sub>1</sub>, a<sub>2</sub>, a<sub>3</sub> are in AP then f '(a<sub>1</sub>), f '(a<sub>2</sub>), f '(a<sub>3</sub>) are in
Question 93 :
The function y = f(x) is defined by x = 2t - |t|, y = t<sup>2</sup> + t |t|, t ∈ R in the interval x ∈ [- 1, 1] then
Question 94 :
f(x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c033023ac44295581c8e' height='49' width='56' > (t - 1)(t - 2)<sup>3</sup>(t - 3)<sup>5</sup> dt has a local minimum at x equals :
Question 95 :
If 2x<sup>3</sup> -3x<sup>2</sup>y<sup>2</sup> + 4x - y + 7 = 0 and y(1) = 1, then the value of y′′(1) is equal to-
Question 96 :
The function f(x) = (4sin<sup>2</sup> x - 1)<sup>n</sup> (x<sup>2</sup> - x + 1), n ∈ N, has a local minimum at x = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74be75f511820358e68e13' height='37' width='15' >, then -
Question 97 :
The value of 'a' for which x<sup>3</sup> - 3x + a = 0 would have two distinct roots in (0, 1) is -
Question 98 :
If the function f(x) = <img style='object-fit:contain' src='https://storage.googleapis.com/teachmint/question_assets/JEE%20Main/5e74c0b8f511820358e690dc' height='39' width='64' >, where t is a parameter that has a minimum and maximum, then the range of value of t is
Question 99 :
The function f(x) = x<sup>5</sup> - 5x<sup>4</sup> + 5x<sup>3</sup> - 1 has-
Question 100 :
If f(x) = (cos x + i sin x) (cos 3x + i sin 3x) .... (cos (2n - 1) x + i sin (2n - 1)x), then f′′(x) is equal to -
Question 102 :
If the function f : R → R be defined by f(x) = tan x − x, then f(x)
Question 103 :
If f(x) and g(x) are differentiable functions for 0 ≤ x ≤ 1 such that f(0) = 2, g(0) = 0, f(1) = 6, g(1) = 2, then in the interval (0, 1)
Question 104 :
The distance travelled s(in meteres) by a particle in t second is given by, s = t<sup>3</sup> + 2t<sup>2</sup> + t.The speed of the particle after 18 will be
Question 105 :
If $y = \frac{e^{x} + e^{- x}}{e^{x} - e^{- x}},\ \text{then}\frac{\text{dy}}{\text{dx}}\ \text{is\ equal\ to\ }$
Question 106 :
The equation of the tangent to the curve (1+x<sup>2</sup>)y = 2 − x, where it crosses the x-axis, is
Question 107 :
$\frac{d}{\text{dx}}\left\lbrack \tan^{- 1}\left( \frac{a - x}{1 + \text{ax}} \right) \right\rbrack$is equal to
Question 108 :
The perimeter of a sector is a constant. If its area is to be maximum, the sectorial angle is
Question 109 :
The point P of the curve y<sup>2</sup> = 2x<sup>3</sup> such that the tangent at P is perpendicular to the line 4x − 3y + 2 = 0 is given by
Question 110 :
The function f(x) = acos x + btan x + x has extreme values at x = 0 and $x = \frac{\pi}{6}$, then
Question 111 :
If $x = a\left( 1 + \text{cosθ} \right),\ y = a(\theta + \sin{\theta),\ then\frac{d^{2}y}{dx^{2}}\ at\ \theta = \frac{\pi}{2}\ }\text{is\ }$
Question 112 :
The line (x/a) + (y/b) = 2, touches the curve $\frac{x^{n}}{a^{n}} + \frac{y^{n}}{b^{n}} = 2$, at
Question 113 :
The interval in which the function f(x) = x e<sup>2 − x</sup> increases is
Question 114 :
The value of c in Lagrange’s theorem for the function f(x) = log<sub>e</sub>sin x in the interval [π/6, 5 π/6] is
Question 115 :
If f(x) = x + 2, then f<sup>′</sup>(f(x)) at x = 4, is