Question 2 :
A uniform solid sphere of mass m and radius R is suspended in vertical plane from a point on its periphery.The time period of its oscillation is:
Question 3 :
A body of mass 1 kg is executing S.H.M., its displacement y cm at t seconds is given by y = 6 sin (100t + $\pi$/4). Its maximum kinetic energy is :<br/>
Question 4 :
In the equations below, A, B, $\omega$ and $\phi$ are constants; $y$ and $t$ are variables; $t$ represents time. Only one of the following equations does not represent SHM. Which one is that?
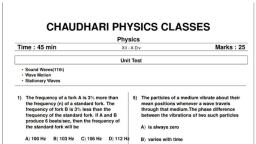
Question 5 :
Find the time period of a periodic motion having frequency as $100Hz$.
Question 6 :
For a particle in SHM the K.E. at any instant is given by K= k $ cos^{2}\omega t $ . The total energy of SHM is
Question 7 :
$mx^{2} - bx + k = 0$. Find time after which to the energy will become half of initial maximum value in damped forced oscillation.
Question 8 :
If the time period of a pendulum is $25 s$. What is the frequency of the pendulum?
Question 10 :
The time period of a particle executing SHM is 2s. After what time interval from t = 0, will its displacement be half the amplitude:
Question 11 :
A particle undergoing SHM has the equation $x = A \sin (\omega t + \phi)$,where x represents the displacement of the particle. The kinetic energy oscillates with time period.
Question 12 :
Equation of SHM is x = 10 sin 10 $\pi$t. Then the time period is, x is in cm and t is in sec
Question 13 :
A particle executes SHM on a straight line. At two positions it's velocity $u$ and $v$ while acceleration, $\alpha$ and $\beta$ respectively $\left[ \beta >\alpha >0 \right]. $ the distance between the these two positions is
Question 14 :
In the case of an oscillating simple pendulum if the air resistance is taken into consideration, then
Question 15 :
A uniform spring has an unstretched length $l$ and a force constant $k$. The spring is cut into two parts of unstretched length ${l}_{1}$ and ${l}_{2}$ such that ${ l }_{ 1 }=\eta { l }_{ 2 }$, where $\eta$ is an integer. The corresponding force constants ${k}_{1}$ and ${k}_{2}$ are
Question 16 :
The displacement of a particle performing linear S.H.M is given by $x=6 sin(3 \pi t-5\pi/6) $ metre. Find the time at which the particle reaches the extreme position towards the left:
Question 17 :
The average kinetic energy of a simple harmonic oscillator is $2$ J and its total energy is $5$ J.Its minimum potential energy is :<br/>
Question 18 :
The minimum phase difference between two SHM's is:<br/>$ y_{1}=\sin \left(\dfrac{\pi}{6}\right) \sin(\omega t)+\sin\left(\dfrac{\pi }{3}\right) \cos(\omega t )$<br/><br/>$ y_{2}=\cos\left(\dfrac{\pi}{6}\right) \sin(\omega t)+\sin \left(\dfrac{\pi}{3}\right) \cos(\omega t)$ is:
Question 19 :
A particle is executing simple harmonic motion with amplitude $A$. When the ratio of its kinetic energy to the potential energy is $\dfrac{1}{4}$, its displacement from its mean position is
Question 20 :
The displacement of a particle executing SHM is given by<br>$y\,=\,5\,\sin \, 4t\,+\,\displaystyle \frac{\pi}{3}$<br>If $T$ is the time period and the mass of the particle is $2$ g, the kinetic energy of the particle when $t\,=\,\displaystyle \frac{T}{4}$ is given by
Question 21 :
Two particles are in S.H.M, of same amplitude 'a', same frequency 'f', along the same straight line about the same mean position. The maximum distance between the two particles is $a \sqrt{2}$. The initial phase difference between the particles is :<br/>
Question 22 :
Using equation $x=Ae^ {{(\displaystyle\frac{-bt}{2m})}} \cos(\omega't+\phi)$ and assuming $\phi = 0$ at $t=0$, find the expression for acceleration at $t=0$.<br/>
Question 23 :
A small solid cylinder of mass M attached to a horizontal massless spring can roll without slipping along a horizontal surface. find its time period.
Question 24 :
A Particle performs linear S.H.M. Starting from the mean position. its amplitude is A and time period is T. At the instance when its speed is half the maximum speed, its displacement x is