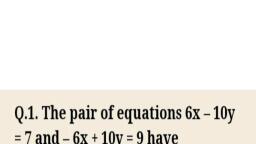Question 1 :
The graph of the linear equation $$2x -y = 4$$ cuts x-axis at
Question 3 :
A member of these family with positive gradient making an angle of$$\frac{\pi }{4}$$ with the line3x-4y=2, is
Question 4 :
If the system of equation, $${a}^{2}x-ay=1-a$$ & $$bx+(3-2b)y=3+a$$ possesses a unique solution $$x=1$$, $$y=1$$ then:
Question 5 :
If $$(a, 3)$$ is the point lying on the graph of the equation $$5x\, +\, 2y\, =\, -4$$, then find $$a$$.
Question 6 :
For what value of k does the system of equations$$\displaystyle 2x+ky=11\:and\:5x-7y=5$$ has no solution?
Question 7 :
The number of pairs of reals (x, y) such that $$x =x^2+y^2$$ and $$y =2xy$$ is
Question 10 :
The unit digit of a number is $$x$$ and its tenth digit is $$y$$ then the number will be 
Question 12 :
What is the equation of straight line passing through the point (4, 3) and making equal intercepts on the coordinate axes ?
Question 14 :
A choir is singing at a festival. On the first night $$12$$ choir members were absent so the choir stood in $$5$$ equal rows. On the second night only $$1$$ member was absent so the choir stood in $$6$$ equal rows. The same member of people stood in each row each night. How many members are in the choir?
Question 16 :
Five tables and eight chairs cost Rs. $$7350$$; three tables and five chairs cost Rs. $$4475$$. The price of a table is
Question 17 :
If $$p+q=1$$ andthe ordered pair (p, q) satisfies $$3x+2y=1$$,then it also satisfies
Question 20 :
The graph of the line $$5x + 3y = 4$$ cuts the $$y$$-axis at the point
Question 21 :
The sum of two numbers is $$2$$ and their difference is $$1$$. Find the numbers.
Question 22 :
Two perpendicular lines are intersecting at $$(4,3)$$. One meeting coordinate axis at $$(4,0)$$, find the coordinates of the intersection of other line with the cordinate axes.
Question 23 :
Let PS be the median of the triangle with vertices $$P\left( 2,2 \right), Q\left( 6,-1 \right), R\left( 7,3 \right).$$The equation of the line passing through $$\left( 1,-1 \right)$$and parallel to PS is
Question 24 :
The value of $$k$$ for which the system of equations $$3x + 5y= 0$$ and $$kx + 10y = 0$$ has a non-zero solution, is ________.
Question 25 :
If $$2x + y = 5$$, then $$4x + 2y$$ is equal to _________.
Question 26 :
What is the equationof Y-axis? Hence, find the point of intersection of Y-axis and the line $$y\,=\, 3x\, +\, 2$$.
Question 27 :
The  linear equation, such that each point on its graph has an ordinate $$3$$ times its abscissa is $$y=mx$$. Then the value of $$m$$ is<br/>
Question 28 :
Some students are divided into two groups A & B. If $$10$$ students are sent from A to B, the number in each is the same. But if $$20$$ students are sent from B to A, the number in A is double the number in B. Find the number of students in each group A & B.<br/>
Question 29 :
A line which passes through (5, 6) and (-3. -4) has an equation of
Question 30 :
The solution of the equation $$2x - 3y = 7$$ and $$4x - 6y = 20$$ is
Question 31 :
The survey of a manufacturing company producing a beverage and snacks was done. It was found that it sells orange drinks at $$ $1.07$$ and choco chip cookies at $$ $0.78$$ the maximum. Now, it was found that it had sold $$57$$ food items in total and earned about $$ $45.87 $$ of revenue. Find out the equations representing these two. 
Question 32 :
State whether the given statement is true or false:The graph of a linear equation in two variables need not be a line.<br/>
Question 33 :
Solve the following equations:<br/>$$x + \dfrac {4}{y} = 1$$,<br/>$$y + \dfrac {4}{x} = 25$$.Then $$(x,y)=$$
Question 34 :
The solution of the simultaneous equations $$\displaystyle \frac{x}{2}+\frac{y}{3}=4\: \: and\: \: x+y=10 $$ is given by
Question 35 :
Equation of a straight line passing through the point $$(2,3)$$ and inclined at an angle of $$\tan^{-1}\dfrac{1}{2}$$ with the line $$y+2x=5$$, is:
Question 37 :
In a zoo there are some pigeons and some rabbits. If their heads are counted these are $$300$$ and if their legs are counted these are $$750$$ How many pigeons are there?
Question 38 :
If (a, 4) lies on the graph of $$3x + y = 10$$, then the value of a is
Question 39 :
The linear equation $$y = 2x + 3$$ cuts the $$y$$-axis at 
Question 40 :
Examine whether the point $$(2, 5)$$ lies on the graph of the equation $$3x\, -\, y\, =\, 1$$.