Page 1 :
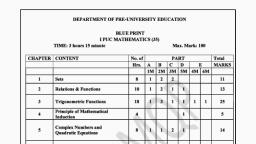
St. Joseph’s Composite P U College Vijayapur, JEE Main Practice Test, , JEE-2023, , Date: 03/01/2022, , Duration: 3:00 Hrs, , Maximum Marks: 300, , General Instructions, 1. The test is of 3 hours duration and the maximum marks are 300., 2. The question paper consists of 3 parts (Part I: Physics, Part II: Chemistry, Part III: Mathematics). Each part has, two sections (Section 1 and Section 2)., 3. Section 1 contains 20 Multiple Choice Questions. Each question has 4 choices. Out of which ONLY ONE, CHOICE is correct., 4. Section 2 contains 10 Numerical Type Questions. Out of which 5 questions need to answer. The answer to, each question is a NUMERICAL VALUE. For each question write the correct numerical value of the answer. If, the answer is a decimal numerical value, than round-off the decimal places, than write., Marking Scheme, 1. Section 1: +4 for correct answer, −1(negative marking) for incorrect answer. 0 For all other cases., 2. Section 2: +4 for correct answer, 0 for all other cases. There is no negative marking., Part I: Physics, Section 1, Section 2, Part II: Chemistry, Section 1, Section 2, Part III: Mathematics, Section 1, 1. In a class of 60 students, 40 opted for NCC, 30 opted for NSS and 20 opted for both NCC and NSS. Find how, many students were opted neither NCC nor NSS?, A. 10, B. 15, C.20, D.25, 2, , 2. Let Z be the set of integers. If A= {𝑥 ∈ 𝑍: 2(𝑥+2)(𝑥 −5𝑥+6) = 1} and B= {𝑥 ∈ 𝑍: −3 < 2𝑥 − 1 < 9}, then the, number of subsets of the set A× 𝐵 is:, A. 215, B.218, C.212, D.210, 3. If X= {4𝑛 − 3𝑛 − 1: 𝑛 ∈ 𝑁} and Y= {9(𝑛 − 1): 𝑛 ∈ 𝑁}, where N is the set of natural numbers, then 𝑋 ∪ 𝑌 is, equal to, A. N, B.𝑌 − 𝑋, C.X, D.Y, 2, 4. x − 3|x| + 2 < 0, then x belongs to, A. (1, 2), B. (−2, −1), C.(−2, −1) ∪ (1, 2), D.(−3, 5), 𝑥/2, 𝑥, 5. If 3, + 2 > 25, then the solution set is, A. R, B.(2, ∞), C.(4, ∞), D. None of these, 𝑥, 6. Domain of 𝑓(𝑥) =, is, 1−|𝑥|, , A. 𝑅 − [−1,1], , B. (−1,1), , C. (−∞, 1) ∪ (0,1), , D. 𝑅 − {−1,1}

Page 2 :
St. Joseph’s Composite P U College Vijayapur, 7. If 𝑛(𝐴) = 2 and total number of possible relations from set A to set B is 1024, then n(B) is, A.10, B. 5, C. 512, D. 20, 2, 2, 8. . Domain of √𝑎 − 𝑥 , (𝑎 > 0) is, A. (−𝑎, 𝑎), B. [−𝑎, 𝑎], C. [0, 𝑎], D. (−𝑎, 0], °, °, 9. √3 csc 20 − sec 20 is equal to, A. 2, B. 3, C.4, D. 1, 10. If tan 𝐴 + cot 𝐴 = 2, then the value of tan4 𝐴 + cot 4 𝐴 is, A. 5, B. 2, C.1, D. 4, °, °, 11. The value of cos 1200 + tan 1485 is, A., , 1, , 3, , B. 2, , 2, , °, , −3, , C., °, , D., , 2, , °, , −1, 2, , °, , 12. The value of tan 1 tan 2 tan 3 … tan 89 is, A. 0, , 1, , B. 1, , C. 2, , D. -1, , 13. 𝑐𝑜𝑠 2 45°- 𝑠𝑖𝑛2 15° =, A., , 1, , √3, 2, , 𝐵. 2, , C. √3 /4, , D., , 1, √3, , 14. If 𝑎 sin3 𝑥 + 𝑏 cos3 𝑥 = sin 𝑥 cos 𝑥 and 𝑎 sin 𝑥 = 𝑏 cos 𝑥 then 𝑎2 + 𝑏2 =, A. 0, B. 1, C. 2, D. 3, 15. Let the orthocenter and centroid of a triangle be A (−3, 5) and 𝐵(3, 3) respectively. If C is the circumcentre, of this triangle, then the radius of the circle having line segment AC as diameter, is:, A., , 3√5, 2, , B.√10, , C.2√10, , D.3√, , 5, 2, , 16. Suppose that the points (ℎ, 𝑘), (1, 2)𝑎𝑛𝑑 (−3, 4) lie on the line 𝐿1 .If a line 𝐿2 passing through the points, 𝑘, , (ℎ, 𝑘) 𝑎𝑛𝑑 (4, 3) is perpendicular on 𝐿1 , then equals:, ℎ, A., , 1, , B.0, , 3, , C. 3, , D.−, , 1, 7, , 17. Two vertices of a triangle are (0, 2) and (4, 3). If its orthocenter is at the origin, then its third vertex lies in, which quadrant?, A. Third, B. Second, C. First D. Fourth, 18. If the vertices of a triangle are (2, 5), (3, 9) 𝑎𝑛𝑑 (−4, 0), then find the equation of the altitude through (2, 5), A. 7𝑥 + 9𝑦 − 59 = 0, B.9𝑥 + 7𝑦 − 59 = 0, C. 7𝑥 + 9𝑦 − 95 = 0, , D. 9𝑥 + 7𝑦 − 95 = 0, 3, , 19. Lines are drawn parallel to the line4𝑥 − 3𝑦 + 2 = 0, at a distance 5 units from the origin. Then which one of, the following points lies on any of these lines?, 1, , 2, , 1, , 1, , 1, , 1, , 1, , 2, , 4, , 3, , 4, , 3, , 4, , 3, , 4, , 3, , A. {− , } B. { , − } C. { , } D. {− , − }, 20. Two sides of a triangle are2𝑥 − 𝑦 = 0 𝑎𝑛𝑑 𝑥 + 𝑦 = 3. If the centroid of the triangle is (2, 3) then find its, third side., A. 𝑥 − 5𝑦 = 9, B. 5𝑥 − 𝑦 = 9, C. 𝑥 − 5𝑦 = −9, , D. 5𝑥 − 𝑦 = −9, , Section 2, 21., 22., 23., 24., , Sets A and B have 3 and 6 elements respectively. What can be minimum number of elements in A∪B?, If 𝐴 = {1, 2, 3, 4, 5, 6}, then the number of subsets of A which contain at least two elements is, The value of sin 1200 cos 1500 + cos 2400 sin 3300 =, 𝑡𝑎𝑛18 + 𝑡𝑎𝑛27 + 𝑡𝑎𝑛18𝑡𝑎𝑛27 =

Page 3 :
St. Joseph’s Composite P U College Vijayapur, 25. A rectangle is described in a circle with a diameter lying along the line 3𝑦 = 𝑥 + 7. If the two adjacent, vertices of the rectangle are (−8, 5) 𝑎𝑛𝑑 (6, 5), then the area of the rectangle (in sq. units) is:, 26. Two points (𝑎, 3) 𝑎𝑛𝑑 (5, 𝑏) are the opposite vertices of a rectangle. If the other two vertices lie on the line, 𝑦 = 2𝑥 + 𝑐 which passes through the point (𝑎, 𝑏) then value of c is – 𝑘, where 𝑘 = _______, 27. The number of real solutions of the equation log 0.8 𝑥 = |𝑥|, 𝑖𝑠, 28. In a class of 140 students numbered 1 to 140, all even numbered is students opted Mathematics course, those, whose number is divisible by 3 opted Physics course and those whose number is divisible by 5 opted, Chemistry course. Then the number of students who did not opt for any of the three course is:, 29. Two finite sets have m and n elements. The total number of subsets of the first set is 56 more than the total, number of subsets of the second set. The values of 𝑚 + 𝑛 𝑖𝑠, 30. In a class of 35 students, 17 have taken Mathematics, 10 have taken Mathematics but not Economics. If each, student has taken either Mathematics or Economics or both, then the number of students who have taken, Economics but not Mathematics is