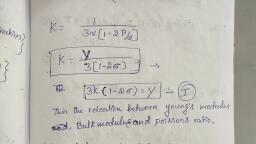Page 1 :
Course: USO1CPHY01, UNIT -1 ELASTICITY - I, “+ Introduction:, , If the distance between any two points in a body remains invariable, the body is, said to be a rigid body. In practice it is not possible to have a perfectly rigid body. The, deformations are, , (i) There may be change in length, , (ii) There is a change of volume but no change in shape, , (iii) There is a change in shape with no change in volume, , All bodies get deformed under the action of force. The size and shape of the body, will change on application of force. There is a tendency of body to recover its original, size and shape on removal of this force., , Elasticity: The property of a material body to regain its original condition on the, removal of deforming forces, is called elasticity. Quartz fibre is considered to be the, perfectly elastic body., , Plasticity: The bodies which do not show any tendency to recover their original, condition on the removal of deforming forces are called plasticity. Putty is considered to, be the perfectly plastic body., , Load: The load is the combination of external forces acting on a body and its effect is to, change the form or the dimensions of the body. Any kind of deforming force is known as, Load., , When a body is subjected to a force or a system of forces it undergoes a change in, size or shape or both. Elastic bodies offer appreciable resistance to the deforming, forces. As a result, work has to be done to deform them. This amount of work is stored, in body as elastic potential energy. When the deforming force is removed, its increased, elastic potential energy produced a tendency in the body to restore the body to its, original state of zero energy or stable equilibrium. This tendency is due to the internal, forces which come into play by the deformation., , Stress: When a force is applied on a body, there will be relative displacement of the, particles. Due to the property of elasticity the particles tend to regain their original, position. The restoring or recovering force per unit area set up inside the body is called, stress., , e The stress is measured in terms of the load or the force applied per unit, area. Hence its units are dynes/cm? in CGS and Newton/m? in MKS., ¢ Ithas adimension [ML1T-]. It is same as that of pressure., , There are two types of stress., (1) Normal Stress: Restoring force per unit area perpendicular to the surface is called, normal stress., , Page 1 of 16
Page 2 :
(2) Tangential or Shearing Stress: Restoring force per unit area parallel to the surface, is called tangential or shearing stress., , Strain: The unit change produced in the dimensions of a body under a system of forces, in equilibrium, is called strain. The strain being ratio. It has no unit., , There are following three types of strains., (1) Longitudinal or Linear Strain: It is defined as the increase in length per, unit original length of an object when the it is deformed by an external force., The ratio of change in length to the original length is called longitudinal or, elongation strain., Change in length (1), Original length (L), It is also called Elongation strain or Tensile strain., , i.e. Longitudinal or Linear Strain =, , (2) Volume Strain: It is defined as change in volume per unit original volume,, when an object is deformed by the external force., The ratio of change in volume to the original volume is called volume, strain., , | . Change in volume (v), i.e. Volume Strain = ————_____—_, Original volume (V), , (3) Shear strain: When the force applied is acting parallel to the surface of the, body then the change takes place only in the shape of the body. The, corresponding strain is called shear strain., , The angular deformation produced by an external force is called shear, strain., , Characteristics of a Perfectly Elastic Material, If a body is perfectly elastic then, ¢ Strain is always same for a given stress., e Strain vanishes completely when the deforming force is removed., e For maintaining the strain, the stress is constant., , ** Hooke’s law, This fundamental law of elasticity was proposed by Robert Hooke in 1679 and it, states that “Provided the strain is small, the stress is directly proportional to the strain’. In, other words, the ratio of stress to strain is a constant quantity for the given material and, itis called the modulus of elasticity or coefficient of elasticity., Stress « Strain, , « Stress = E x Strain, Stress, , , , ~ Strain, The units and dimensions of the modulus of elasticity are the same as that of, stress., , “+ Elastic Limit:, , When the stress is continually increased in the case of solid, a point is reached at, which the strain increased more rapidly. The stress at which the linear relationship, between stress and strain hold good is called elastic limit of the material., , Page 2 of 16
Page 3 :
“> Stress-Strain Diagram:, , %, ts, , STRESS, , ¢ The direct proportionality between, stress and strain is found to be true only for, small values of strain as shown in the figure., , ¢ The portion OA of the curve is a, straight line showing that the stress is directly, proportional to strain. It shows that Hooke’s, law is strictly obeyed up to the value of stress, corresponding to point A. This point is called, Elastic limit., , ¢ Beyond point A, the curve is not a, straight line. In this region AB, the strain, increases more rapidly than the stress and the, behavior is partly elastic and partly plastic. If, the object is unloaded at B, it does not come, back to its original condition along path AO,, but takes the dotted path BC. The object is said, to have acquired permanent set. And OC is called the residual strain., Beyond the point B, the length of the wire starts increasing without any increase, in stress. Thus, wire begins to flow after point B and it continues up to D. The, point B, at which the wire begins to flow is called yield point., Beyond the point F, the graph indicates that length of the wire increases, even if, the wire is unloaded. The wire breaks ultimately at point E, called the breaking, point of the wire. The portion of the graph between D and E is called the plastic, region., , "PLASTIC !, RANGE", , "ELASTIC, LIMIT", , ', 1, ', I, ', ‘, 1, 1, ', 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, ', 1, 1, ', , , , Three types of elasticity:, , There are three types of strain, therefore we have three types of elasticity., , (1) Linear elasticity called Young’s modulus, corresponding to linear strain., , (2) Elasticity of volume or Bulk modulus, corresponding to volume strain., , (3) Elasticity of shape or shear modulus or Modulus of Rigidity, corresponding to, , shear strain., , (1) Young’s Modulus:, , When the deforming force is applied to the body only along a particular, direction, the change per unit length in that direction is called longitudinal, linear, or elongation strain., The force applied per unit area of cross section is called longitudinal or linear, stress., The ratio of longitudinal stress to linear strain, within the elastic limit, is called, Young's modulus., It is denoted by Y, Longitudinal stress, , ~ Linear strain, Consider a wire of length L having area of cross section ‘a’, fixed at one end and, loaded at the other end., Suppose that a normal force F is applied to the free end of the wire and its length, increase by I., , F l, Longitudinal stress =— and linear strain = L, a, , Page 3 of 16
Page 4 :
FL, or Y=—, al, , Young's modulus can also be defined as the force applied to a wire of unit length, and unit cross sectional area to produce the increase in length by unity., The units of Young’s modulus are Pascal or N/m? in MKS and dyne/cm2 in CGS, , system., , (2) Bulk Modulus:, It is defined as the ratio of the normal stress to the volume strain., , It is denoted by K. The bulk modulus is also known as the coefficient of cubical, elasticity., , Normal stress, , ~ Volume strain, Consider a cubic of volume V and surface area ‘a’. Suppose that a force F which, , ., acts uniformly over the whole surface of the cubic, produces a decrease in its, volume by v then,, F . v, Normal stress = — and volume strain = 7, FV, , av, , 5 F, Now, the pressureis P= a, , —PV, «= K =—, v, e Ifthe volume increase on increasing the stress the bulk modulus given by, PV, K=—, v, , The units of bulk modulus are Pa or N/m? in SI., Compressibility: The reciprocal of the bulk modulus of a material is called, , compressibility i.e. 1/K., , (3) Modulus of Rigidity:, e Itis defined as the ratio of tangential stress to shear strain., , ¢ Itis also called shear modulus. It is denoted by n., _ Tangential stress, , Shear strain, , qd bb e Consider a rectangular block, whose, lower face aDCc is fixed and the upper, face ABbd is subjected to tangential force, , i F, lef ¢ Let ‘a’ be the area of the each face and AD, c, , , , , , = L be the perpendicular distance, , between them., e The tangential force will displace the, a upper face of parallelepiped by a distance, AA’ = 1., Page 4 of 16
Page 5 :
e If ZADA' = 6, then @ is the angle of shear., , Tangential stress = a and Shear strain = Angle of shear =@, F, -G@if, 6 aé, ¢ For solids, angle of shear is very small, so in ADAA’, Gmetanbi= AA _ l, * fan" D, e The distance ‘I’ through which the upper face has been displaced is called lateral, displacement., . FL, nT, , + Work done per unit volume in case of elongation strain:, ¢ Consider a wire of length / and area of cross section ‘a’ suspended from a rigid, , , , , , support., e Suppose that a normal force ‘F’ is applied at its free end and its length increases, by dl., e The work done for a small displacement dl is given by, dW =Fdl wi(L), e We know that,, E, =, y=], L, Yal, oP, Substituting this value of F in above equation (1), we get, aw ="** al, e Therefore, the total work done for the stretching a wire of length ‘I’ given by,, l, W= | dw, oO, l, Wien Yal al, ~ | L, 0, l, w= "fia, “oL, 0, W = Ya(l?, LAD, 1 Yal, Ww= 2, ; xl, W=-Fx\], 2, , 1, «. Total work done W = z straching force x change in length, , ¢ This work done stored in form of potential energy., , Page 5 of 16